中考备考专题复习:探索规律问题
试卷更新日期:2017-02-08 类型:二轮复习
一、单选题
-
1.
下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有4个小圆圈,第②个图形中一共有10个小圆圈,第③个图形中一共有19个小圆圈,…,按此规律排列,则第⑦个图形中小圆圈的个数为( )
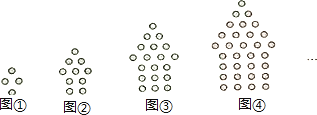 A、64 B、77 C、80 D、852.
A、64 B、77 C、80 D、852.观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,…,按此规律,图形⑧中星星的颗数是( )
 A、43 B、45 C、51 D、533.
A、43 B、45 C、51 D、533.如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )
 A、y=2n+1 B、y=2n+n C、y=2n+1+n D、y=2n+n+14.
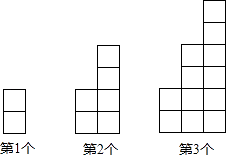
A、y=2n+1 B、y=2n+n C、y=2n+1+n D、y=2n+n+14.用大小相等的小正方形按一定规律拼成下列图形,则第n个图形中小正方形的个数是( )
 A、2n+1 B、n2﹣1 C、n2+2n D、5n﹣25.
A、2n+1 B、n2﹣1 C、n2+2n D、5n﹣25.如图,用黑白两种颜色的菱形纸片,按黑色纸片数逐渐增加1的规律拼成下列图案,若第n个图案中有2017个白色纸片,则n的值为( )
 A、671 B、672 C、673 D、6746. 我们根据指数运算,得出了一种新的运算,如表是两种运算对应关系的一组实例:
A、671 B、672 C、673 D、6746. 我们根据指数运算,得出了一种新的运算,如表是两种运算对应关系的一组实例:指数运算
21=2
22=4
23=8
…
31=3
32=9
33=27
…
新运算
log22=1
log24=2
log28=3
…
log33=1
log39=2
log327=3
…
根据上表规律,某同学写出了三个式子:①log216=4,②log525=5,③log2 =﹣1.其中正确的是( )
A、①② B、①③ C、②③ D、①②③7. 如图,正方形ABCD的边长为2,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …,按照此规律继续下去,则S9的值为( )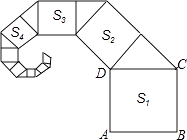 A、( )6 B、( )7 C、( )6 D、( )7
A、( )6 B、( )7 C、( )6 D、( )7二、填空题
-
8.
下列图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒,…,按此规律,图案⑦需根火柴棒.
 9. 按一定规律排列的一列数: ,1,1,□, , , ,…请你仔细观察,按照此规律方框内的数字应为 .
9. 按一定规律排列的一列数: ,1,1,□, , , ,…请你仔细观察,按照此规律方框内的数字应为 .
10.如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长,P1 , P2 , P3 , …,均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,﹣1),P5(﹣1,﹣1),P6(﹣1,2)…根据这个规律,点P2016的坐标为 .
 11.
11.将一些半径相同的小圆按如图所示的规律摆放,请仔细观察,第n个图形有个小圆•(用含n的代数式表示)
 12.
12.如图,下面每个图形中的四个数都是按相同的规律填写的,根据此规律确定x的值为 .
 13. 观察下列各式的规律:
13. 观察下列各式的规律:(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4
…
可得到(a﹣b)(a2016+a2015b+…+ab2015+b2016)=
14. 观察下列数据:﹣2, ,﹣ , ,﹣ ,…,它们是按一定规律排列的,依照此规律,第11个数据是 .
15.找出下列各图形中数的规律,依此,a的值为 .
 16.
16.如图是小强用铜币摆放的4个图案,根据摆放图案的规律,试猜想第n个图案需要个铜币.
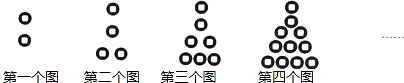 17.
17.小李用围棋子排成下列一组有规律的图案,其中第1个图案有1枚棋子,第2个图案有3枚棋子,第3个图案有4枚棋子,第4个图案有6枚棋子,…,那么第9个图案的棋子数是枚.
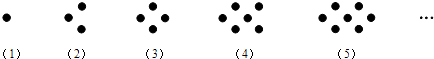 18.
18.如图,每个图案都由大小相同的正方形组成,按照此规律,第n个图案中这样的正方形的总个数可用含n的代数式表示为 .
 19.
19.如图,下列各图形中的三个数之间均具有相同的规律,依此规律,那么第4个图形中的x= , 一般地,用含有m,n的代数式表示y,即y= .
 20. 等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 .
20. 等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 . 21. 如图,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴交直线y= x于点B1 , 以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1 , 再过点C1作A2B2∥y轴,分别交直线y=x和y= x于A2 , B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为(用含正整数n的代数式表示)
21. 如图,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴交直线y= x于点B1 , 以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1 , 再过点C1作A2B2∥y轴,分别交直线y=x和y= x于A2 , B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为(用含正整数n的代数式表示)
三、综合题
-
22.
环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度y与时间x成反比例关系.
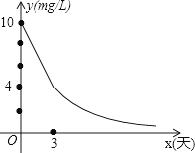 (1)、求整改过程中硫化物的浓度y与时间x的函数表达式;(2)、该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0mg/L?为什么?23.
(1)、求整改过程中硫化物的浓度y与时间x的函数表达式;(2)、该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0mg/L?为什么?23.【操作发现】在计算器上输入一个正数,不断地按“ ”键求算术平方根,运算结果越来越接近1或都等于1.
【提出问题】输入一个实数,不断地进行“乘以常数k,再加上常数b”的运算,有什么规律?
【分析问题】我们可用框图表示这种运算过程(如图a).
也可用图象描述:如图1,在x轴上表示出x1 , 先在直线y=kx+b上确定点(x1 , y1),再在直线y=x上确定纵坐标为y1的点(x2 , y1),然后再x轴上确定对应的数x2 , …,以此类推.
【解决问题】研究输入实数x1时,随着运算次数n的不断增加,运算结果x,怎样变化.
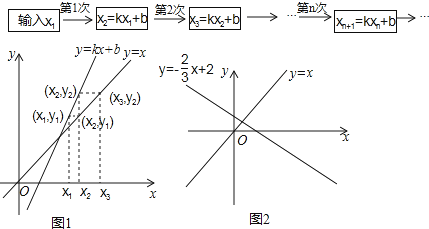 (1)、若k=2,b=﹣4,得到什么结论?可以输入特殊的数如3,4,5进行观察研究;(2)、若k>1,又得到什么结论?请说明理由;(3)、①若k=﹣ ,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2 , x3 , x4 , 并写出研究结论;
(1)、若k=2,b=﹣4,得到什么结论?可以输入特殊的数如3,4,5进行观察研究;(2)、若k>1,又得到什么结论?请说明理由;(3)、①若k=﹣ ,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2 , x3 , x4 , 并写出研究结论;②若输入实数x1时,运算结果xn互不相等,且越来越接近常数m,直接写出k的取值范围及m的值(用含k,b的代数式表示)
24. 有一列按一定顺序和规律排列的数:第一个数是 ;
第二个数是 ;
第三个数是 ;
…
对任何正整数n,第n个数与第(n+1)个数的和等于 .
(1)、经过探究,我们发现:设这列数的第5个数为a,那么 , , ,哪个正确?
请你直接写出正确的结论;
(2)、请你观察第1个数、第2个数、第3个数,猜想这列数的第n个数(即用正整数n表示第n数),并且证明你的猜想满足“第n个数与第(n+1)个数的和等于 ”;(3)、设M表示 , , ,…, ,这2016个数的和,即 ,求证: .
25.已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x
…
1
2
3
5
7
9
…
y
…
1.98
3.95
2.63
1.58
1.13
0.88
…
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
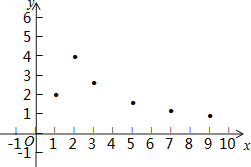 (1)、如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;(2)、根据画出的函数图象,写出:
(1)、如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;(2)、根据画出的函数图象,写出:①x=4对应的函数值y约为
②该函数的一条性质: