中考备考专题复习：概率及其求法

试卷更新日期：2017-02-08 类型：二轮复习

进入出卷网下载

一、单选题

1. 下列说法正确的是（　　）

A、为了审核书稿中的错别字，选择抽样调查 B、为了了解春节联欢晚会的收视率，选择全面调查 C、“射击运动员射击一次，命中靶心”是随机事件 D、“经过由交通信号灯的路口，遇到红灯”是必然事件

查看试题解析
2. 一个不透明布袋里装有1个白球、2个黑球、3个红球，它们除颜色外均相同．从中任意摸出一个球，则是红球的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
3. 质地均匀的骰子六个面分别刻有1到6的点数，掷两次骰子，得到向上一面的两个点数，则下列事件中，发生可能性最大的是（　　）

A、点数都是偶数 B、点数的和为奇数 C、点数的和小于13 D、点数的和小于2

查看试题解析
4. 从分别标有数﹣3，﹣2，﹣1，0，1，2，3的七张没有明显差别的卡片中，随机抽取一张，所抽卡片上的数的绝对值不小于2的概率是（　　）

A、 $\frac{1}{7}$ B、 $\frac{2}{7}$ C、 $\frac{3}{7}$ D、 $\frac{4}{7}$

查看试题解析
5. 下列说法正确的是（　　）

A、“任意画一个三角形，其内角和为360°”是随机事件 B、已知某篮球运动员投篮投中的概率为0.6，则他投十次可投中6次 C、抽样调查选取样本时，所选样本可按自己的喜好选取 D、检测某城市的空气质量，采用抽样调查法

查看试题解析
6.
如图，△ABC是一块绿化带，将阴影部分修建为花圃，已知AB=15，AC=9，BC=12，阴影部分是△ABC的内切圆，一只自由飞翔的小鸟将随机落在这块绿化带上，则小鸟落在花圃上的概率为（　　）

A、 $\frac{1}{6}$ B、 $\frac{π}{6}$ C、 $\frac{π}{8}$ D、 $\frac{π}{5}$

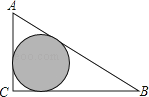查看试题解析
7. 下列说法中正确的是（　　）

A、“打开电视，正在播放《新闻联播》”是必然事件 B、“x²＜0（x是实数）”是随机事件 C、掷一枚质地均匀的硬币10次，可能有5次正面向上 D、为了了解夏季冷饮市场上冰淇淋的质量情况，宜采用普查方式调查

查看试题解析
8. 掷一枚质地均匀的硬币10次，下列说法正确的是（　　）

A、每2次必有1次正面向上 B、必有5次正面向上 C、可能有7次正面向上 D、不可能有10次正面向上

查看试题解析
9. 下列算式
① $\sqrt{9}$ =±3；② ${(- \frac{1}{3})}^{- 2}$ =9；③2⁶÷2³=4；④ $\sqrt{{(- 2016)}^{2}}$ =2016；⑤a+a=a² ．
运算结果正确的概率是（　　）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
10. 一枚质地均匀的骰子，其六个面上分别标有数字1，2，3，4，5，6，投掷一次，朝上一面的数字是偶数的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
11. 一个不透明的口袋中有四个完全相同的小球，把它们分别标号为1，2，3，4随机摸出一个小球，不放回，再随机摸出一个小球，两次摸出的小球标号的积小于4的概率是（　　）

A、 $\frac{1}{6}$ B、 $\frac{5}{16}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析

二、填空题

12. 有5张看上去无差别的卡片，上面分别写着0，π， $\sqrt{2}$ ， $\frac{1}{9}$ ，1.333．随机抽取1张，则取出的数是无理数的概率是．

查看试题解析
13.
如图所示的六边形广场由若干个大小完全相同的黑色和白色正三角形组成，一只小鸟在广场上随机停留，刚好落在黑色三角形区域的概率为．

查看试题解析
14.
如图，随机地闭合开关S₁ ， S₂ ， S₃ ， S₄ ， S₅中的三个，能够使灯泡L₁ ， L₂同时发光的概率是．

查看试题解析
15. 任取不等式组 ${\begin{cases} k - 3 \leq 0 \\ 2 k + 5 > 0 \end{cases}$ 的一个整数解，则能使关于x的方程：2x+k=﹣1的解为非负数的概率为．

查看试题解析
16.
小球在如图所示的地板上自由滚动，并随机停留在某块正方形的地砖上，则它停在白色地砖上的概率是．

查看试题解析
17. 一个不透明的口袋里装有若干除颜色外其他完全相同的小球，其中有6个黄球，将口袋中的球摇匀，从中任意摸出一个球记下颜色后再放回，通过大量重复上述实验后发现，摸到黄球的频率稳定在30%，由此估计口袋中共有小球个．

查看试题解析
18. 一个不透明的袋中装有除颜色外均相同的8个黑球、4个白球和若干个红球．每次摇匀后随机摸出一个球，记下颜色后再放回袋中，通过大量重复摸球试验后，发现摸到红球的频率稳定于0.4，由此可估计袋中约有红球个．

查看试题解析
19. 从“线段，等边三角形，圆，矩形，正六边形”这五个圆形中任取一个，取到既是轴对称图形又是中心对称图形的概率是．

查看试题解析
20. 在1，π， $\sqrt{3}$ ，2，﹣3.2这五个数中随机取出一个数，则取出的这个数大于2的概率是．

查看试题解析
21. 林业部门要考察某种幼树在一定条件下的移植成活率，下表是这种幼树在移植过程中的一组数据：
移植的棵数n
1000
1500
2500
4000
8000
15000
20000
30000
成活的棵数m
865
1356
2220
3500
7056
13170
17580
26430
成活的频率 $\frac{m}{n}$
0.865
0.904
0.888
0.875
0.882
0.878
0.879
0.881
估计该种幼树在此条件下移植成活的概率为．

查看试题解析
22. 不透明袋子中装有6个球，其中有1个红球、2个绿球和3个黑球，这些球除颜色外无其他差别，从袋子中随机取出1个球，则它是绿球的概率是．

查看试题解析
23. 已知一包糖果共有5种颜色（糖果只有颜色差别），如图是这包糖果分布百分比的统计图，在这包糖果中任意取一粒，则取出糖果的颜色为绿色或棕色的概率是．

查看试题解析
24. 如图，一只蚂蚁在正方形ABCD区域内爬行，点O是对角线的交点，∠MON=90°，OM，ON分别交线段AB，BC于M，N两点，则蚂蚁停留在阴影区域的概率为．

查看试题解析
25. 某种油菜籽在相同条件下发芽试验的结果如表：
每批粒数n
100
300
400
600
1000
2000
3000
发芽的频数m
96
284
380
571
948
1902
2848
发芽的频率 $\frac{m}{n}$
0.960
0.947
0.950
0.952
0.948
0.951
0.949
那么这种油菜籽发芽的概率是（结果精确到0.01）．

查看试题解析

三、综合题

26. 甲、乙两人进行摸牌游戏．现有三张形状大小完全相同的牌，正面分别标有数字2，3，5．将三张牌背面朝上，洗匀后放在桌子上．

(1)、甲从中随机抽取一张牌，记录数字后放回洗匀，乙再随机抽取一张．请用列表法或画树状图的方法，求两人抽取相同数字的概率；

(2)、若两人抽取的数字和为2的倍数，则甲获胜；若抽取的数字和为5的倍数，则乙获胜．这个游戏公平吗？请用概率的知识加以解释．

查看试题解析
27. 锐锐参加我市电视台组织的“牡丹杯”智力竞答节目，答对最后两道单选题就顺利通关，第一道单选题有3个选项，第二道单选题有4个选项，这两道题锐锐都不会，不过锐锐还有两个“求助”可以用（使用“求助”一次可以让主持人去掉其中一题的一个错误选项）．

(1)、如果锐锐两次“求助”都在第一道题中使用，那么锐锐通关的概率是．

(2)、如果锐锐两次“求助”都在第二道题中使用，那么锐锐通关的概率是．

(3)、如果锐锐将每道题各用一次“求助”，请用树状图或者列表来分析他顺序通关的概率．

查看试题解析
28. 为了解学生的体能情况，随机选取了1000名学生进行调查，并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况，整理成以下统计表，其中“√”表示喜欢，“×”表示不喜欢．
项目
学生
长跑
短跑
跳绳
跳远
200
√
×
√
√
300
×
√
×
√
150
√
√
√
×
200
√
×
√
×
150
√
×
×
×

(1)、估计学生同时喜欢短跑和跳绳的概率；

(2)、估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率；

(3)、如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大？

查看试题解析
29.
在一个不透明的布袋中装有三个小球，小球上分别标有数字﹣1、0、2，它们除了数字不同外，其他都完全相同．

(1)、随机地从布袋中摸出一个小球，则摸出的球为标有数字2的小球的概率为；

(2)、小丽先从布袋中随机摸出一个小球，记下数字作为平面直角坐标系内点M的横坐标．再将此球放回、搅匀，然后由小华再从布袋中随机摸出一个小球，记下数字作为平面直角坐标系内点M的纵坐标，请用树状图或表格列出点M所有可能的坐标，并求出点M落在如图所示的正方形网格内（包括边界）的概率．

查看试题解析
30.
国家规定，中小学生每天在校体育活动时间不低于1小时，为了解这项政策的落实情况，有关部门就“你某天在校体育活动时间是多少”的问题，在某校随机抽查了部分学生，再根据活动时间t（小时）进行分组（A组：t＜0.5，B组：0.5≤t≤1，C组：1≤t＜1.5，D组：t≥1.5），绘制成如下两幅不完整统计图，请根据图中信息回答问题：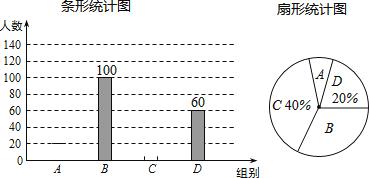

(1)、此次抽查的学生数为人；

(2)、补全条形统计图；

(3)、从抽查的学生中随机询问一名学生，该生当天在校体育活动时间低于1小时的概率是

(4)、若当天在校学生数为1200人，请估计在当天达到国家规定体育活动时间的学生有人．

查看试题解析
31. 在平面直角坐标系中，把横纵坐标都是整数的点称为“整点”．

(1)、直接写出函数y= $\frac{3}{x}$ 图象上的所有“整点”A₁ ， A₂ ， A₃ ， …的坐标；

(2)、在（1）的所有整点中任取两点，用树状图或列表法求出这两点关于原点对称的概率．

查看试题解析

移植的棵数n	1000	1500	2500	4000	8000	15000	20000	30000
成活的棵数m	865	1356	2220	3500	7056	13170	17580	26430
成活的频率 $\frac{m}{n}$	0.865	0.904	0.888	0.875	0.882	0.878	0.879	0.881

每批粒数n	100	300	400	600	1000	2000	3000
发芽的频数m	96	284	380	571	948	1902	2848
发芽的频率 $\frac{m}{n}$	0.960	0.947	0.950	0.952	0.948	0.951	0.949

项目学生	长跑	短跑	跳绳	跳远
200	√	×	√	√
300	×	√	×	√
150	√	√	√	×
200	√	×	√	×
150	√	×	×	×