中考备考专题复习:锐角三角函数
试卷更新日期:2017-02-08 类型:二轮复习
一、单选题
-
1. 一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( )
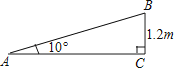 A、斜坡AB的坡度是10° B、斜坡AB的坡度是tan10° C、AC=1.2tan10°米 D、AB= 米2. 一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
A、斜坡AB的坡度是10° B、斜坡AB的坡度是tan10° C、AC=1.2tan10°米 D、AB= 米2. 一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( ) A、 米2 B、 米2 C、(4+ )米2 D、(4+4tanθ)米23.
A、 米2 B、 米2 C、(4+ )米2 D、(4+4tanθ)米23.如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )
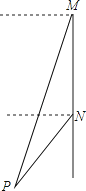 A、22.48 B、41.68 C、43.16 D、55.634. 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1: ,则大楼AB的高度约为( )(精确到0.1米,参考数据: ≈1.41, ≈1.73, ≈2.45)
A、22.48 B、41.68 C、43.16 D、55.634. 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1: ,则大楼AB的高度约为( )(精确到0.1米,参考数据: ≈1.41, ≈1.73, ≈2.45)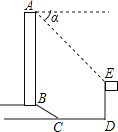 A、30.6 B、32.1 C、37.9 D、39.45. 聊城“水城之眼”摩天轮是亚洲三大摩天轮之一,也是全球首座建筑与摩天轮相结合的城市地标,如图,点O是摩天轮的圆心,长为110米的AB是其垂直地面的直径,小莹在地面C点处利用测角仪测得摩天轮的最高点A的仰角为33°,测得圆心O的仰角为21°,则小莹所在C点到直径AB所在直线的距离约为(tan33°≈0.65,tan21°≈0.38)( )
A、30.6 B、32.1 C、37.9 D、39.45. 聊城“水城之眼”摩天轮是亚洲三大摩天轮之一,也是全球首座建筑与摩天轮相结合的城市地标,如图,点O是摩天轮的圆心,长为110米的AB是其垂直地面的直径,小莹在地面C点处利用测角仪测得摩天轮的最高点A的仰角为33°,测得圆心O的仰角为21°,则小莹所在C点到直径AB所在直线的距离约为(tan33°≈0.65,tan21°≈0.38)( ) A、169米 B、204米 C、240米 D、407米6.
A、169米 B、204米 C、240米 D、407米6.如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )
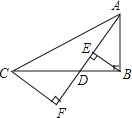 A、不变 B、增大 C、减小 D、先变大再变小7. 如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A、不变 B、增大 C、减小 D、先变大再变小7. 如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )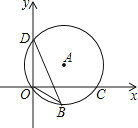 A、 B、 C、 D、8. 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
A、 B、 C、 D、8. 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )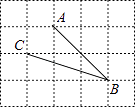 A、2 B、 C、 D、9. 如图,在△ABC中,∠B=90°,tan∠C= ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
A、2 B、 C、 D、9. 如图,在△ABC中,∠B=90°,tan∠C= ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )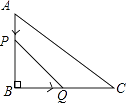 A、18cm2 B、12cm2 C、9cm2 D、3cm210. 如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )
A、18cm2 B、12cm2 C、9cm2 D、3cm210. 如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )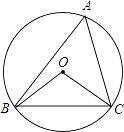 A、3 B、4 C、5 D、611. 已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )A、 B、 C、 D、212. 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
A、3 B、4 C、5 D、611. 已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )A、 B、 C、 D、212. 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( ) A、 B、 C、 D、13. 如图,某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘正在南海巡航的渔政船前往救援,当飞机到达海面3000m的高空C处时,测得A处渔政船的俯角为45°,测得B处发生险情渔船的俯角为30°,此时渔政船和渔船的距离AB是( )
A、 B、 C、 D、13. 如图,某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘正在南海巡航的渔政船前往救援,当飞机到达海面3000m的高空C处时,测得A处渔政船的俯角为45°,测得B处发生险情渔船的俯角为30°,此时渔政船和渔船的距离AB是( )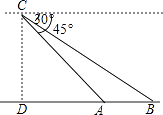 A、3000 m B、3000( +1)m C、3000( -1)m D、1500 m14. 济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计, ≈1.7,结果精确到1m,则该楼的高度CD为( )
A、3000 m B、3000( +1)m C、3000( -1)m D、1500 m14. 济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计, ≈1.7,结果精确到1m,则该楼的高度CD为( )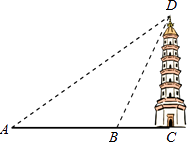 A、47m B、51m C、53m D、54m15. 小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )
A、47m B、51m C、53m D、54m15. 小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )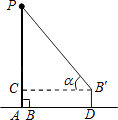 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
16. 请从以下两个小题中任选一个作答,若多选,则按第一题计分.
A.一个多边形的一个外角为45°,则这个正多边形的边数是 .
B.运用科学计算器计算:3 sin73°52′≈ . (结果精确到0.1)
17. 已知∠AOB=60°,点P是∠AOB的平分线OC上的动点,点M在边OA上,且OM=4,则点P到点M与到边OA的距离之和的最小值是 .
18. 如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ= ,那么当点P运动一周时,点Q运动的总路程为 .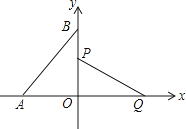 19. 如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为
19. 如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为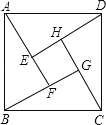
20. 如图,在矩形ABCD中,AD=10,CD=6,E是CD边上一点,沿AE折叠△ADE,使点D恰好落在BC边上的F处,M是AF的中点,连接BM,则sin∠ABM= .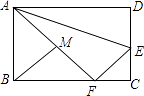
三、计算题
-
21. 计算:( )﹣1+(sin60°﹣1)0﹣2cos30°+| ﹣1|
四、综合题
-
22. 如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,OC=1,以点O为圆心OC为半径作半圆.
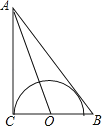 (1)、求证:AB为⊙O的切线;
(1)、求证:AB为⊙O的切线;
(2)、如果tan∠CAO= ,求cosB的值.23. 如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(5,0),菱形OABC的顶点B,C都在第一象限,tan∠AOC= ,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG. (1)、求点B的坐标.(2)、当OG=4时,求AG的长.(3)、求证:GA平分∠OGE.(4)、连结BD并延长交x轴于点P,当点P的坐标为(12,0)时,求点G的坐标.24. 如图,已知AB为半圆O的直径,C为半圆O上一点,连接AC,BC,过点O作OD⊥AC于点D,过点A作半圆O的切线交OD的延长线于点E,连接BD并延长交AE于点F.
(1)、求点B的坐标.(2)、当OG=4时,求AG的长.(3)、求证:GA平分∠OGE.(4)、连结BD并延长交x轴于点P,当点P的坐标为(12,0)时,求点G的坐标.24. 如图,已知AB为半圆O的直径,C为半圆O上一点,连接AC,BC,过点O作OD⊥AC于点D,过点A作半圆O的切线交OD的延长线于点E,连接BD并延长交AE于点F. (1)、求证:AE•BC=AD•AB;(2)、若半圆O的直径为10,sin∠BAC= ,求AF的长.25. 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)、求证:AE•BC=AD•AB;(2)、若半圆O的直径为10,sin∠BAC= ,求AF的长.25. 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.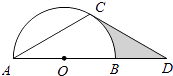 (1)、求证:CD是⊙O的切线;(2)、若⊙O的半径为2,求图中阴影部分的面积.26. 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(0,﹣ ),C(2,0),其对称轴与x轴交于点D
(1)、求证:CD是⊙O的切线;(2)、若⊙O的半径为2,求图中阴影部分的面积.26. 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(0,﹣ ),C(2,0),其对称轴与x轴交于点D (1)、求二次函数的表达式及其顶点坐标;(2)、若P为y轴上的一个动点,连接PD,则 PB+PD的最小值为;(3)、M(x,t)为抛物线对称轴上一动点
(1)、求二次函数的表达式及其顶点坐标;(2)、若P为y轴上的一个动点,连接PD,则 PB+PD的最小值为;(3)、M(x,t)为抛物线对称轴上一动点
①若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,则这样的点N共有 个;
②连接MA,MB,若∠AMB不小于60°,求t的取值范围.
-