中考备考专题复习:相似与位似
试卷更新日期:2017-02-08 类型:二轮复习
一、单选题
-
1. 下列各组线段长度成比例的是( )A、1cm、2cm、3cm、4cm B、1cm、3cm、4.5cm、6.5cm C、1.1cm、2.2cm、3.3cm、4.4cm D、1cm、2cm、2cm、4cm2. 如图,点C是线段AB的黄金分割点(AC>BC),下列结论错误的是( )
 A、 B、BC2=AB•BC C、= D、≈0.6183. 设(2y﹣z):(z+2x):y=1:5:2,则(3y﹣z):(2z﹣x):(x+3y)=( )A、1:5:7 B、3:5:7 C、3:5:8 D、2:5:84. 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的 , 那么点B′的坐标是( )
A、 B、BC2=AB•BC C、= D、≈0.6183. 设(2y﹣z):(z+2x):y=1:5:2,则(3y﹣z):(2z﹣x):(x+3y)=( )A、1:5:7 B、3:5:7 C、3:5:8 D、2:5:84. 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的 , 那么点B′的坐标是( ) A、(-2,3) B、(2,-3) C、(3,-2)或(-2,3) D、(-2,3)或(2,-3)5. 已知k= , 且+n2+9=6n,则关于自变量x的一次函数y=kx+m+n的图象一定经过第( )象限.A、一、二 B、二、三 C、三、四 D、一、四6. 在△ABC中,AB=AC=1,BC=x,∠A=36°.则的值为( )A、 B、 C、1 D、7. 线段AB=10cm,点C是线段AB的黄金分割点,且AC>BC,则AC与AB的关系是( )A、AC=AB B、AC=AB C、AC=AB D、AC=AB8. 如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于( )
A、(-2,3) B、(2,-3) C、(3,-2)或(-2,3) D、(-2,3)或(2,-3)5. 已知k= , 且+n2+9=6n,则关于自变量x的一次函数y=kx+m+n的图象一定经过第( )象限.A、一、二 B、二、三 C、三、四 D、一、四6. 在△ABC中,AB=AC=1,BC=x,∠A=36°.则的值为( )A、 B、 C、1 D、7. 线段AB=10cm,点C是线段AB的黄金分割点,且AC>BC,则AC与AB的关系是( )A、AC=AB B、AC=AB C、AC=AB D、AC=AB8. 如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于( )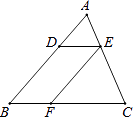 A、5:8 B、3:8 C、3:5 D、2:59. 在△ABC中,AB=12,BC=18,CA=24,另一个和它相似的△DEF最长的一边是36,则△DEF最短的一边是( )A、72 B、18 C、12 D、2010.
A、5:8 B、3:8 C、3:5 D、2:59. 在△ABC中,AB=12,BC=18,CA=24,另一个和它相似的△DEF最长的一边是36,则△DEF最短的一边是( )A、72 B、18 C、12 D、2010.如图,在5×5的正方形方格中,△ABC的顶点都在边长为1的小正方形的顶点上,作一个与△ABC相似的△DEF , 使它的三个顶点都在小正方形的顶点上,则△DEF的最大面积是( ).
 A、5 B、10 C、 D、11. 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
A、5 B、10 C、 D、11. 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )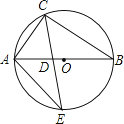 A、1: B、1: C、1:2 D、2:312. 如图的矩形ABCD中,E点在CD上,且AE<AC.若P、Q两点分别在AD、AE上,AP:PD=4:1,AQ:QE=4:1,直线PQ交AC于R点,且Q、R两点到CD的距离分别为q、r,则下列关系何者正确?( )
A、1: B、1: C、1:2 D、2:312. 如图的矩形ABCD中,E点在CD上,且AE<AC.若P、Q两点分别在AD、AE上,AP:PD=4:1,AQ:QE=4:1,直线PQ交AC于R点,且Q、R两点到CD的距离分别为q、r,则下列关系何者正确?( ) A、q<r,QE=RC B、q<r,QE<RC C、q=r,QE=RC D、q=r,QE<RC
A、q<r,QE=RC B、q<r,QE<RC C、q=r,QE=RC D、q=r,QE<RC二、填空题
-
13. 已知△ABC∽△DEF,∠A=∠D,∠C=∠F且AB:DE=1:2,则EF:BC= .14. △ABC中,∠A=90°,AB=AC , BC=63cm,现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示,已知剪得的纸条中有一张是正方形,则这张正方形纸条是从下往上数第张.
 15. 如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,2 ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为
15. 如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,2 ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为
16. 如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有(写出所有正确结论的序号)①△CMP∽△BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2 ;
⑤当△ABP≌△ADN时,BP=4 ﹣4.
 17. 如图,反比例函数y= (k≠0)的图象经过A,B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为2,则k的值为 .
17. 如图,反比例函数y= (k≠0)的图象经过A,B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为2,则k的值为 .
三、作图题
-
18.
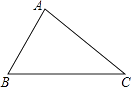
如图,已知△ABC,∠BAC=90°,请用尺规过点A作一条直线,使其将△ABC分成两个相似的三角形(保留作图痕迹,不写作法)
四、解答题
-
19.
已知:如图,△ABC∽△ADE , ∠A=45°,∠C=40°.求:∠ADE的度数.
 20. 如图,点D、E分别在△ABC的边AB、AC上,且AB=9,AC=6,AD=3,若使△ADE与△ABC相似,求AE的长.
20. 如图,点D、E分别在△ABC的边AB、AC上,且AB=9,AC=6,AD=3,若使△ADE与△ABC相似,求AE的长. 21. 如图,已知△ABC.只用直尺(没有刻度的尺)和圆规,求作一个△DEF,使得△DEF∽△ABC,且EF=BC.(要求保留作图痕迹,不必写出作法)
21. 如图,已知△ABC.只用直尺(没有刻度的尺)和圆规,求作一个△DEF,使得△DEF∽△ABC,且EF=BC.(要求保留作图痕迹,不必写出作法) 22. 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,﹣4),B(3,﹣2),C(6,﹣3).
22. 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,﹣4),B(3,﹣2),C(6,﹣3).(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2 , 使△A2B2C2与△A1B1C1的相似比为2:1;
(3)若每一个方格的面积为1,则△A2B2C2的面积为 .

五、综合题
-
23. 尤秀同学遇到了这样一个问题:如图1所示,已知AF,BE是△ABC的中线,且AF⊥BE,垂足为P,设BC=a,AC=b,AB=c.
求证:a2+b2=5c2
该同学仔细分析后,得到如下解题思路:
先连接EF,利用EF为△ABC的中位线得到△EPF∽△BPA,故 ,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证
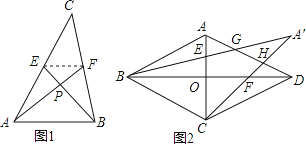 (1)、请你根据以上解题思路帮尤秀同学写出证明过程.(2)、利用题中的结论,解答下列问题:在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图2所示,求MG2+MH2的值.
(1)、请你根据以上解题思路帮尤秀同学写出证明过程.(2)、利用题中的结论,解答下列问题:在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图2所示,求MG2+MH2的值. 24. 如图1,在直角坐标系xOy中,直线l:y=kx+b交x轴,y轴于点E,F,点B的坐标是(2,2),过点B分别作x轴、y轴的垂线,垂足为A、C,点D是线段CO上的动点,以BD为对称轴,作与△BCD或轴对称的△BC′D.
24. 如图1,在直角坐标系xOy中,直线l:y=kx+b交x轴,y轴于点E,F,点B的坐标是(2,2),过点B分别作x轴、y轴的垂线,垂足为A、C,点D是线段CO上的动点,以BD为对称轴,作与△BCD或轴对称的△BC′D.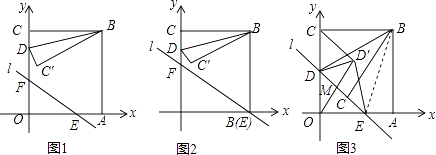 (1)、当∠CBD=15°时,求点C′的坐标.(2)、当图1中的直线l经过点A,且k=﹣ 时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.(3)、当图1中的直线l经过点D,C′时(如图3),以DE为对称轴,作于△DOE或轴对称的△DO′E,连结O′C,O′O,问是否存在点D,使得△DO′E与△CO′O相似?若存在,求出k、b的值;若不存在,请说明理由.
(1)、当∠CBD=15°时,求点C′的坐标.(2)、当图1中的直线l经过点A,且k=﹣ 时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.(3)、当图1中的直线l经过点D,C′时(如图3),以DE为对称轴,作于△DOE或轴对称的△DO′E,连结O′C,O′O,问是否存在点D,使得△DO′E与△CO′O相似?若存在,求出k、b的值;若不存在,请说明理由.
-