中考备考专题复习：圆的有关性质
试卷更新日期：2017-02-08 类型：二轮复习
一、单选题
-
1. 下列语句中，正确的是 （ ）A、长度相等的弧是等弧 B、在同一平面上的三点确定一个圆 C、三角形的内心是三角形三边垂直平分线的交点 D、三角形的外心到三角形三个顶点的距离相等2. 下列说法：
①三点确定一个圆；
②垂直于弦的直径平分弦；
③三角形的内心到三条边的距离相等；
④圆的切线垂直于经过切点的半径．
其中正确的个数是（ ）
A、0 B、2 C、3 D、43.如图，将半径为6的⊙O沿AB折叠，弧AB与AB垂直的半径OC交于点D且CD=2OD，则折痕AB的长为（ ）
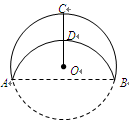A、 B、 C、6 D、4.如图，已知以直角梯形ABCD的腰CD为直径的半圆O与梯形的上底AD、下底BC以及腰AB均相切，切点分别是D、C、E．若半圆O的半径为2，梯形的腰AB为5，则该梯形的周长是（ ）.
A、9 B、10 C、12 D、145.如图，⊙O中，弦AB与CD交于点M，∠A=45°，∠AMD=75°，则∠B的度数是（ ）
A、15° B、25° C、30° D、75°6.如图，△ABC内接于⊙O，AB是⊙O的直径，∠B=30°，CE平分∠ACB交⊙O于E，交AB于点D，连接AE，则S△ADE：S△CDB的值等于（ ）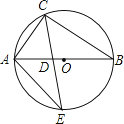
A、1： B、1： C、1：2 D、2：37.如图，四边形ABCD内接于⊙O，F是 上一点，且 = ，连接CF并延长交AD的延长线于点E，连接AC．若∠ABC=105°，∠BAC=25°，则∠E的度数为（ ）
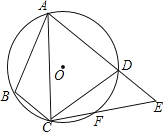A、45° B、50° C、55° D、60°8.把一张圆形纸片按如图所示方式折叠两次后展开，图中的虚线表示折痕，则 的度数是（ ）
A、120° B、135° C、150° D、165°9.如图，四边形ABCD内接于⊙O，若四边形ABCO是平行四边形，则∠ADC的大小为（ ）
A、45° B、50° C、60° D、75°10. 如图，BD是⊙O的直径，点A、C在⊙O上，
= 
，∠AOB=60°，则∠BDC的度数是（ ） 
A、60° B、45° C、35° D、30°11. 如图，直线AB，AD与⊙O相切于点B，D，C为⊙O上一点，且∠BCD=140°，则∠A的度数是（ ）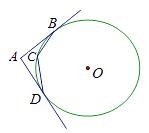
A、70° B、105° C、100° D、110°12. 如图，小敏家厨房一墙角处有一自来水管，装修时为了美观，准备用木板从AB处将水管密封起来，互相垂直的两墙面与水管分别相切于D，E两点，经测量AD=10cm，BE=15cm，则该自来水管的半径为（ ）cm．
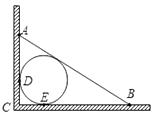A、5 B、10 C、6 D、8二、填空题
-
13.
如图，四边形ABCD为⊙O的内接四边形，已知∠BCD=110°，则∠BAD=度．
14.如图，△ABC是⊙O的内接正三角形，⊙O的半径为3，则图中阴影部分的面积是 ．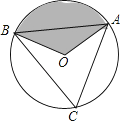
15. 如图，AB是半圆O的直径，C是半圆O上一点，弦AD平分∠BAC，交BC于点E，若AB=6，AD=5，则DE的长为 ．
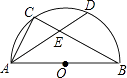16.如图，⊙O的弦AB、CD相交于点E，若CE：BE=2：3，则AE：DE=
17. 如图1，小敏利用课余时间制作了一个脸盆架，图2是它的截面图，垂直放置的脸盆与架子的交点为A，B，AB=40cm，脸盆的最低点C到AB的距离为10cm，则该脸盆的半径为 cm．
三、解答题
-
18.
已知点P到圆的最大距离为11，最小距离为7，则此圆的半径为多少？
19. 一条排水管的截面如图所示．已知排水管的半径OB=10，水面宽AB=16．求截面圆心O到水面的距离．
四、综合题
-
20.
如图，⊙O是△ABC的外接圆，AC为直径，弦BD=BA，BE⊥DC交DC的延长线于点E．
(1)、求证：∠1=∠BAD；(2)、求证：BE是⊙O的切线．21. 如图，已知四边形ABCD内接于圆O，连结BD，∠BAD=105°，∠DBC=75°．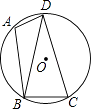
(1)、求证：BD=CD；(2)、若圆O的半径为3，求
的长． 22.如图1，2，3分别以△ABC的AB和AC为边向△ABC外作正三角形（等边三角形）、正四边形（正方形）、正五边形，BE和CD相交于点O．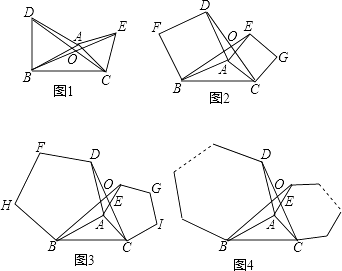
(1)、在图1中，求证：△ABE≌△ADC．(2)、由（1）证得△ABE≌△ADC，由此可推得在图1中∠BOC=120°，请你探索在图2中，∠BOC的度数，并说明理由或写出证明过程．(3)、填空：在上述（1）（2）的基础上可得在图3中∠BOC=（填写度数）．(4)、由此推广到一般情形（如图4），分别以△ABC的AB和AC为边向△ABC外作正n边形，BE和CD仍相交于点O，猜想得∠BOC的度数为（用含n的式子表示）．