中考备考专题复习:矩形、菱形、正方形
试卷更新日期:2017-02-08 类型:二轮复习
一、单选题
-
1. 下列命题中,正确的命题是( )A、两条对角线相等的四边形是矩形 B、两条角线互相垂直且相等的四边形是正方形 C、两条对角线相互垂直的四边形是菱形 D、两条对角线互相平分的四边形是平行四边形2. 平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-3,0)、B(0,2)、C(3,0)、D(0,-2),四边形ABCD是( ).A、矩形 B、菱形 C、正方形 D、梯形3.
如图,在梯形ABCD中,AD//BC, ∠B=70°∠C=40°,DE//AB交BC于点E.若AD=3,BC=10,则CD的长是( )
 A、7 B、10 C、13 D、144. 如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )
A、7 B、10 C、13 D、144. 如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )
A、2 B、2.4 C、2.6 D、35. 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD⊥DC,BD=DC,CE平分∠BCD,交AB于点E,交BD于点H,EN∥DC交BD于点N.下列结论:
①BH=DH;②CH=(+1)EH;③= . 其中正确的是( ) A、①② B、②③ C、①③ D、①②③6. 如图所示,四边形ABCD是梯形,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,则tanB=( )
A、①② B、②③ C、①③ D、①②③6. 如图所示,四边形ABCD是梯形,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,则tanB=( ) A、2 B、2 C、 D、7. 如图,在△ABC中,AD平分∠BAC , 按如下步骤作图:
A、2 B、2 C、 D、7. 如图,在△ABC中,AD平分∠BAC , 按如下步骤作图:第一步,分别以点A、D为圆心,以大于 AD的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF .
若BD=6,AF=4,CD=3,则BE的长是( ).
 A、2 B、4 C、6 D、88.
A、2 B、4 C、6 D、88.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D , 交AB于点E , 且BE=BF , 添加一个条件,仍不能证明四边形BECF为正方形的是( ).
 A、BC=AC B、CF⊥BF C、BD=DF D、AC=BF9.
A、BC=AC B、CF⊥BF C、BD=DF D、AC=BF9.如图,正方形ABCD的对角线交于点O , 以AD为边向外作Rt△ADE , ∠AED=90°,连接OE , DE=6,OE= ,则另一直角边AE的长为( ).
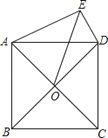 A、 B、2 C、8 D、1010. 在矩形ABCD中,AB=1,AD= ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )
A、 B、2 C、8 D、1010. 在矩形ABCD中,AB=1,AD= ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )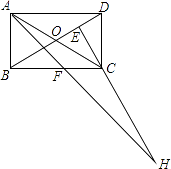 A、②③ B、③④ C、①②④ D、②③④11. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
A、②③ B、③④ C、①②④ D、②③④11. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,
其中正确的结论的个数是( )
 A、1 B、2 C、3 D、412. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )
A、1 B、2 C、3 D、412. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )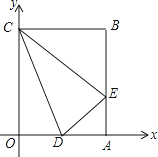 A、(3,1) B、(3, ) C、(3, ) D、(3,2)
A、(3,1) B、(3, ) C、(3, ) D、(3,2)二、填空题
-
13. 已知梯形的上底长为a , 中位线长为m , 那么这个梯形的下底长为.14. 如图,在等腰梯形ABCD中,AC⊥BD,AC=6cm,则等腰梯形ABCD的面积为cm2 .
 15. 如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是 .
15. 如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是 . 16. 如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为 .
16. 如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为 . 17. 如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.
17. 如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.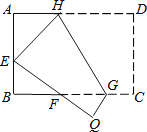
三、解答题
-
18.
已知:如图,△ABC中,∠ABC=90°,BD是∠ABC的平分线,DE⊥AB于点E , DF⊥BC于点F . 求证:四边形DEBF是正方形.
 19.
19.如图,四边形ABCD中,AB∥CD,AB≠CD,BD=AC.
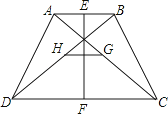 (1)、求证:AD=BC;(2)、
(1)、求证:AD=BC;(2)、若E、F、G、H分别是AB、CD、AC、BD的中点,求证:线段EF与线段GH互相垂直平分.

四、综合题
-
20. 如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.
 (1)、求证:AC2=CD•BC;(2)、过E作EG⊥AB,并延长EG至点K,使EK=EB.
(1)、求证:AC2=CD•BC;(2)、过E作EG⊥AB,并延长EG至点K,使EK=EB.①若点H是点D关于AC的对称点,点F为AC的中点,求证:FH⊥GH;
②若∠B=30°,求证:四边形AKEC是菱形.
21. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.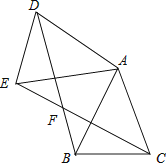 (1)、求证:△AEC≌△ADB;(2)、若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.22. 如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF.
(1)、求证:△AEC≌△ADB;(2)、若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.22. 如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF.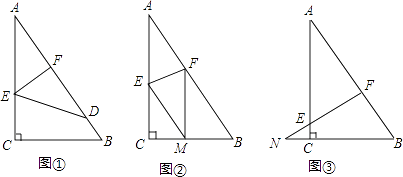 (1)、图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF , 求AE的长;(2)、如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
(1)、图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF , 求AE的长;(2)、如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)、如图③,若FE的延长线与BC的延长线交于点N,CN=1,CE= ,求 的值.