中考备考专题复习：多边形与平行四边形

试卷更新日期：2017-02-08 类型：二轮复习

进入出卷网下载

一、单选题

1. 下列说法正确的是（）

A、同位角相等 B、过一点有且只有一条直线与已知直线平行 C、过一点有且只有一条直线与已知直线垂直 D、只用一种图形进行镶嵌，三角形、四边形、六边形都可以镶嵌

查看试题解析
2. 下列正多边形中，绕其中心旋转72°后，能和自身重合的是（）

A、正方形 B、正五边形 C、正六边形 D、正八边形

查看试题解析
3. 下列图形中，不能镶嵌成平面图案的是 ( )

A、正三角形 B、正四边形 C、正五边形 D、正六边形

查看试题解析
4. 梯形ABCD中，AD∥BC，AB=CD=AD=2，∠B=60°，则下底BC的长是( )

A、 $3$ B、 $4$ C、 $2 \sqrt{3}$ D、 $2 + 2 \sqrt{3}$

查看试题解析
5.
如图，在梯形ABCD中，AD//BC， ∠B=70°∠C=40°，DE//AB交BC于点E．若AD=3，BC=10，则CD的长是( )

A、7 B、10 C、13 D、14

查看试题解析
6.
如图，AB∥CD∥EF，BC∥AD，AC为∠BAD的平分线，图中与∠AOE相等（不含∠AOE）的角有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
7. 正六边形的边心距为 $\sqrt{3}$ ，这个正六边形的面积为（）

A、2 $\sqrt{3}$ B、4 $\sqrt{3}$ C、6 $\sqrt{3}$ D、12

查看试题解析
8. 把边长相等的正五边形ABGHI和正六边形ABCDEF的AB边重合，按照如图的方式叠合在一起，连接EB，交HI于点K，则∠BKI的大小为（　　）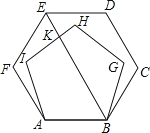

A、90° B、84° C、72° D、88°

查看试题解析
9.
如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若BF=6，AB=5，则AE的长为（　　）

A、4 B、6 C、8 D、10

查看试题解析
10.
如图，在五边形ABCDE中，AB=AC=AD=AE，且AB∥ED，∠EAB=120°，则∠DCB=（　　）

A、150° B、160° C、130° D、60°

查看试题解析
11. 小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（）

A、①，② B、①，④ C、③，④ D、②，③

查看试题解析
12.
如图，在平面直角坐标系中，以O（0，0）、A（1，-1）、B（2，0）为顶点，构造平行四边形，下列各点中不能作为平行四边形第四个顶点坐标的是（　　　）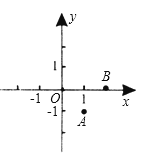

A、（3，-1） B、（-1，-1） C、（1，1） D、（-2，-1）

查看试题解析

二、填空题

13. 正多边形的一个外角是72°，则这个多边形的内角和的度数是．

查看试题解析
14. 现有一个正六边形的纸片，该纸片的边长为20cm，张萌想用一张圆形纸片将该正六边形纸片完全覆盖住，则圆形纸片的直径不能小于 cm．

查看试题解析
15.
如图，已知四边形ABCD中，∠C=72°，∠D=81°．沿EF折叠四边形，使点A、B分别落在四边形内部的点A′、B′处，则∠1+∠2=°．

查看试题解析
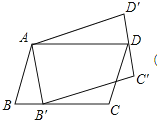
16.
如图，平行四边形ABCD绕点A逆时针旋转30°，得到平行四边形AB′C′D′（点B′与点B是对应点，点C′与点C是对应点，点D′与点D是对应点），点B′恰好落在BC边上，则∠C=

查看试题解析
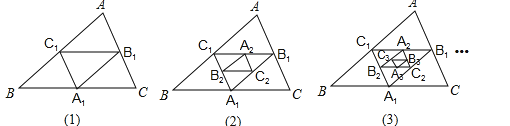
17.
如图，在图（1）中，A₁、B₁、C₁分别是△ABC的边BC、CA、AB的中点，在图（2）中，A₂、B₂、C₂分别是△A₁B₁C₁的边B₁C₁、C₁A₁、A₁B₁的中点，…，按此规律，则第n个图形中平行四边形的个数共有个

查看试题解析

三、综合题

18.
如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．

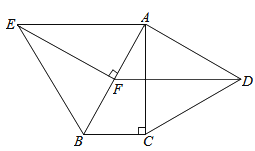(1)、试说明AC=EF；

(2)、求证：四边形ADFE是平行四边形.

查看试题解析
19.
如图，已知抛物线y=﹣ $\frac{1}{4}$ x²﹣ $\frac{1}{2}$ x+2与x轴交于A、B两点，与y轴交于点C

(1)、求点A，B，C的坐标；

(2)、点E是此抛物线上的点，点F是其对称轴上的点，求以A，B，E，F为顶点的平行四边形的面积；

(3)、此抛物线的对称轴上是否存在点M，使得△ACM是等腰三角形？若存在，请求出点M的坐标；若不存在，请说明理由．

查看试题解析
20.
如图1，A，B分别在射线OA，ON上，且∠MON为钝角，现以线段OA，OB为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP，△OBQ，点C，D，E分别是OA，OB，AB的中点．

(1)、求证：△PCE≌△EDQ；

(2)、延长PC，QD交于点R．
①如图1，若∠MON=150°，求证：△ABR为等边三角形；
②如图3，若△ARB∽△PEQ，求∠MON大小和 $\frac{A B}{P Q}$ 的值．

查看试题解析
21.
如图，矩形ABCD中，点E为BC上一点，F为DE的中点，且∠BFC=90°．

(1)、当E为BC中点时，求证：△BCF≌△DEC；

(2)、当BE=2EC时，求 $\frac{C D}{B C}$ 的值；

(3)、设CE=1，BE=n，作点C关于DE的对称点C′，连结FC′，AF，若点C′到AF的距离是 $\frac{2 \sqrt{10}}{5}$ ，求n的值．

查看试题解析
22.
如图，将正n边形绕点A顺时针旋转60°后，发现旋转前后两图形有另一交点O，连接AO，我们称AO为“叠弦”；再将“叠弦”AO所在的直线绕点A逆时针旋转60°后，交旋转前的图形于点P，连接PO，我们称∠OAB为“叠弦角”，△AOP为“叠弦三角形”．
【探究证明】

(1)、请在图1和图2中选择其中一个证明：“叠弦三角形”（△AOP）是等边三角形；

(2)、如图2，求证：∠OAB=∠OAE′．

(3)、图1、图2中的“叠弦角”的度数分别为，；

(4)、图n中，“叠弦三角形”等边三角形（填“是”或“不是”）

(5)、图n中，“叠弦角”的度数为（用含n的式子表示）

查看试题解析