中考备考专题复习：等腰三角形

试卷更新日期：2017-02-08 类型：二轮复习

进入出卷网下载

一、单选题

1. 已知等腰三角形一腰上的高线等于腰长的一半，那么这个等腰三角形的一个底角等于（）

A、15°或75° B、15^° C、75^° D、150°和30°

查看试题解析
2.
如图，CD是Rt△ABC斜边AB上的高，将△BCD 沿 CD折叠，B点恰好落在AB的中点E处，则∠A等于（）

A、25 B、30 C、45 D、60

查看试题解析
3.
如图所示，A是斜边长为m的等腰直角三角形，B ， C ， D都是正方形。则A，B，C，D的面积的和等于 ( )

A、 $\frac{9}{4} m^{2}$ B、 $\frac{5}{2} m^{2}$ C、 $\frac{11}{4} m^{2}$ D、 $3 m^{2}$

查看试题解析
4.
如图，在△ABC中，AB＝6，AC＝8，BC＝10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为( )

A、2 B、2.4 C、2.6 D、3

查看试题解析
5.
如图，是一个三级台阶，它的每一级的长、宽、高分别为20dm、3dm、2dm ， A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点的最短路程是（）

A、15 dm B、20dm C、25dm D、30dm

查看试题解析
6.
如图，△ABC的周长为26，点D，E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P，若BC=10，则PQ的长为（）

A、 $\frac{3}{2}$ B、 $\frac{5}{2}$ C、3 D、4

查看试题解析
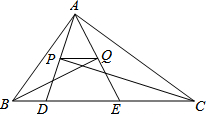7.
直线l₁∥l₂∥l₃ ，且l₁与l₂的距离为1，l₂与l₃的距离为3，把一块含有45°角的直角三角形如图放置，顶点A，B，C恰好分别落在三条直线上，AC与直线l₂交于点D，则线段BD的长度为(　　)

A、 $\frac{25}{4}$ B、 $\frac{25}{3}$ C、 $\frac{20}{3}$ D、 $\frac{15}{4}$

查看试题解析
8. 如图，△ABC中，∠C=90°，∠ABC=60°，BD平分∠ABC ，若AD=6，则CD是（）

A、1 B、2 C、3 D、4

查看试题解析
9.
在矩形ABCD中，AB＝1，AD＝ $\sqrt{3}$ ，AF平分∠DAB，过C点作CE⊥BD于E，延长AF.EC交于点H，下列结论中：①AF＝FH；②BO＝BF；③CA＝CH；④BE＝3ED．正确的是（　　）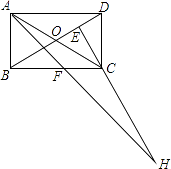

A、②③ B、③④ C、①②④ D、②③④

查看试题解析
10.
如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=50°，则∠CDE的度数为（　　）

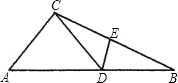A、50° B、51° C、51.5° D、52.5°

查看试题解析
11.
如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：
①AC=FG；②S_△_FAB：S_四边形_CBFG=1：2；③∠ABC=∠ABF；④AD²=FQ•AC，
其中正确的结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
12. 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图，它是由四个全等的直角三角形和中间的小正方形拼成的大正方形，如图所示，如果大正方形的面积是13，小正方形的面积为1，直角三角形的较短直角边长为a，较长直角边长为b，那么（a+b）²的值为（）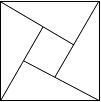

A、13 B、19 C、25 D、169

查看试题解析

二、填空题

13. 矩形的两条对角线的夹角为60°，一条对角线与短边的和为15，则短边的长是，对角线的长是．

查看试题解析
14.
如图，边长为1的菱形ABCD的两个顶点B、C恰好落在扇形AEF的弧EF上．若∠BAD=120°，则弧BC的长度等于 .

查看试题解析
15.
如图，在正方形ABCD外作等腰直角△CDE，DE=CE，连接BE，则tan∠EBC= ．

查看试题解析
16. 如图，AB是半圆O的直径，C是半圆O上一点，弦AD平分∠BAC，交BC于点E，若AB=6，AD=5，则DE的长为．

查看试题解析
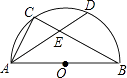17.
如图，将矩形ABCD沿GH对折，点C落在Q处，点D落在E处，EQ与BC相交于F．若AD=8cm，AB=6cm，AE=4cm．则△EBF的周长是cm．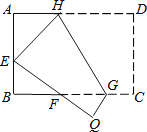

查看试题解析

三、解答题

18.
如图，在直角△ABC中，∠C＝90°，∠CAB的平分线AD交BC于D，若DE垂直平分AB，求∠B的度数．

查看试题解析
19. 如图，△ABC中，∠BAC=90°，AB=AC，O为BC的中点，点E，D分别为边AB，AC上的点，且满足OE⊥OD，求证：OE=OD．

查看试题解析

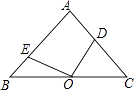
四、综合题

20.
如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．

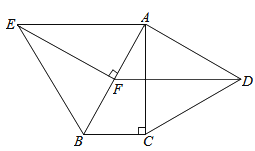(1)、试说明AC=EF；

(2)、求证：四边形ADFE是平行四边形.

查看试题解析
21.
如图，矩形ABCD中，点E为BC上一点，F为DE的中点，且∠BFC=90°．

(1)、当E为BC中点时，求证：△BCF≌△DEC；

(2)、当BE=2EC时，求 $\frac{C D}{B C}$ 的值；

(3)、设CE=1，BE=n，作点C关于DE的对称点C′，连结FC′，AF，若点C′到AF的距离是 $\frac{2 \sqrt{10}}{5}$ ，求n的值．

查看试题解析
22.
如图1，在正方形ABCD内作∠EAF=45°，AE交BC于点E，AF交CD于点F，连接EF，过点A作AH⊥EF，垂足为H．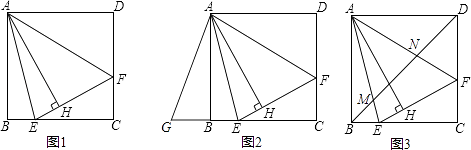

(1)、如图2，将△ADF绕点A顺时针旋转90°得到△ABG．
①求证：△AGE≌△AFE；
②若BE=2，DF=3，求AH的长．

(2)、如图3，连接BD交AE于点M，交AF于点N．请探究并猜想：线段BM，MN，ND之间有什么数量关系？并说明理由．

查看试题解析
23.
在平面直角坐标系中，O为原点，点A（4，0），点B（0，3），把△ABO绕点B逆时针旋转，得△A′BO′，点A，O旋转后的对应点为A′，O′，记旋转角为α．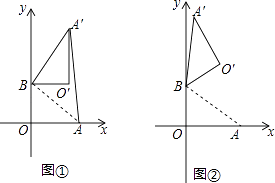

(1)、如图①，若α=90°，求AA′的长；

(2)、如图②，若α=120°，求点O′的坐标；

(3)、在（2）的条件下，边OA上的一点P旋转后的对应点为P′，当O′P+BP′取得最小值时，求点P′的坐标（直接写出结果即可）

查看试题解析
24.
如图，在矩形ABCD中，点O为坐标原点，点B的坐标为（4，3），点A、C在坐标轴上，点P在BC边上，直线l₁：y=2x+3，直线l₂：y=2x﹣3．

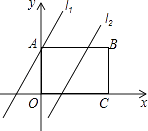(1)、分别求直线l₁与x轴，直线l₂与AB的交点坐标；

(2)、已知点M在第一象限，且是直线l₂上的点，若△APM是等腰直角三角形，求点M的坐标；

(3)、我们把直线l₁和直线l₂上的点所组成的图形为图形F．已知矩形ANPQ的顶点N在图形F上，Q是坐标平面内的点，且N点的横坐标为x，请直接写出x的取值范围（不用说明理由）．

查看试题解析