中考备考专题复习：全等三角形

试卷更新日期：2017-02-08 类型：二轮复习

进入出卷网下载

一、单选题

1.
下图中，全等的图形有（）

A、2组 B、3组 C、4组 D、5组

查看试题解析
2. 使两个直角三角形全等的条件是（）

A、一锐角对应相等 B、两锐角对应相等 C、一条边对应相等 D、两条直角边对应相等

查看试题解析
3. 下列说法错误的是（）

A、等腰三角形两腰上的中线相等 B、等腰三角形两腰上的高线相等 C、等腰三角形的中线与高重合 D、等腰三角形底边的中线上任一点到两腰的距离相等

查看试题解析
4.
如图，某同学把一块三角形的玻璃打破成了三块，现在他要到玻璃店去配一块完全一样形状的玻璃，那么最省事的办法是带（）去配．

A、① B、② C、③ D、①和②

查看试题解析
5. 长为1的一根绳，恰好可围成两个全等三角形，则其中一个三角形的最长边x的取值范围为（　　）

A、 $\frac{l}{6} \leq x < \frac{l}{4}$ B、 $\frac{l}{8} \leq x < \frac{l}{4}$ C、 $\frac{l}{6} < x < \frac{l}{4}$ D、 $\frac{l}{8} < x < \frac{l}{4}$

查看试题解析
6. 已知等腰三角形一腰上的高线等于腰长的一半，那么这个等腰三角形的一个底角等于（）

A、15°或75° B、15^° C、75^° D、150°和30°

查看试题解析
7.
如图，x的值可能为（）

A、10 B、9 C、7 D、6

查看试题解析
8. 如图，△ABC中，AB=AC ， EB=EC ，则由“SSS”可以判定（　　）

A、△ABD≌△ACD B、△ABE≌△ACE C、△BDE≌△CDE D、以上答案都不对

查看试题解析
9. 如果线段AB=3cm，BC=1cm，那么A、C两点的距离d的长度为（　　）

A、4cm B、2cm C、4cm或2cm D、小于或等于4cm，且大于或等于2cm

查看试题解析
10.
如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=50°，则∠CDE的度数为（　　）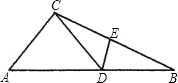

A、50° B、51° C、51.5° D、52.5°

查看试题解析
11.
如图，已知∠ABC=∠BAD，添加下列条件还不能判定△ABC≌△BAD的是（）

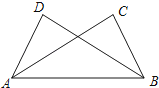A、AC=BD B、∠CAB=∠DBA C、∠C=∠D D、BC=AD

查看试题解析
12. 如图，在△ABC中，∠A=20°，∠ABC与∠ACB的角平分线交于D₁ ， ∠ABD₁与∠ACD₁的角平分线交于点D₂ ，依此类推，∠ABD₄与∠ACD₄的角平分线交于点D₅ ，则∠BD₅C的度数是（　　）

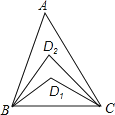A、24° B、25° C、30° D、36°

查看试题解析

二、填空题

13. 若△ABC≌△EFG，且∠B＝60°,∠FGE－∠E＝56°,，则∠A＝度．

查看试题解析
14.
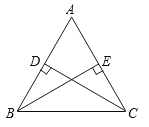
如图，BE，CD是△ABC的高，且BD＝EC，判定△BCD≌△CBE的依据是“”．

查看试题解析
15.
如图，△ABC≌△ADE，∠B＝100°，∠BAC＝30°，那么∠AED＝°．

查看试题解析
16. 如果△ABC和△DEF全等，△DEF和△GHI全等，则△ABC和△GHI全等，如果△ABC和△DEF不全等，△DEF和△GHI全等，则△ABC和△GHI全等．（填“一定”或“不一定”或“一定不”）

查看试题解析
17.
如图，在边长为4的正方形ABCD中，P是BC边上一动点（不含B、C两点），将△ABP沿直线AP翻折，点B落在点E处；在CD上有一点M，使得将△CMP沿直线MP翻折后，点C落在直线PE上的点F处，直线PE交CD于点N，连接MA，NA．则以下结论中正确的有（写出所有正确结论的序号）
①△CMP∽△BPA；
②四边形AMCB的面积最大值为10；
③当P为BC中点时，AE为线段NP的中垂线；
④线段AM的最小值为2 $\sqrt{5}$ ；
⑤当△ABP≌△ADN时，BP=4 $\sqrt{2}$ ﹣4．

查看试题解析

三、综合题

18.
如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．

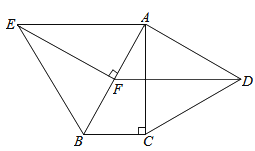(1)、试说明AC=EF；

(2)、求证：四边形ADFE是平行四边形.

查看试题解析
19.
已知：如图，在正方形ABCD中，G是CD上一点，延长BC到E，使CE=CG，连接BG并延长交DE于F．

(1)、求证：△BCG≌△DCE；

(2)、将△DCE绕点D顺时针旋转90°得到△DAE′，判断四边形E′BGD是什么特殊四边形，并说明理由。

查看试题解析
20. 如果将四根木条首尾相连，在相连处用螺钉连接，就能构成一个平面图形．

(1)、若固定三根木条AB，BC，AD不动，AB=AD=2cm，BC=5cm，如图，量得第四根木条CD=5cm，判断此时∠B与∠D是否相等，并说明理由．

(2)、若固定一根木条AB不动，AB=2cm，量得木条CD=5cm，如果木条AD，BC的长度不变，当点D移到BA的延长线上时，点C也在BA的延长线上；当点C移到AB的延长线上时，点A、C、D能构成周长为30cm的三角形，求出木条AD，BC的长度．

查看试题解析
21. 根据直角三角形的判定的知识解决下列问题

(1)、
如图①所示，P是等边△ABC内的一点，连接PA、PB、PC，将△BAP绕B点顺时针旋转60°得△BCQ，连接PQ．若PA2+PB2=PC2，证明∠PQC=90°；

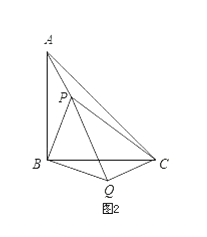
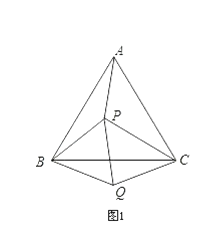(2)、
如图②所示，P是等腰直角△ABC（∠ABC=90°）内的一点，连接PA、PB、PC，将△BAP绕B点顺时针旋转90°得△BCQ，连接PQ．当PA、PB、PC满足什么条件时，∠PQC=90°？请说明．

查看试题解析
22.
如图，在平面直角坐标系中，已知抛物线y=x²+bx+c过A，B，C三点，点A的坐标是（3，0），点C的坐标是（0，﹣3），动点P在抛物线上．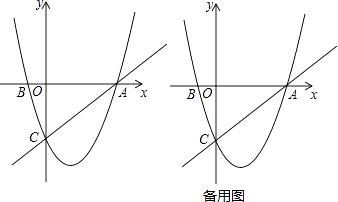

(1)、b= ， c= ，点B的坐标为；（直接填写结果）

(2)、是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；

(3)、过动点P作PE垂直y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标．

查看试题解析
23.
如图，抛物线经过A（﹣1，0），B（5，0），C（0，- $\frac{5}{2}$ ）三点．

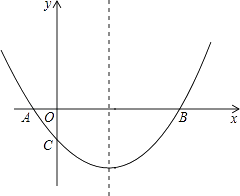(1)、求抛物线的解析式；

(2)、在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；

(3)、点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．

查看试题解析