中考备考专题复习：三角形及其性质

试卷更新日期：2017-02-08 类型：二轮复习

进入出卷网下载

一、单选题

1. 等腰三角形的两边长分别为3、6，则该三角形的周长为（）

A、12或15 B、9 C、12 D、15

查看试题解析
2. 不一定在三角形内部的线段是（）

A、三角形的角平分线 B、三角形的中线 C、三角形的高 D、三角形的中位线

查看试题解析
3. △ABC中，∠A、∠B、∠C的对边分别是a、b、c，下列说法中，错误的是（　　）

A、如果∠C﹣∠B=∠A，那么∠C=90° B、如果∠C=90°，那么c²﹣b²=a² C、如果（a+b）（a﹣b）=c² ，那么∠C=90° D、如果∠A=30°∠B=60°，那么AB=2BC

查看试题解析
4.
如图所示，AD是△ABC的中线，∠ADC＝45°，把△ADC沿AD对折，使点C落在点C´的位置，则图中的一个等腰直角三角形是（）

A、△ADC′ B、△BDC′ C、△ADC D、不存在

查看试题解析
5.
如图，AD⊥BC，GC⊥BC，CF⊥AB，垂足分别是D、C、F，下列说法中，错误的是（　　）

A、△ABC中，AD是边BC上的高 B、△ABC中，GC是边BC上的高 C、△GBC中，GC是边BC上的高 D、△GBC中，CF是边BG上的高

查看试题解析
6. 如图，在△ABC中，已知点E、F分别是AD、CE边上的中点，且S_△_BEF=4cm² ，则S_△_ABC的值为（　　）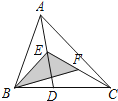

A、1cm² B、2cm² C、8cm² D、16cm²

查看试题解析
7. 下列图形中具有稳定性的有（　　）

A、2个 B、3个 C、4个 D、5个

查看试题解析
8. 工人师傅要将边长为4m和3m的平行四边形框架固定，现有下列长度的木棒，在木棒的两端钉上达到固定平行四边形的目的，不符合要求的是（　　）

A、2m B、3m C、4m D、8m

查看试题解析
9.
如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=50°，则∠CDE的度数为（　　）

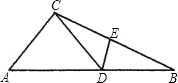A、50° B、51° C、51.5° D、52.5°

查看试题解析
10.
如图，⊙O中，弦AB与CD交于点M，∠A=45°，∠AMD=75°，则∠B的度数是（）

A、15° B、25° C、30° D、75°

查看试题解析
11.
如图所示，用量角器度量∠AOB，可以读出∠AOB的度数为（）

A、45° B、55° C、125° D、135°

查看试题解析
12.
如图1，点E为矩形ABCD边AD上一点，点P，点Q同时从点B出发，点P沿BE→ED→DC 运动到点C停止，点Q沿BC运动到点C停止，它们运动的速度都是1cm/s，设P，Q出发t秒时，△BPQ的面积为ycm² ，已知y与t的函数关系的图形如图2（曲线OM为抛物线的一部分），则下列结论：①AD=BE=5cm；②当0＜t≤5时， $y = \frac{2}{5} t^{2}$ ；③直线NH的解析式为 $y = - \frac{5}{2} t + 27$ ；④若△ABE与△QBP相似，则t= $\frac{29}{4}$ 秒。其中正确的结论个数为( )

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

13. 半径等于12的圆中，垂直平分半径的弦长为．

查看试题解析
14.
在△ABC中，∠B，∠C的平分线交于点O，若∠BOC=132°，则∠A=度.

查看试题解析
15.
已知如图所示，∠MON＝40°，P为∠MON内一点，A为OM上一点，B为ON上一点，则当△PAB的周长取最小值时，∠APB的度数为°．

查看试题解析
16.
如图，观察图中每一个大三角形中白色三角形的排列规律，则第5个大三角形中白色三角形有个．

查看试题解析
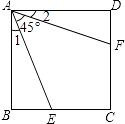
17.
如图，已知正方形ABCD边长为1，∠EAF=45°，AE=AF，则有下列结论：
①∠1=∠2=22.5°；
②点C到EF的距离是 $\sqrt{2}$ -1；
③△ECF的周长为2；
④BE+DF＞EF．
其中正确的结论是．（写出所有正确结论的序号）

查看试题解析

三、解答题

18.
如图，在直角△ABC中，∠C＝90°，∠CAB的平分线AD交BC于D，若DE垂直平分AB，求∠B的度数．

查看试题解析

四、综合题

19.
如图，△ABC中，AB＝AC，∠A＝36°，AC的垂直平分线交AB于E，D为垂足，连接EC．

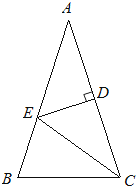(1)、求∠ECD的度数；

(2)、若CE＝5，求BC长．

查看试题解析
20. 已知抛物线C：y=x²﹣2x+1的顶点为P，与y轴的交点为Q，点F（1， $\frac{1}{2}$ ）．

(1)、求点P，Q的坐标；

(2)、将抛物线C向上平移得到抛物线C′，点Q平移后的对应点为Q′，且FQ′=OQ′．
①求抛物线C′的解析式；
②若点P关于直线Q′F的对称点为K，射线FK与抛物线C′相交于点A，求点A的坐标．

查看试题解析
21.
在△ABC中，∠B=45°，∠C=30°，点D是BC上一点，连接AD，过点A作AG⊥AD，在AG上取点F，连接DF．延长DA至E，使AE=AF，连接EG，DG，且GE=DF．

(1)、若AB=2 $\sqrt{2}$ ，求BC的长；

(2)、如图1，当点G在AC上时，求证：BD= $\frac{1}{2}$ CG；

(3)、如图2，当点G在AC的垂直平分线上时，直接写出 $\frac{A B}{C G}$ 的值．

查看试题解析
22. 如果将四根木条首尾相连，在相连处用螺钉连接，就能构成一个平面图形．

(1)、若固定三根木条AB，BC，AD不动，AB=AD=2cm，BC=5cm，如图，量得第四根木条CD=5cm，判断此时∠B与∠D是否相等，并说明理由．

(2)、若固定一根木条AB不动，AB=2cm，量得木条CD=5cm，如果木条AD，BC的长度不变，当点D移到BA的延长线上时，点C也在BA的延长线上；当点C移到AB的延长线上时，点A、C、D能构成周长为30cm的三角形，求出木条AD，BC的长度．

查看试题解析
23.
如图所示，在平面直角坐标系中，过点A（﹣ $\sqrt{3}$ ，0）的两条直线分别交y轴于B、C两点，且B、C两点的纵坐标分别是一元二次方程x²﹣2x﹣3=0的两个根

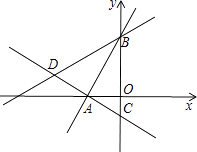(1)、求线段BC的长度；

(2)、试问：直线AC与直线AB是否垂直？请说明理由；

(3)、若点D在直线AC上，且DB=DC，求点D的坐标；

(4)、在（3）的条件下，直线BD上是否存在点P，使以A、B、P三点为顶点的三角形是等腰三角形？若存在，请直接写出P点的坐标；若不存在，请说明理由．

查看试题解析