中考备考专题复习:图形的初步
试卷更新日期:2017-02-08 类型:二轮复习
一、单选题
-
1. 下列说法正确的是( )
A、长方体的截面一定是长方形 B、了解一批日光灯的使用寿命适合采用的调查方式是普查 C、一个圆形和它平移后所得的圆形全等 D、多边形的外角和不一定都等于360°2.如图,以BC为公共边的三角形的个数是( )
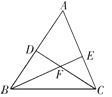 A、2 B、3 C、4 D、53. 下列图形中,属于立体图形的是( )A、
A、2 B、3 C、4 D、53. 下列图形中,属于立体图形的是( )A、 B、
B、 C、
C、 D、
D、 4.
4.足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )
 A、点C B、点D或点E C、线段DE(异于端点) 上一点 D、线段CD(异于端点) 上一点5. 在同一直线上,线段AB=4cm,线段BC=3cm,则线段AC=( )A、7cm B、12cm C、1cm D、7cm或1cm6.
A、点C B、点D或点E C、线段DE(异于端点) 上一点 D、线段CD(异于端点) 上一点5. 在同一直线上,线段AB=4cm,线段BC=3cm,则线段AC=( )A、7cm B、12cm C、1cm D、7cm或1cm6.如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )
 A、75°36′ B、75°12′ C、74°36′ D、74°12′7. 轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.
A、75°36′ B、75°12′ C、74°36′ D、74°12′7. 轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.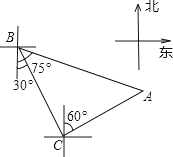 A、25 B、25 C、50 D、258. 如图是一个正方体,则它的表面展开图可以是( )
A、25 B、25 C、50 D、258. 如图是一个正方体,则它的表面展开图可以是( )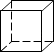 A、
A、 B、
B、 C、
C、 D、
D、 9.
9.如图,在方格纸中有四个图形<1>、<2>、<3>、<4>,其中面积相等的图形是 ( )
 A、<2>和<3> B、<1>和<2> C、<2>和<4> D、<1>和<4>10. 平面内的9条直线任两条都相交,交点数最多有m个,最少有n个,则m+n等于( )A、36 B、37 C、38 D、3911. 如图(一),
A、<2>和<3> B、<1>和<2> C、<2>和<4> D、<1>和<4>10. 平面内的9条直线任两条都相交,交点数最多有m个,最少有n个,则m+n等于( )A、36 B、37 C、38 D、3911. 如图(一), 为一条拉直的细线,A、B两点在
为一条拉直的细线,A、B两点在  上,且 : =1:3,
上,且 : =1:3,  :
:  =3:5.若先固定B点,将
=3:5.若先固定B点,将  折向
折向  ,使得
,使得  重叠在
重叠在  上,如图(二),再从图(二) 的A点及与A点重叠处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为何?( )
上,如图(二),再从图(二) 的A点及与A点重叠处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为何?( ) 
A、1:1:1 B、1:1:2 C、1:2:2 D、1:2:512. 如图,已知A,B是线段EF上两点,EA:AB:BF=1:2:3,M,N分别为EA,BF的中点,且MN=8cm,则EF长( ) A、9cm B、10cm C、11cm D、12cm13.
A、9cm B、10cm C、11cm D、12cm13.将如图绕AB边旋转一周,所得几何体的俯视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、 14. 如图是一个正方体,则它的表面展开图可以是( )
14. 如图是一个正方体,则它的表面展开图可以是( )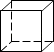 A、
A、 B、
B、 C、
C、 D、
D、 15. 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
15. 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( ) A、垂线段最短 B、经过一点有无数条直线 C、经过两点,有且仅有一条直线 D、两点之间,线段最短
A、垂线段最短 B、经过一点有无数条直线 C、经过两点,有且仅有一条直线 D、两点之间,线段最短二、填空题
-
16. 如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 .
17. 如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为 . 18. 如图所示,1条直线将平面分成2个部分,2条直线最多可将平面分成4个部分,3条直线最多可将平面分成7个部分,4条直线最多可将平面分成11个部分.现有n条直线最多可将平面分成56个部分,则n的值为 .
18. 如图所示,1条直线将平面分成2个部分,2条直线最多可将平面分成4个部分,3条直线最多可将平面分成7个部分,4条直线最多可将平面分成11个部分.现有n条直线最多可将平面分成56个部分,则n的值为 . 19. 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是cm.
19. 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是cm. 20.
20.我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
图形的变化
示例图形
与对应线段有关的结论
与对应点有关的结论
平移

AA′=BB′
AA′∥BB′
轴对称

旋转

AB=A′B′;对应线段AB和A′B′所在的直线相交所成的角与旋转角相等或互补.
三、解答题
-
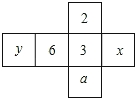
21. 如图是一个正方体的展开图,标注了字母a的面是正方体的正面,如果正方体相对两个面上的整式的值相等,求整式(x+y)a的值.
 22. 如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
22. 如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.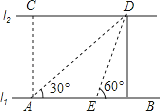
四、综合题
-
23.
从棱长为2的正方体毛坯的一角挖去一个棱长为1的小正方体,得到一个如图的零件,求:
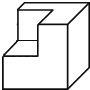 (1)、这个零件的表面积(包括底面);
(1)、这个零件的表面积(包括底面);
(2)、这个零件的体积.
24.有一种牛奶软包装盒如图1所示.为了生产这种包装盒,需要先画出展开图纸样.
 (1)、如图2给出三种纸样甲.乙.丙,在甲.乙.丙中,正确的有 .(2)、从已知正确的纸样中选出一种,在原图上标注上尺寸.(3)、利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和)25. 在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.
(1)、如图2给出三种纸样甲.乙.丙,在甲.乙.丙中,正确的有 .(2)、从已知正确的纸样中选出一种,在原图上标注上尺寸.(3)、利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和)25. 在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.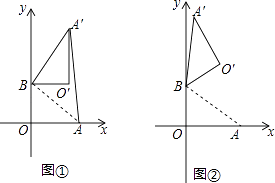 (1)、如图①,若α=90°,求AA′的长;(2)、如图②,若α=120°,求点O′的坐标;(3)、在(2)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可)26.
(1)、如图①,若α=90°,求AA′的长;(2)、如图②,若α=120°,求点O′的坐标;(3)、在(2)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可)26.观察下图,思考问题:
 (1)、你认识上面的图片中的哪些物体?(2)、这些物体的表面形状类似与哪些几何体?说说你的理由。(3)、你能再举出一些常见的图形吗?27. 回答下列问题:(1)、
(1)、你认识上面的图片中的哪些物体?(2)、这些物体的表面形状类似与哪些几何体?说说你的理由。(3)、你能再举出一些常见的图形吗?27. 回答下列问题:(1)、如图所示的甲、乙两个平面图形能折什么几何体?
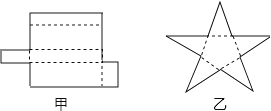 (2)、由多个平面围成的几何体叫做多面体.若一个多面体的面数为f , 顶点个数为v , 棱数为e , 分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?(3)、应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.28. 如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M、N分别是AC、BC的中点.
(2)、由多个平面围成的几何体叫做多面体.若一个多面体的面数为f , 顶点个数为v , 棱数为e , 分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?(3)、应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.28. 如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M、N分别是AC、BC的中点. (1)、求线段MN的长;(2)、若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;(3)、若C在线段AB的延长线上,且满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由;(4)、你能用一句简洁的话,描述你发现的结论吗?
(1)、求线段MN的长;(2)、若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;(3)、若C在线段AB的延长线上,且满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由;(4)、你能用一句简洁的话,描述你发现的结论吗?