中考备考专题复习:二次函数的应用
试卷更新日期:2017-02-07 类型:二轮复习
一、单选题
-
1. 已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为( )A、1或﹣5 B、﹣1或5 C、1或﹣3 D、1或32. 在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点旋转180°得到抛物线y=x2+5x+6,则原抛物线的解析式是( )
A、y=﹣(x﹣ )2﹣ B、y=﹣(x+ )2﹣ C、y=﹣(x﹣ )2﹣ D、y=﹣(x+ )2+3. 已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )A、当a=1时,函数图象过点(﹣1,1) B、当a=﹣2时,函数图象与x轴没有交点 C、若a>0,则当x≥1时,y随x的增大而减小 D、若a<0,则当x≤1时,y随x的增大而增大4. 以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A、b≥ B、b≥1或b≤﹣1 C、b≥2 D、1≤b≤25. 某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出20件.设每件商品降价x元后,每星期售出商品的总销售额为y元,则y与x的关系式为( )A、y=60(300+20x) B、y=(60﹣x)(300+20x) C、y=300(60﹣20x) D、y=(60﹣x)(300﹣20x)6.如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:
①abc>0
②4a+2b+c>0
③4ac﹣b2<8a
④ <a<
⑤b>c.
其中含所有正确结论的选项是( )
 A、①③ B、①③④ C、②④⑤ D、①③④⑤7. 若抛物线y=x2﹣2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,则原抛物线图象的解析式应变为( )
A、①③ B、①③④ C、②④⑤ D、①③④⑤7. 若抛物线y=x2﹣2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,则原抛物线图象的解析式应变为( )
A、y=(x﹣2)2+3 B、y=(x﹣2)2+5 C、y=x2﹣1 D、y=x2+48. 在同一平面直角坐标系中,函数y=ax+b与y=ax2﹣bx的图象可能是( )A、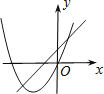 B、
B、 C、
C、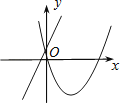 D、
D、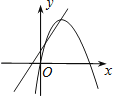 9.
9.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②c>0;③a+c<b;④b2﹣4ac>0,其中正确的个数是( )
 A、1 B、2 C、3 D、410. 已知a≥2,m2﹣2am+2=0,n2﹣2an+2=0,其中 , 则(m﹣1)2+(n﹣1)2的最小值是( )A、6 B、3 C、﹣3 D、011.
A、1 B、2 C、3 D、410. 已知a≥2,m2﹣2am+2=0,n2﹣2an+2=0,其中 , 则(m﹣1)2+(n﹣1)2的最小值是( )A、6 B、3 C、﹣3 D、011.如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )
 A、2a﹣b=0 B、a+b+c>0 C、3a﹣c=0 D、当a= 时,△ABD是等腰直角三角形12. 某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )
A、2a﹣b=0 B、a+b+c>0 C、3a﹣c=0 D、当a= 时,△ABD是等腰直角三角形12. 某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )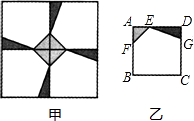 A、
A、 B、
B、 C、
C、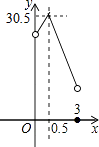 D、
D、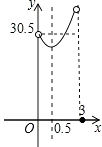
二、填空题
-
13. 已知A(0,3),B(2,3)是抛物线y=﹣x2+bx+c上两点,该抛物线的顶点坐标是 .
14. 某公司今年4月份营业额为60万元,6月份营业额达到100万元,设该公司5、6两个月营业额的月均增长率为x,则可列方程为 .15. 直线y=kx+b与抛物线y= x2交于A(x1 , y1)、B(x2 , y2)两点,当OA⊥OB时,直线AB恒过一个定点,该定点坐标为 .16.二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b﹣2c|,Q=|2a﹣b|﹣|3b+2c|,则P,Q的大小关系是 .
 17. 已知关于x的二次函数y=ax2+bx+c的图象经过点(﹣2,y1),(﹣1,y2),(1,0),且y1<0<y2 , 对于以下结论:
17. 已知关于x的二次函数y=ax2+bx+c的图象经过点(﹣2,y1),(﹣1,y2),(1,0),且y1<0<y2 , 对于以下结论:①abc>0;②a+3b+2c≤0;③对于自变量x的任意一个取值,都有 x2+x≥﹣ ;④在﹣2<x<﹣1中存在一个实数x0 , 使得x0=﹣ ,
其中结论错误的是 (只填写序号).
三、综合题
-
18.
如图,在平面直角坐标系中,二次函数y=﹣ x2+bx+c的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
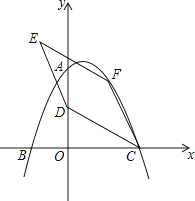 (1)、求该二次函数的表达式及点C的坐标;(2)、点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
(1)、求该二次函数的表达式及点C的坐标;(2)、点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值.
19.课本中有一个例题:
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2 .
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:
 (1)、若AB为1m,求此时窗户的透光面积?(2)、与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.20.
(1)、若AB为1m,求此时窗户的透光面积?(2)、与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.20.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx经过两点A(﹣1,1),B(2,2).过点B作BC∥x轴,交抛物线于点C,交y轴于点D.
 (1)、求此抛物线对应的函数表达式及点C的坐标;(2)、若抛物线上存在点M,使得△BCM的面积为 ,求出点M的坐标;(3)、连接OA、OB、OC、AC,在坐标平面内,求使得△AOC与△OBN相似(边OA与边OB对应)的点N的坐标.21.
(1)、求此抛物线对应的函数表达式及点C的坐标;(2)、若抛物线上存在点M,使得△BCM的面积为 ,求出点M的坐标;(3)、连接OA、OB、OC、AC,在坐标平面内,求使得△AOC与△OBN相似(边OA与边OB对应)的点N的坐标.21.如图1,二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1.
 (1)、求这个二次函数的表达式;(2)、点P在该二次函数的图象上,点Q在x轴上,若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;(3)、如图3,一次函数y=kx(k>0)的图象与该二次函数的图象交于O、C两点,点T为该二次函数图象上位于直线OC下方的动点,过点T作直线TM⊥OC,垂足为点M,且M在线段OC上(不与O、C重合),过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中, 为常数,试确定k的值.22.
(1)、求这个二次函数的表达式;(2)、点P在该二次函数的图象上,点Q在x轴上,若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;(3)、如图3,一次函数y=kx(k>0)的图象与该二次函数的图象交于O、C两点,点T为该二次函数图象上位于直线OC下方的动点,过点T作直线TM⊥OC,垂足为点M,且M在线段OC上(不与O、C重合),过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中, 为常数,试确定k的值.22.如图1,在平面直角坐标系中,抛物线y=﹣ x2+ x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E.
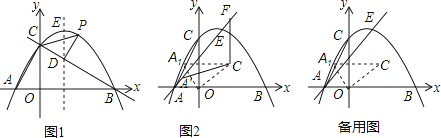 (1)、判断△ABC的形状,并说明理由;(2)、经过B,C两点的直线交抛物线的对称轴于点D,点P为直线BC上方抛物线上的一动点,当△PCD的面积最大时,Q从点P出发,先沿适当的路径运动到抛物线的对称轴上点M处,再沿垂直于抛物线对称轴的方向运动到y轴上的点N处,最后沿适当的路径运动到点A处停止.当点Q的运动路径最短时,求点N的坐标及点Q经过的最短路径的长;(3)、如图2,平移抛物线,使抛物线的顶点E在射线AE上移动,点E平移后的对应点为点E′,点A的对应点为点A′,将△AOC绕点O顺时针旋转至△A1OC1的位置,点A,C的对应点分别为点A1 , C1 , 且点A1恰好落在AC上,连接C1A′,C1E′,△A′C1E′是否能为等腰三角形?若能,请求出所有符合条件的点E′的坐标;若不能,请说明理由.
(1)、判断△ABC的形状,并说明理由;(2)、经过B,C两点的直线交抛物线的对称轴于点D,点P为直线BC上方抛物线上的一动点,当△PCD的面积最大时,Q从点P出发,先沿适当的路径运动到抛物线的对称轴上点M处,再沿垂直于抛物线对称轴的方向运动到y轴上的点N处,最后沿适当的路径运动到点A处停止.当点Q的运动路径最短时,求点N的坐标及点Q经过的最短路径的长;(3)、如图2,平移抛物线,使抛物线的顶点E在射线AE上移动,点E平移后的对应点为点E′,点A的对应点为点A′,将△AOC绕点O顺时针旋转至△A1OC1的位置,点A,C的对应点分别为点A1 , C1 , 且点A1恰好落在AC上,连接C1A′,C1E′,△A′C1E′是否能为等腰三角形?若能,请求出所有符合条件的点E′的坐标;若不能,请说明理由.