中考备考专题复习:二次函数
试卷更新日期:2017-02-07 类型:二轮复习
一、单选题
-
1. 已知二次函数y=x2+x+c的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是( )A、(1,0) B、(-1,0) C、(2,0) D、(-2,0)2.
如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
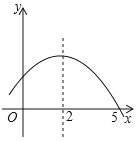 A、-1<x<5 B、x>5 C、x<-1且x>5 D、x<-1或x>53. 下列函数中,满足y的值随x的值增大而增大的是( )A、y=﹣2x B、y=3x﹣1 C、y= D、y=x24. 已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )A、当a=1时,函数图象过点(﹣1,1) B、当a=﹣2时,函数图象与x轴没有交点 C、若a>0,则当x≥1时,y随x的增大而减小 D、若a<0,则当x≤1时,y随x的增大而增大5. 在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点旋转180°得到抛物线y=x2+5x+6,则原抛物线的解析式是( )
A、-1<x<5 B、x>5 C、x<-1且x>5 D、x<-1或x>53. 下列函数中,满足y的值随x的值增大而增大的是( )A、y=﹣2x B、y=3x﹣1 C、y= D、y=x24. 已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )A、当a=1时,函数图象过点(﹣1,1) B、当a=﹣2时,函数图象与x轴没有交点 C、若a>0,则当x≥1时,y随x的增大而减小 D、若a<0,则当x≤1时,y随x的增大而增大5. 在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点旋转180°得到抛物线y=x2+5x+6,则原抛物线的解析式是( )
A、y=﹣(x﹣ )2﹣ B、y=﹣(x+ )2﹣ C、y=﹣(x﹣ )2﹣ D、y=﹣(x+ )2+6. 以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A、b≥ B、b≥1或b≤﹣1 C、b≥2 D、1≤b≤27. 二次函数y=x2﹣2x+4化为y=a(x﹣h)2+k的形式,下列正确的是( )A、y=(x﹣1)2+2 B、y=(x﹣1)2+3 C、y=(x﹣2)2+2 D、y=(x﹣2)2+48. 一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A、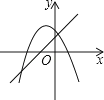 B、
B、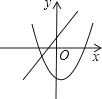 C、
C、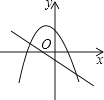 D、
D、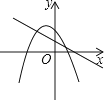 9. 已知a≥2,m2﹣2am+2=0,n2﹣2an+2=0,其中 , 则(m﹣1)2+(n﹣1)2的最小值是( )A、6 B、3 C、﹣3 D、010. 抛物线y=x2+bx+c(其中b,c是常数)过点A(2,6),且抛物线的对称轴与线段y=0(1≤x≤3)有交点,则c的值不可能是( )A、4 B、6 C、8 D、1011. 一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
9. 已知a≥2,m2﹣2am+2=0,n2﹣2an+2=0,其中 , 则(m﹣1)2+(n﹣1)2的最小值是( )A、6 B、3 C、﹣3 D、010. 抛物线y=x2+bx+c(其中b,c是常数)过点A(2,6),且抛物线的对称轴与线段y=0(1≤x≤3)有交点,则c的值不可能是( )A、4 B、6 C、8 D、1011. 一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( ) A、
A、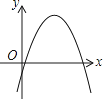 B、
B、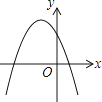 C、
C、 D、
D、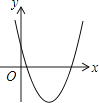 12. 某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )
12. 某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )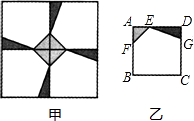 A、
A、 B、
B、 C、
C、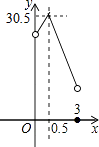 D、
D、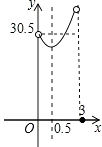
二、填空题
-
13. 如果函数是关于x的二次函数, 则k= 。14. 已知A(0,3),B(2,3)是抛物线y=﹣x2+bx+c上两点,该抛物线的顶点坐标是 .
15. 直线y=kx+b与抛物线y= x2交于A(x1 , y1)、B(x2 , y2)两点,当OA⊥OB时,直线AB恒过一个定点,该定点坐标为 .16. 已知关于x的二次函数y=ax2+bx+c的图象经过点(﹣2,y1),(﹣1,y2),(1,0),且y1<0<y2 , 对于以下结论:①abc>0;②a+3b+2c≤0;③对于自变量x的任意一个取值,都有 x2+x≥﹣ ;④在﹣2<x<﹣1中存在一个实数x0 , 使得x0=﹣ ,
其中结论错误的是 (只填写序号).
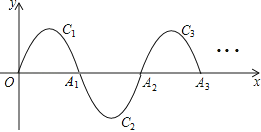
17.如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1 , 它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2 , 交x轴于A2;将C2绕A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C6 , 若点P(11,m)在第6段抛物线C6上,则m= .
三、综合题
-
18. 在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题:
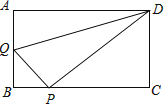 (1)、设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值;(2)、是否存在x的值,使得QP⊥DP?试说明理由.19. 在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.
(1)、设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值;(2)、是否存在x的值,使得QP⊥DP?试说明理由.19. 在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.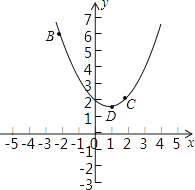 (1)、试求抛物线的解析式;(2)、记抛物线顶点为D,求△BCD的面积;(3)、若直线y=﹣ x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.20. 正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.
(1)、试求抛物线的解析式;(2)、记抛物线顶点为D,求△BCD的面积;(3)、若直线y=﹣ x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.20. 正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点. (1)、建立适当的平面直角坐标系,
(1)、建立适当的平面直角坐标系,①直接写出O、P、A三点坐标;
②求抛物线L的解析式;
(2)、求△OAE与△OCE面积之和的最大值.
21. 如图,抛物线y=x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3).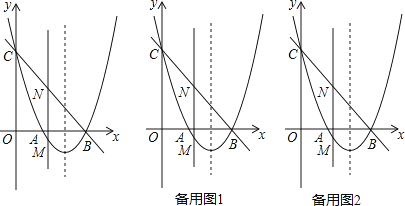 (1)、求抛物线的解析式;(2)、若点M是抛物线在x轴下方上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值;(3)、在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.22. 如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.
(1)、求抛物线的解析式;(2)、若点M是抛物线在x轴下方上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值;(3)、在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.22. 如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.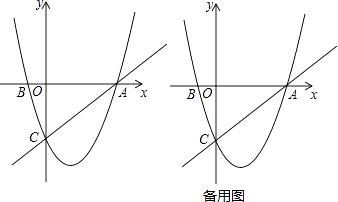 (1)、b= , c= , 点B的坐标为;(直接填写结果)(2)、是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)、过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.23. 如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC.
(1)、b= , c= , 点B的坐标为;(直接填写结果)(2)、是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)、过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.23. 如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC. (1)、求该抛物线的解析式,并用配方法把解析式化为y=a(x﹣h)2+k的形式;(2)、若点H(1,y)在BC上,连接FH,求△FHB的面积;(3)、一动点M从点D出发,以每秒1个单位的速度平沿行与y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?(4)、在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(1)、求该抛物线的解析式,并用配方法把解析式化为y=a(x﹣h)2+k的形式;(2)、若点H(1,y)在BC上,连接FH,求△FHB的面积;(3)、一动点M从点D出发,以每秒1个单位的速度平沿行与y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?(4)、在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请直接写出点P的坐标;若不存在,请说明理由.