中考备考专题复习:反比例函数
试卷更新日期:2017-02-07 类型:二轮复习
一、单选题
-
1. 已知反比例函数y= ,当1<x<3时,y的最小整数值是( )A、3 B、4 C、5 D、62. 如果等腰三角形的底边长为x,底边上的高为y,则它的面积为定植S时,则x与y的函数关系式为( )A、y= B、y= C、y= D、y=3. 已知A(x1 , y1)、B(x2 , y2)、C(x3 , y3)是反比例函数y= 上的三点,若x1<x2<x3 , y2<y1<y3 , 则下列关系式不正确的是( )A、x1•x2<0 B、x1•x3<0 C、x2•x3<0 D、x1+x2<04. 将一次函数y=x图象向下平移b个单位,与双曲线y=交于点A,与x轴交于点B,则OA2-OB2=( )A、-2 B、2 C、- D、5.
如图所示,点P(3a,a)是反比例函数y=(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
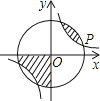 A、y= B、y= C、y= D、y=6.
A、y= B、y= C、y= D、y=6.如图,△AOB为等边三角形,点A在第四象限,点B的坐标为(4,0),过点C(
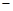 4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数y=(k≠0)图象上,当△ADE和△DCO的面积相等时,k的值为( )
4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数y=(k≠0)图象上,当△ADE和△DCO的面积相等时,k的值为( ) A、- B、- C、-3 D、-67.
A、- B、- C、-3 D、-67.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
 A、7:20 B、7:30 C、7:45 D、7:508.
A、7:20 B、7:30 C、7:45 D、7:508.如图,反比例函数y=的图象经过二次函数y=ax2+bx图象的顶点(﹣ , m)(m>0),则有( )
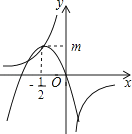 A、a=b+2k B、a=b﹣2k C、k<b<0 D、a<k<09.
A、a=b+2k B、a=b﹣2k C、k<b<0 D、a<k<09.如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=﹣(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
 A、 B、 C、 D、10.
A、 B、 C、 D、10.如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ,反比例函数y= 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
 A、60 B、80 C、30 D、4011.
A、60 B、80 C、30 D、4011.一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
 A、
A、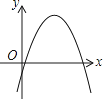 B、
B、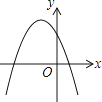 C、
C、 D、
D、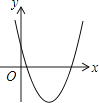 12. 若点A(﹣5,y1),B(﹣3,y2),C(2,y3)在反比例函数y= 的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y3<y2 B、y1<y2<y3 C、y3<y2<y1 D、y2<y1<y3
12. 若点A(﹣5,y1),B(﹣3,y2),C(2,y3)在反比例函数y= 的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y3<y2 B、y1<y2<y3 C、y3<y2<y1 D、y2<y1<y3二、填空题
-
13. 如果函数y=x2m-1为反比例函数,则m的值是.14. 反比例函数y=的图象有一支位于第一象限,则常数a的取值范围是 .15.
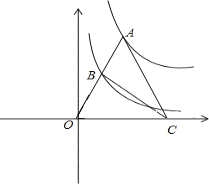
如图,点A为函数y= (x>0)图象上一点,连结OA,交函数y= (x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 .
 16.
16.如图,一次函数y=﹣x+b与反比例函数y= (x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.
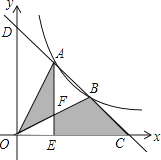 (1)、b=(用含m的代数式表示);(2)、若S△OAF+S四边形EFBC=4,则m的值是 .17. 如图,已知直线l:y=﹣x,双曲线y= ,在l上取一点A(a,﹣a)(a>0),过A作x轴的垂线交双曲线于点B,过B作y轴的垂线交l于点C,过C作x轴的垂线交双曲线于点D,过D作y轴的垂线交l于点E,此时E与A重合,并得到一个正方形ABCD,若原点O在正方形ABCD的对角线上且分这条对角线为1:2的两条线段,则a的值为 .
(1)、b=(用含m的代数式表示);(2)、若S△OAF+S四边形EFBC=4,则m的值是 .17. 如图,已知直线l:y=﹣x,双曲线y= ,在l上取一点A(a,﹣a)(a>0),过A作x轴的垂线交双曲线于点B,过B作y轴的垂线交l于点C,过C作x轴的垂线交双曲线于点D,过D作y轴的垂线交l于点E,此时E与A重合,并得到一个正方形ABCD,若原点O在正方形ABCD的对角线上且分这条对角线为1:2的两条线段,则a的值为 .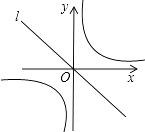
三、解答题
-
18. 当m取何值时,函数是反比例函数?19.
如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y= (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
 20.
20.已知与是反比例函数图象上的两个点.
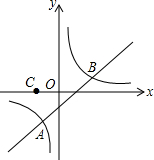
(1)求m和k的值
(2)若点C(-1,0),连结AC,BC,求△ABC的面积
(3)根据图象直接写出一次函数的值大于反比例函数的值的的取值范围.四、综合题
-
21. 在平面直角坐标系中,把横纵坐标都是整数的点称为“整点”.
 (1)、直接写出函数y= 图象上的所有“整点”A1 , A2 , A3 , …的坐标;(2)、在(1)的所有整点中任取两点,用树状图或列表法求出这两点关于原点对称的概率.22.
(1)、直接写出函数y= 图象上的所有“整点”A1 , A2 , A3 , …的坐标;(2)、在(1)的所有整点中任取两点,用树状图或列表法求出这两点关于原点对称的概率.22.已知反比例函数y=的图象的一支位于第一象限.
 (1)、判断该函数图象的另一支所在的象限,并求m的取值范围;(2)、
(1)、判断该函数图象的另一支所在的象限,并求m的取值范围;(2)、如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.
 23.
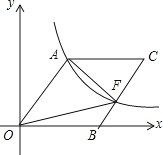
23.如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y= (k>0)的图象与BC边交于点E.
 (1)、当F为AB的中点时,求该函数的解析式;(2)、当k为何值时,△EFA的面积最大,最大面积是多少?24.
(1)、当F为AB的中点时,求该函数的解析式;(2)、当k为何值时,△EFA的面积最大,最大面积是多少?24.已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,且与双曲线y= 交于点C(1,a).
 (1)、试确定双曲线的函数表达式;(2)、将l1沿y轴翻折后,得到l2 , 画出l2的图象,并求出l2的函数表达式;(3)、在(2)的条件下,点P是线段AC上点(不包括端点),过点P作x轴的平行线,分别交l2于点M,交双曲线于点N,求S△AMN的取值范围.
(1)、试确定双曲线的函数表达式;(2)、将l1沿y轴翻折后,得到l2 , 画出l2的图象,并求出l2的函数表达式;(3)、在(2)的条件下,点P是线段AC上点(不包括端点),过点P作x轴的平行线,分别交l2于点M,交双曲线于点N,求S△AMN的取值范围.