中考备考专题复习:一次函数及其运用
试卷更新日期:2017-02-07 类型:二轮复习
一、单选题
-
1. 若(2,k)是双曲线y=上的一点,则函数y=(k-1)x的图象经过( )A、第一、三象限 B、第二、四象限 C、第一、二象限 D、第三、四象限2. 次函数y=mx+|m-1|的图象过点(0,2),且y随x的增大而增大,则m=( )A、-1 B、3 C、1 D、-1或33. 若函数y=(a-5)x1-b+b是一次函数,则a、b应满足的条件是( ).A、a=5且b≠0 B、a=5且b=0 C、a≠5且b≠0 D、a≠5且b=04. 下列函数中,满足y的值随x的值增大而增大的是( )A、y=﹣2x B、y=3x﹣1 C、y= D、y=x25.
一次函数的图象如图所示,当-3<y<3时的取值范围是( )
 A、x>4 B、0<x<2 C、0<x<4 D、2<x<46.
A、x>4 B、0<x<2 C、0<x<4 D、2<x<46.如图,一次函数图象经过点A,且与正比例函数y=-x的图象交于点B,则该一次函数的表达式为( )
 A、y=-x+2 B、y=x+2 C、y=x-2 D、y=-x-27. 如图,直线y=ax+b过点A(0,2)和点B(﹣3,0),则方程ax+b=0的解是( )
A、y=-x+2 B、y=x+2 C、y=x-2 D、y=-x-27. 如图,直线y=ax+b过点A(0,2)和点B(﹣3,0),则方程ax+b=0的解是( )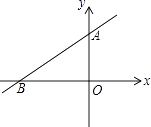 A、x=2 B、x=0 C、x=﹣1 D、x=﹣38. 二次函数y=ax2+bx+c(a,b,c为常数且a≠0)的图象如图所示,则一次函数y=ax+b与反比例函数y= 的图象可能是( )
A、x=2 B、x=0 C、x=﹣1 D、x=﹣38. 二次函数y=ax2+bx+c(a,b,c为常数且a≠0)的图象如图所示,则一次函数y=ax+b与反比例函数y= 的图象可能是( )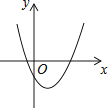 A、
A、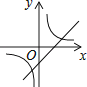 B、
B、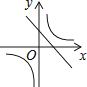 C、
C、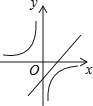 D、
D、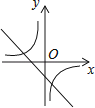 9. 一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
9. 一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( ) A、
A、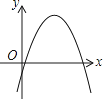 B、
B、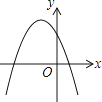 C、
C、 D、
D、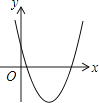 10. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )
10. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )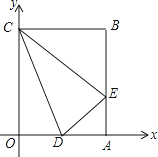 A、(3,1) B、(3, ) C、(3, ) D、(3,2)11. 如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A、(3,1) B、(3, ) C、(3, ) D、(3,2)11. 如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )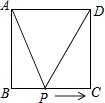 A、
A、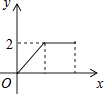 B、
B、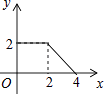 C、
C、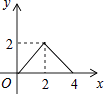 D、
D、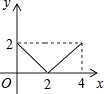 12.
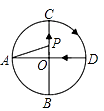
12.如图,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动,设∠APB=y(单位:度),点P运动的时间为x(单位:秒),那么表示y与x关系的图象是( )
 A、
A、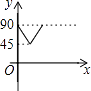 B、
B、 C、
C、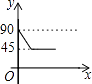 D、
D、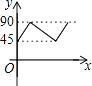
二、填空题
-
13. 已知关于x的方程mx+3=4的解为x=1,则直线y=(m﹣2)x﹣3一定不经过第象限.14. 若一次函数y=﹣2x+b(b为常数)的图象经过第二、三、四象限,则b的值可以是(写出一个即可).15. 如图,有四张不透明的卡片除正面的函数关系式不同外,其余相同,将它们背面朝上洗匀后,从中抽取一张卡片,则抽到函数图象不经过第四象限的卡片的概率为 .
 16. 如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 .
16. 如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 . 17. 如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y= x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y= x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是( ,1),则点A8的横坐标是 .
17. 如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y= x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y= x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是( ,1),则点A8的横坐标是 .
三、解答题
-
18. 如图,直线x-2y=-5和x+y=1分别与x轴交于A、B两点,这两条线的交点为P.
(1)求点P的坐标.
(2)求△APB的面积. 19. 已知一次函数y=(m﹣2)x﹣3m2+12,问:
19. 已知一次函数y=(m﹣2)x﹣3m2+12,问:(1)m为何值时,函数图象过原点?
(2)m为何值时,函数图象平行于直线y=2x?
(3)m为何值时,函数图象过点(0,﹣15),且y随x的增大而减小?
四、综合题
-
20. 某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过200度时,按0.55元/度计费;月用电量超过200度时,其中的200度仍按0.55元/度计费,超过部分按0.70元/度计费.设每户家庭月用电量为x度时,应交电费y元.(1)、分别求出0≤x≤200和x>200时,y与x的函数表达式;(2)、小明家5月份交纳电费117元,小明家这个月用电多少度?21. 根据卫生防疫部门要求,游泳池必须定期换水,清洗.某游泳池周五早上8:00打开排水孔开始排水,排水孔的排水速度保持不变,期间因清洗游泳池需要暂停排水,游泳池的水在11:30全部排完.游泳池内的水量Q(m2)和开始排水后的时间t(h)之间的函数图象如图所示,根据图象解答下列问题:
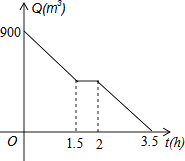 (1)、暂停排水需要多少时间?排水孔排水速度是多少?(2)、当2≤t≤3.5时,求Q关于t的函数表达式.22. 对于坐标平面内的点,现将该点向右平移1个单位,再向上平移2的单位,这种点的运动称为点A的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5),已知点A的坐标为(1,0).
(1)、暂停排水需要多少时间?排水孔排水速度是多少?(2)、当2≤t≤3.5时,求Q关于t的函数表达式.22. 对于坐标平面内的点,现将该点向右平移1个单位,再向上平移2的单位,这种点的运动称为点A的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5),已知点A的坐标为(1,0).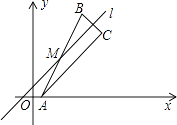 (1)、分别写出点A经1次,2次斜平移后得到的点的坐标.(2)、如图,点M是直线l上的一点,点A关于点M的对称点的点B,点B关于直线l的对称轴为点C.
(1)、分别写出点A经1次,2次斜平移后得到的点的坐标.(2)、如图,点M是直线l上的一点,点A关于点M的对称点的点B,点B关于直线l的对称轴为点C.①若A、B、C三点不在同一条直线上,判断△ABC是否是直角三角形?请说明理由.
②若点B由点A经n次斜平移后得到,且点C的坐标为(7,6),求出点B的坐标及n的值.
23. 随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位不断增加.(1)、该市的养老床位数从2013年底的2万个增长到2015年底的2.88万个,求该市这两年(从2013年度到2015年底)拥有的养老床位数的平均年增长率;(2)、若该市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间(1个养老床位),双人间(2个养老床位),三人间(3个养老床位),因实际需要,单人间房间数在10至30之间(包括10和30),且双人间的房间数是单人间的2倍,设规划建造单人间的房间数为t.①若该养老中心建成后可提供养老床位200个,求t的值;
②求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?24. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B. (1)、若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)、在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)、设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
(1)、若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)、在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)、设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.