中考备考专题复习:点的坐标、函数及其概念
试卷更新日期:2017-02-07 类型:二轮复习
一、单选题
-
1. 在平面直角坐标系中,点(1,5)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 已知点M(1﹣2m,m﹣1)在第四象限,则m的取值范围在数轴上表示正确的是( )
A、 B、
B、 C、
C、 D、
D、 3. 平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )A、5 B、6 C、7 D、84. 园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m)2与工作时间t(h)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( )
3. 平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )A、5 B、6 C、7 D、84. 园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m)2与工作时间t(h)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( ) A、100m2 B、50m2 C、80m2 D、40m25.
A、100m2 B、50m2 C、80m2 D、40m25.如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是( )
 A、(2,﹣3) B、(2,3) C、(3,2) D、(3,﹣2)6.
A、(2,﹣3) B、(2,3) C、(3,2) D、(3,﹣2)6.如图为A、B、C三点在坐标平面上的位置图.若A、B、C的x坐标的数字总和为a,y坐标的数字总和为b,则a﹣b之值为何?( )
 A、5 B、3 C、﹣3 D、﹣57.
A、5 B、3 C、﹣3 D、﹣57.矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )
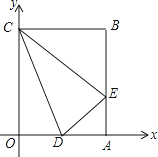 A、(3,1) B、(3, ) C、(3, ) D、(3,2)8.
A、(3,1) B、(3, ) C、(3, ) D、(3,2)8.如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( )
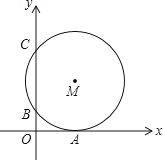 A、10 B、8 C、4 D、29.
A、10 B、8 C、4 D、29.在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
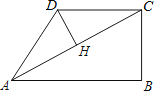 A、
A、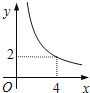 B、
B、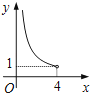 C、
C、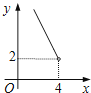 D、
D、 10.
10.如图反映的过程是:小强从家去菜地浇水,又去玉米地除草,然后回家.如果菜地和玉米地的距离为a千米,小强在玉米地除草比在菜地浇水多用的时间为b分钟,则a,b的值分别为( )
 A、1.1,8 B、0.9,3 C、1.1,12 D、0.9,811.
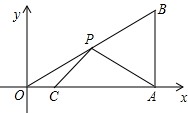
A、1.1,8 B、0.9,3 C、1.1,12 D、0.9,811.如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,),点C的坐标为( , 0),点P为斜边OB上的一动点,则PA+PC的最小值为( ).
 A、 B、 C、 D、212.
A、 B、 C、 D、212.如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3 , …组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2015秒时,点P的坐标是( )
 A、(2014,0) B、(2015,﹣1) C、(2015,1) D、(2016,0)13.
A、(2014,0) B、(2015,﹣1) C、(2015,1) D、(2016,0)13.2013年8月16日,广东省遭受台风“尤特”袭击,大部分地区发生强降雨,某河受暴雨袭击,一天的水位记录如表,观察表中数据,水位上升最快的时段是( )
 A、8~12时 B、12~16时 C、16~20时 D、20~24时14. 已知点A(﹣1,m),B(1,m),C(2,m+1)在同一个函数图象上,这个函数图象可以是( )A、
A、8~12时 B、12~16时 C、16~20时 D、20~24时14. 已知点A(﹣1,m),B(1,m),C(2,m+1)在同一个函数图象上,这个函数图象可以是( )A、 B、
B、 C、
C、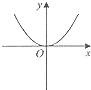 D、
D、 15. 一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )A、
15. 一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
16. 函数y= 的自变量x的取值范围是17. 在平面直角坐标系中,已知线段AB∥x轴,端点A的坐标是(﹣1,4)且AB=4,则端点B的坐标是 .18.
如图是汽车加油站在加油过程中,加油器仪表某一瞬间的显示,请你结合图片信息,解答下列问题:
(1)加油过程中的常量是 ,变量是 ;
(2)请用合适的方式表示加油过程中变量之间的关系
 19.
19.观察图,回答问题:

(1)设图形的周长为L,梯形的个数为n,试写出L与n的函数关系式 (提示:观察图形可以发现,每增加一个梯形,周长增加3);
(2)n=11时图形的周长是 .
20.如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,2 ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为

三、解答题
-
21.
已知:如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P在BC上运动,点P不与点B,C重合,设PC=x,若用y表示△APB的面积,求y与x的函数关系式,并求自变量x的取值范围.
 22.
22.乐平街上新开张了一家“好又多”超市,这个星期天,张明和妈妈去这家新开张的超市买东西,如图反映了张明从家到超市的时间t(分钟)与距离s(米)之间关系的一幅图:①图中反映了哪两个变量之间的关系?超市离家多远?②张明从家出发到达超市用了多少时间?从超市返回家花了多少时间?
③张明从家出发后20分钟到30分钟内可能在做什么?④张明从家到超市时的平均速度是多少?返回时的平均速度是多少?
 23. 在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值.
23. 在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值.所挂物体质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
18
20
22
24
26
28
(1)上述反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当所挂重物为3kg时,弹簧有多长?不挂重物呢?
(3)若所挂重物为6kg时(在弹簧的允许范围内),你能说出此时弹簧的长度吗?
四、综合题
-
24.
如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A、C在坐标轴上,点P在BC边上,直线l1:y=2x+3,直线l2:y=2x﹣3.
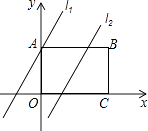 (1)、分别求直线l1与x轴,直线l2与AB的交点坐标;(2)、已知点M在第一象限,且是直线l2上的点,若△APM是等腰直角三角形,求点M的坐标;(3)、我们把直线l1和直线l2上的点所组成的图形为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且N点的横坐标为x,请直接写出x的取值范围(不用说明理由).25.
(1)、分别求直线l1与x轴,直线l2与AB的交点坐标;(2)、已知点M在第一象限,且是直线l2上的点,若△APM是等腰直角三角形,求点M的坐标;(3)、我们把直线l1和直线l2上的点所组成的图形为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且N点的横坐标为x,请直接写出x的取值范围(不用说明理由).25.如图1,△ABC中,∠C=90°,线段DE在射线BC上,且DE=AC,线段DE沿射线BC运动,开始时,点D与点B重合,点D到达点C时运动停止,过点D作DF=DB,与射线BA相交于点F,过点E作BC的垂线,与射线BA相交于点G.设BD=x,四边形DEGF与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x≤m,1<x≤m,m<x≤3时,函数的解析式不同)
 (1)、填空:BC的长是;(2)、求S关于x的函数关系式,并写出x的取值范围.26.
(1)、填空:BC的长是;(2)、求S关于x的函数关系式,并写出x的取值范围.26.如图1,B(2m,0),C(3m,0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD,使AB=2BC,画射线OA,把△ADC绕点C逆时针旋转90°得△A′D′C′,连接ED′,抛物线y=ax2+bx+n(a≠0)过E,A′两点.
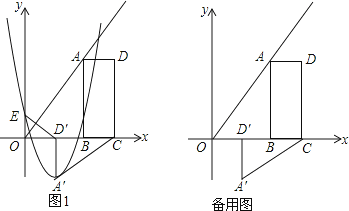 (1)、填空:∠AOB= °,用m表示点A′的坐标:A′( , );(2)、当抛物线的顶点为A′,抛物线与线段AB交于点P,且=时,△D′OE与△ABC是否相似?说明理由;(3)、若E与原点O重合,抛物线与射线OA的另一个交点为点M,过M作MN⊥y轴,垂足为N:
(1)、填空:∠AOB= °,用m表示点A′的坐标:A′( , );(2)、当抛物线的顶点为A′,抛物线与线段AB交于点P,且=时,△D′OE与△ABC是否相似?说明理由;(3)、若E与原点O重合,抛物线与射线OA的另一个交点为点M,过M作MN⊥y轴,垂足为N:①求a,b,m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为10,请你探究a的取值范围.