中考备考专题复习:一元一次不等式(组)
试卷更新日期:2017-02-07 类型:二轮复习
一、单选题
-
1. 已知点(1-2a , a-4)在第三象限,则整数a的值可以取( )个.
A、1 B、2 C、3 D、42. 不等式组 的解集是( )A、x>﹣2 B、x<1 C、﹣1<x<2 D、﹣2<x<13. 不等式组 的解集是x>1,则m的取值范围是( )
A、m≥1 B、m≤1 C、m≥0 D、m≤04. 对于不等式组 下列说法正确的是( )
A、此不等式组无解 B、此不等式组有7个整数解 C、此不等式组的负整数解是﹣3,﹣2,﹣1 D、此不等式组的解集是﹣ <x≤25.实数a、b在数轴上的位置如图所示,下列各式成立的是( )
 A、 B、a﹣b>0 C、ab>0 D、a+b>06. 从﹣3,﹣1, ,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组 无解,且使关于x的分式方程 ﹣ =﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )A、﹣3 B、﹣2 C、﹣ D、7. 若满足不等式20<5﹣2(2+2x)<50的最大整数解为a,最小整数解为b,则a+b之值为何?( )A、﹣15 B、﹣16 C、﹣17 D、﹣188. 现用甲、乙两种运输车将46t抗旱物资运往灾区,甲种运输车载重5t,乙种运输车载重4t,安排车辆不超过10辆,则甲种运输车至少应安排( )A、4辆 B、5辆 C、6辆 D、7辆9. 有一根长40mm的金属棒,欲将其截成x根7mm长的小段和y根9mm长的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )A、x=1,y=3 B、x=3,y=2 C、x=4,y=1 D、x=2,y=310. 定义:点A(x,y)为平面直角坐标系内的点,若满足x=y,则把点A叫做“平衡点”.例如:M(1,1),N(﹣2,﹣2)都是“平衡点”.当﹣1≤x≤3时,直线y=2x+m上有“平衡点”,则m的取值范围是( )A、0≤m≤1 B、﹣3≤m≤1 C、﹣3≤m≤3 D、﹣1≤m≤011. 宜宾市某化工厂,现有A种原料52千克,B种原料64千克,现用这些原料生产甲、乙两种产品共20件.已知生产1件甲种产品需要A种原料3千克,B种原料2千克;生产1件乙种产品需要A种原料2千克,B种原料4千克,则生产方案的种数为( )A、4 B、5 C、6 D、712. “一方有难,八方支援”,雅安芦山4•20地震后,某单位为一中学捐赠了一批新桌椅,学校组织初一年级200名学生搬桌椅.规定一人一次搬两把椅子,两人一次搬一张桌子,每人限搬一次,最多可搬桌椅(一桌一椅为一套)的套数为( )A、60 B、70 C、80 D、9013. 关于x的不等式组 ,其解集在数轴上表示正确的是( )A、
A、 B、a﹣b>0 C、ab>0 D、a+b>06. 从﹣3,﹣1, ,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组 无解,且使关于x的分式方程 ﹣ =﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )A、﹣3 B、﹣2 C、﹣ D、7. 若满足不等式20<5﹣2(2+2x)<50的最大整数解为a,最小整数解为b,则a+b之值为何?( )A、﹣15 B、﹣16 C、﹣17 D、﹣188. 现用甲、乙两种运输车将46t抗旱物资运往灾区,甲种运输车载重5t,乙种运输车载重4t,安排车辆不超过10辆,则甲种运输车至少应安排( )A、4辆 B、5辆 C、6辆 D、7辆9. 有一根长40mm的金属棒,欲将其截成x根7mm长的小段和y根9mm长的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )A、x=1,y=3 B、x=3,y=2 C、x=4,y=1 D、x=2,y=310. 定义:点A(x,y)为平面直角坐标系内的点,若满足x=y,则把点A叫做“平衡点”.例如:M(1,1),N(﹣2,﹣2)都是“平衡点”.当﹣1≤x≤3时,直线y=2x+m上有“平衡点”,则m的取值范围是( )A、0≤m≤1 B、﹣3≤m≤1 C、﹣3≤m≤3 D、﹣1≤m≤011. 宜宾市某化工厂,现有A种原料52千克,B种原料64千克,现用这些原料生产甲、乙两种产品共20件.已知生产1件甲种产品需要A种原料3千克,B种原料2千克;生产1件乙种产品需要A种原料2千克,B种原料4千克,则生产方案的种数为( )A、4 B、5 C、6 D、712. “一方有难,八方支援”,雅安芦山4•20地震后,某单位为一中学捐赠了一批新桌椅,学校组织初一年级200名学生搬桌椅.规定一人一次搬两把椅子,两人一次搬一张桌子,每人限搬一次,最多可搬桌椅(一桌一椅为一套)的套数为( )A、60 B、70 C、80 D、9013. 关于x的不等式组 ,其解集在数轴上表示正确的是( )A、 B、
B、 C、
C、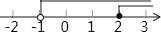 D、
D、 14.
14.运行程序如图所示,规定:从“输入一个值x”到“结果是否>95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( )
 A、x≥11 B、11≤x<23 C、11<x≤23 D、x≤2315. 表为小洁打算在某电信公司购买一支MAT手机与搭配一个门号的两种方案.此公司每个月收取通话费与月租费的方式如下:若通话费超过月租费,只收通话费;若通话费不超过月租费,只收月租费.若小洁每个月的通话费均为x元,x为400到600之间的整数,则在不考虑其他费用并使用两年的情况下,x至少为多少才会使得选择乙方案的总花费比甲方案便宜?( )
A、x≥11 B、11≤x<23 C、11<x≤23 D、x≤2315. 表为小洁打算在某电信公司购买一支MAT手机与搭配一个门号的两种方案.此公司每个月收取通话费与月租费的方式如下:若通话费超过月租费,只收通话费;若通话费不超过月租费,只收月租费.若小洁每个月的通话费均为x元,x为400到600之间的整数,则在不考虑其他费用并使用两年的情况下,x至少为多少才会使得选择乙方案的总花费比甲方案便宜?( )甲方案
乙方案
门号的月租费(元)
400
600
MAT手机价格(元)
15000
13000
注意事项:以上方案两年内不可变更月租费
A、500 B、516 C、517 D、600二、填空题
-
16. 关于x的一元二次方程x2+2x﹣2m+1=0的两实数根之积为负,则实数m的取值范围是 .
17. 不等式组 的最大整数解是 .18. 任取不等式组 的一个整数解,则能使关于x的方程:2x+k=﹣1的解为非负数的概率为 .
19. 若关于x的方程2x2+x﹣a=0有两个不相等的实数根,则实数a的取值范围是 .20. 当a、b满足条件a>b>0时, =1表示焦点在x轴上的椭圆.若 =1表示焦点在x轴上的椭圆,则m的取值范围是 .三、计算题
-
21.
解不等式组: , 并把解集在数轴上表示出来.
 22. x取哪些整数值时,不等式5x+2>3(x﹣1)与 x≤2﹣ 都成立?
22. x取哪些整数值时,不等式5x+2>3(x﹣1)与 x≤2﹣ 都成立?
23. 先化简,再求值:( ﹣1)÷ ,其中x的值从不等式组 的整数解中选取.
四、综合题
-
24. 某校准备组织师生共60人,从南靖乘动车前往厦门参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间
成人票价(元/张)
学生票价(元/张)
出发站
终点站
一等座
二等座
二等座
南靖
厦门
26
22
16
若师生均购买二等座票,则共需1020元.
(1)、参加活动的教师有人,学生有人;(2)、由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票全部费用为y元.①求y关于x的函数关系式;
②若购买一、二等座票全部费用不多于1032元,则提早前往的教师最多只能多少人?
25. 今年我市某公司分两次采购了一批大蒜,第一次花费40万元,第二次花费60万元.已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元,第二次采购时每吨大蒜的价格比去年的平均价格下降了500元,第二次的采购数量是第一次采购数量的两倍.(1)、试问去年每吨大蒜的平均价格是多少元?(2)、该公司可将大蒜加工成蒜粉或蒜片,若单独加工成蒜粉,每天可加工8吨大蒜,每吨大蒜获利1000元;若单独加工成蒜片,每天可加工12吨大蒜,每吨大蒜获利600元.由于出口需要,所有采购的大蒜必需在30天内加工完毕,且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半,为获得最大利润,应将多少吨大蒜加工成蒜粉?最大利润为多少?