中考备考专题复习：二次根式

试卷更新日期：2017-02-07 类型：二轮复习

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、3 $\sqrt{2}$ ﹣ $\sqrt{2}$ =3 B、a⁶÷a³=a² C、a²+a³=a⁵ D、（3a³）²=9a⁶

查看试题解析
2. 把 $\frac{\sqrt{3 a}}{\sqrt{12 a b}}$ 分母有理化后得（）

A、4b B、2 $\sqrt{b}$ C、 $\frac{1}{2}$ $\sqrt{b}$ D、 $\frac{\sqrt{b}}{2 b}$

查看试题解析
3. 若 $|x - 3 y| + \sqrt{y - 2} = 0$ ，则xy的值为（　　）

A、3 B、8 C、12 D、4

查看试题解析
4. 下列各式中，不是二次根式的是（）

A、 $\sqrt{2}$ B、 $\sqrt{3 - π}$ C、 $\sqrt{a^{2}}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
5. 已知：m，n是两个连续自然数（m＜n），且q=mn．设p= $\sqrt{q + n}$ + $\sqrt{q - m}$ ，则p( ).

A、总是奇数 B、总是偶数 C、有时是奇数，有时是偶数 D、有时是有理数，有时是无理数

查看试题解析
6. 对于任意的正数m、n定义运算※为：m※n= $\{\begin{matrix} \sqrt{m} - \sqrt{n} (m \geq n) \\ \sqrt{m} + \sqrt{n} (m < n) \end{matrix}$ ，计算（3※2）×（8※12）的结果为（　　）

A、2﹣4 $\sqrt{6}$ B、2 C、2 $\sqrt{5}$ D、20

查看试题解析
7. 若等腰三角形的两边长分别为 $\sqrt{50}$ 和 $\sqrt{72}$ ，则这个三角形的周长为（　　）

A、 $11 \sqrt{2}$ B、 $16 \sqrt{2}$ 或 $17 \sqrt{2}$ C、 $17 \sqrt{2}$ D、 $16 \sqrt{2}$

查看试题解析
8. 下列根式中，不是最简二次根式的是（）

A、 $\sqrt{10}$ B、 $\sqrt{8}$ C、 $\sqrt{6}$ D、 $\sqrt{2}$

查看试题解析
9. 下列等式一定成立的是（　　）

A、a²×a⁵=a¹⁰ B、 $\sqrt{a + b} = \sqrt{a} + \sqrt{b}$ C、（﹣a³）⁴=a¹² D、 $\sqrt{a^{2}} = a$

查看试题解析
10.
实数a，b在数轴上对应点的位置如图所示，化简|a|+ $\sqrt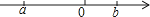{{(a - b)}^{2}}$ 的结果是（　　）

A、﹣2a+b B、2a﹣b C、﹣b D、b

查看试题解析
11. 与- $\sqrt{5}$ 是同类二次根式的是（　　）

A、 $\sqrt{10}$ B、 $\sqrt{15}$ C、 $\sqrt{20}$ D、 $\sqrt{25}$

查看试题解析
12. 二次根式 $\sqrt{2 - x}$ 有意义，则x的取值范围是（　　）

A、x＞2 B、x＜2 C、x≥2 D、x≤2

查看试题解析
13. 式子 $\frac{1}{\sqrt{x - 1}}$ 在实数范围内有意义，则x的取值范围是（）

A、x＜1 B、x≤1 C、x＞1 D、x≥1

查看试题解析
14. 若式子 $\sqrt{k- 1}$ +（k﹣1）⁰有意义，则一次函数y=（1﹣k）x+k﹣1的图象可能是（）

A、 B、 C、 D、

查看试题解析
15. 若1＜x＜2，则 $| x - 3 | + \sqrt{{(x - 1)}^{2}}$ 的值为（）

A、2x﹣4 B、﹣2 C、4﹣2x D、2

查看试题解析

二、填空题

16. 若 $|a - 2| + \sqrt{b - 3} + {(c - 4)}^{2} = 0$ ，则a-b+c= ．

查看试题解析
17. 若两个最简二次根式 $\sqrt{2 a}$ 与 $\sqrt{4 - 4 a}$ 可以合并，则a= ．

查看试题解析
18. 若代数式 $\frac{\sqrt{x - 1}}{x}$ 有意义，则x的取值范围是．

查看试题解析
19. 计算（ $\sqrt{5}$ + $\sqrt{3}$ ）（ $\sqrt{5}$ ﹣ $\sqrt{3}$ ）的结果等于．

查看试题解析
20. 如果整数x＞﹣3，那么使函数y= $\sqrt{π - 2 x}$ 有意义的x的值是（只填一个）

查看试题解析

三、计算题

21. 计算； $\sqrt{4}$ +2016⁰﹣| $\sqrt{3}$ ﹣2|+1．

查看试题解析
22. 计算： $| - \sqrt{2} | + \sqrt{9} \times {(\frac{1}{2})}^{- 1} - \sqrt{4} \times \sqrt{\frac{1}{2}} - {(π - 1)}^{0}$ ．

查看试题解析

四、解答题

23. 已知 $\sqrt{x - y + 3}$ + $\sqrt{x - 3}$ =0，求 $x y$ 的值.

查看试题解析
24.
实数a、b在数轴上的位置如图所示，化简： $\sqrt{a^{2}} - \sqrt{b^{2}} - \sqrt{{(a - b)}^{2}}$

查看试题解析
25. 我们知道，若两个有理数的积是1，则称这两个有理数互为倒数．同样的当两个实数 $(a + \sqrt{b})$ 与 $(a - \sqrt{b})$ 的积是1时，我们仍然称这两个实数互为倒数．
①判断 $(4 + \sqrt{2})$ 与 $(4 - \sqrt{2})$ 是否互为倒数，并说明理由；
②若实数 $(\sqrt{x} + \sqrt{y})$ 是 $(\sqrt{x} - \sqrt{y})$ 的倒数，求x和y之间的关系．

查看试题解析

五、综合题

26. 观察下列等式：
第1个等式：a₁= $\frac{1}{1 + \sqrt{2}}$ = $\sqrt{2}$ ﹣1，
第2个等式：a₂= $\frac{1}{\sqrt{2} + \sqrt{3}}$ = $\sqrt{3}$ ﹣ $\sqrt{2}$ ，
第3个等式：a₃= $\frac{1}{\sqrt{3} + 2}$ =2﹣ $\sqrt{3}$ ，
第4个等式：a₄= $\frac{1}{2 + \sqrt{5}}$ = $\sqrt{5}$ ﹣2，
按上述规律，回答以下问题：

(1)、请写出第n个等式：a_n=；

(2)、a₁+a₂+a₃+…+a_n= ．

查看试题解析
27. 已知任意三角形的三边长，如何求三角形面积？
古希腊的几何学家海伦解决了这个问题，在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S= $\sqrt{p (p - a) (p - b) (p - c)}$ （其中a，b，c是三角形的三边长，p= $\frac{a + b + c}{2}$ ，S为三角形的面积），并给出了证明
例如：在△ABC中，a=3，b=4，c=5，那么它的面积可以这样计算：
∵a=3，b=4，c=5
∴p= $\frac{a + b + c}{2}$ =6
∴S= $\sqrt{p (p - a) (p - b) (p - c)}$ = $\sqrt{6 \times 3 \times 2 \times 1}$ =6
事实上，对于已知三角形的三边长求三角形面积的问题，还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决．
如图，在△ABC中，BC=5，AC=6，AB=9

(1)、用海伦公式求△ABC的面积；

(2)、求△ABC的内切圆半径r．

查看试题解析