新人教版初中数学八年级下册 第十九章一次函数 19.3课题学习—选择方案 同步测试
试卷更新日期:2017-02-07 类型:同步测试
一、单选题
-
1.
小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(时)的函数图象如图所示.根据图象得到小亮结论,其中错误的是( )
 A、小亮骑自行车的平均速度是12km/h B、妈妈比小亮提前0.5小时到达姥姥家 C、妈妈在距家12km处追上小亮 D、9:30妈妈追上小亮2. 一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
A、小亮骑自行车的平均速度是12km/h B、妈妈比小亮提前0.5小时到达姥姥家 C、妈妈在距家12km处追上小亮 D、9:30妈妈追上小亮2. 一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:会员年卡类型
办卡费用(元)
每次游泳收费(元)
A 类
50
25
B 类
200
20
C 类
400
15
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( )
A、购买A类会员年卡 B、购买B类会员年卡 C、购买C类会员年卡 D、不购买会员年卡3.如图是小李销售某种食品的总利润y元与销售量x千克的函数图象(总利润=总销售额﹣总成本).由于目前销售不佳,小李想了两个解决方案:
方案(1)是不改变食品售价,减少总成本;
方案(2)是不改变总成本,提高食品售价.
下面给出的四个图象中虚线表示新的销售方式中利润与销售量的函数图象,则分别反映了方案(1)(2)的图象是( )
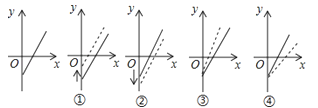 A、②,③ B、①,③ C、①,④ D、④,②4.
A、②,③ B、①,③ C、①,④ D、④,②4.随着互联网的发展,互联网消费逐渐深入人们生活,如图是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,下列说法:
(1)“快车”行驶里程不超过5公里计费8元;
(2)“顺风车”行驶里程超过2公里的部分,每公里计费1.2元;
(3)A点的坐标为(6.5,10.4);
(4)从哈尔滨西站到会展中心的里程是15公里,则“顺风车”要比“快车”少用3.4元,其中正确的个数有( )
 A、1个 B、2个 C、3个 D、4个5. 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,快车到达乙地后,快车停止运动,慢车继续以原速匀速驶往甲地,直至慢车到达甲地为止,设慢车行驶的时间为t(h),两车之间的距离为s(km),图中的折线表示s与t之间的函数关系.根据图象提供的信息有下列说法:①甲、乙两地之间的距离为900km;②行驶4h两车相遇;③快车的速度为150km/h;④行驶6h两车相距400km;⑤相遇时慢车行驶了240km;⑥快车共行驶了6h.其中符合图象描述的说法有( )个.
A、1个 B、2个 C、3个 D、4个5. 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,快车到达乙地后,快车停止运动,慢车继续以原速匀速驶往甲地,直至慢车到达甲地为止,设慢车行驶的时间为t(h),两车之间的距离为s(km),图中的折线表示s与t之间的函数关系.根据图象提供的信息有下列说法:①甲、乙两地之间的距离为900km;②行驶4h两车相遇;③快车的速度为150km/h;④行驶6h两车相距400km;⑤相遇时慢车行驶了240km;⑥快车共行驶了6h.其中符合图象描述的说法有( )个. A、3 B、4 C、5 D、66.
A、3 B、4 C、5 D、66.小亮和小明周六到距学校24km的滨湖湿地公园春游,小亮8:00从学校出发,骑自行车去湿地公园,小明8:30从学校出发,乘车沿相同路线去滨湖湿地公园,在同一直角坐标系中,小亮和小明的行进路程S(km)与时间t(时)的函数图象如图所示.根据图象得到结论,其中错误的是( )
 A、小亮骑自行车的平均速度是12km/h B、小明比小亮提前0.5小时到达滨湖湿地公园 C、小明在距学校12km处追上小亮 D、9:30小明与小亮相距4km7.
A、小亮骑自行车的平均速度是12km/h B、小明比小亮提前0.5小时到达滨湖湿地公园 C、小明在距学校12km处追上小亮 D、9:30小明与小亮相距4km7.在运动会径赛中,甲、乙同时起跑,刚跑出200m,甲不慎摔倒,他又迅速地爬起来继续投入比赛,若他们所跑的路程y(m)与比赛时间x(s)的关系如图,有下列说法:①他们进行的是800m比赛;②乙全程的平均速度为6.4m/s;③甲摔倒之前,乙的速度快;④甲再次投入比赛后的平均速度为7.5m/s;⑤甲再次投入比赛后在距离终点300米时追上了乙.其中正确的个数有( )
 A、2个 B、3个 C、4个 D、5个8. 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(甲车休息前后的速度相同),甲、乙两车行驶的路程y(km)与行驶的时间x(h)的函数图象如图所示.根据图象的信息有如下四个说法:
A、2个 B、3个 C、4个 D、5个8. 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(甲车休息前后的速度相同),甲、乙两车行驶的路程y(km)与行驶的时间x(h)的函数图象如图所示.根据图象的信息有如下四个说法:①甲车行驶40千米开始休息
②乙车行驶3.5小时与甲车相遇
③甲车比乙车晚2.5小时到到B地
④两车相距50km时乙车行驶了小时
其中正确的说法有( )
 A、1个 B、2个 C、3个 D、4个9.
A、1个 B、2个 C、3个 D、4个9.某车间接到加工一批零件的任务,准备派甲、乙两名工人参与完成.乙比甲晚参加工作一段时间,工作期间甲工人因有事停工5天,若两人分得的工作量相等,各自的工作效率一定,他们各自的工作量y(个)随工作时间x(天)变化的图象如图所示,则有下列说法:
(1)甲工人的工作效率为60个/天;
(2)乙工人每天比甲工人少生产10个零件;
(3)该车间接到的工作任务为生产零件300个;
(4)甲、乙两人实际生产时间相同.其中正确的个数是( )
 A、1个 B、2个 C、3个 D、4个10.
A、1个 B、2个 C、3个 D、4个10.如图是某电信公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,则下列结论中正确的共有( )
(1)若通话时间少于120分,则A方案比B方案便宜
(2)若通话时间超过200分,则B方案比A方案便宜
(3)若通讯费用为60元,则B方案比A方案的通话时间多
(4)当通话时间为170分钟时,A方案与B方案的费用相等.
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则购买盒子所需要最少费用为 元.
型号
A
B
单个盒子容量(升)
2
3
单价(元)
5
6
12. 如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省 元.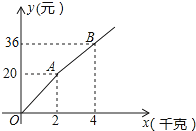 13. 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,
13. 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费.甲厂的总费用y1(干元)、乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示.
(l)甲厂的制版费为 千元,印刷费为平均每个 元,甲厂的费用yl与证书数量x之间的函数关系式为
(2)当印制证书数量不超过2千个时,乙厂的印刷费为平均每个 元;
(3)当印制证书数量超过2干个时,求乙厂的总费用y2与证书数量x之间的函数关系式
(4)若该单位需印制证书数量为8干个,该单位应选择 厂更节省费用.

三、解答题
-
14. 某农机租赁公司共有50台收割机,其中甲型20台、乙型30台,现将这50台联合收割机派往A、B两地区收割水稻,其中30台派往A地区,20台派往B地区,两地区与该农机公司商定的每天租赁价格如下表:
每台甲型收割机的租金
每台乙型收割机的租金
A地区
1800元
1600元
B地区
1600元
1200元
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y元,求y关于x的函数关系式;
(2)若使农机租赁公司这50台收割机一天所获租金不低于79600元,试写出满足条件的所有分派方案;
(3)农机租赁公司拟出一个分派方案,使该公司50台收割机每天获得租金最高,并说明理由.
15. 甲、乙两人沿同一路线登山,图中线段OC、折线OAB分别是甲、乙两人登山的路程y(米)与登山时间x(分)之间的函数图象.请根据图象所提供的信息,解答如下问题:(1)求甲登山的路程与登山时间之间的函数关系式,并写出自变量x的取值范围;
(2)求乙出发后多长时间追上甲?此时乙所走的路程是多少米?
 16. 为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分 的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.
16. 为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分 的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.
(1)观察图象求a,b,m的值
(2)直接写出y1 , y2与x之间的函数关系式;
(3)某旅行社导游王娜于5月1日带A团,5月20日(非节假日)带B团都到该景区旅游,共付门票款1900元,A,B两个团队合计50人,求A,B两个团队各有多少人?