江苏省镇江市2018届数学中考一模试卷

试卷更新日期：2018-07-18 类型：中考模拟

进入出卷网下载

一、单选题

1. 截止到2017年12月，全国移动互联网4G用户总数为947 000 000，这个数用科学记数法表示为（）

A、 $0.947 \times 10^{9}$ B、 $9.47 \times 10^{7}$ C、 $9.47 \times 10^{8}$ D、 $9.47 \times 10^{9}$

查看试题解析
2. 如图是由6个大小相同的小正方体组成的几何体，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 有一张平行四边形纸片ABCD，已知 $∠ B = 70^{°}$ ，按如图所示的方法折叠两次，则 $∠ B C F$ 的度数等于（）

A、55° B、50° C、45° D、40°

查看试题解析
4. 如图，一次函数 $y = k x + 3$ （ $k \neq 0$ ）的图像与正比例函数 $y = m x$ （ $m \neq 0$ ）的图像相交于点 $P$ ，已知点 $P$ 的横坐标为1，则关于 $x$ 的不等式 $(k - m) x > - 3$ 的解集为（）

A、 $x < 1$ B、 $1 < x < 2$ C、 $2 < x < 3$ D、 $x > 3$

查看试题解析
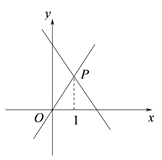5. 阅读：设试验结果落在某个区域S中每一点的机会均等，用A表示事件“试验结果落在S中的一个小区域M中”，那么事件A发生的概率P（A） $= \frac{M 的面积}{S 的面积}$ .在桌面上放一张50 cm×50 cm的正方形白纸ABCD，⊙O是它的内切圆，小明随机地将1000粒大米撒到该白纸上，其中落在圆内的大米有800粒，由此可得圆周率 $π$ 的值为（）

A、 $3 .1$ B、 $3 .2$ C、 $3 .14$ D、 $3 .15$

查看试题解析

二、填空题

6. $- \frac{1}{3}$ 的绝对值等于.

查看试题解析
7. 计算 ${(- 2)}^{2} \cdot {(- 2)}^{3}$ 的结果 = ．

查看试题解析
8. 分解因式： $x^{2} - 4 x + 3 =$ ．

查看试题解析
9. 使代数式 $\sqrt{1 - 2 x}$ 有意义的实数 $x$ 的取值范围是．

查看试题解析
10. 如图，l₁∥l₂ ， $Δ A B C$ 的顶点B、C在直线l₂上，已知∠A= $40^{°}$ ，∠1= $60^{°}$ ，则∠2的度数为．

查看试题解析
11. 已知一组数据－3，x，－2， 3，1，6的众数为3，则这组数据的中位数为．

查看试题解析
12. 用半径为10，圆心角为54°的扇形纸片围成一个圆锥的侧面，这个圆锥的底面圆半径等于．

查看试题解析
13. 已知DB是⊙C的直径，延长DB到点A，使得 $A B = \sqrt{10}$ ，PD为⊙C的切线，PD=CD，连接AP，若 $tan ∠ P A D = \frac{1}{3}$ ，则⊙C的半径长为．

查看试题解析
14. 如图，过原点O的直线与反比例函数 $y = \frac{k}{x} (k > 0)$ 的图像交于点A、P，过点P作x轴的垂线，点B为垂足，连接AB，若△ABP的面积是5，则 $k =$ ．

查看试题解析
15. 已知点 $A (1 ， y_{1})$ ， $B (m ， y_{2})$ 在二次函数 $y = x^{2} - 4 x + 1$ 的图像上，且 $y_{1} > y_{2}$ ，则实数m的取值范围是．

查看试题解析
16. 关于 $x$ 的一元二次方程 $4 x^{2} + 4 a x + a + 1 = 0$ 有两个相等的实数根，则 $\frac{a^{5} - 8 a}{a - 1}$ 的值等于．

查看试题解析
17. △ABC中，AB＝6，AC＝8，BC＝10，P为BC边上一动点，过线段AP上的点M作DE⊥AP，交边AB于点D，交边AC于点E，点N为DE中点，若四边形ADPE的面积为18，则AN的最大值= ．

查看试题解析

三、解答题

18.

(1)、计算： $（ - 2 ）^{- 1} + （ \sqrt{3} - 1 ）^{0} - sin 30 °$ ；

(2)、化简： $\frac{a + 1}{a^{2} - a} + \frac{1}{a}$

查看试题解析
19.

(1)、解方程： $\frac{x}{3 - x} = \frac{2}{x - 3} - 2$ ；

(2)、解不等式组： ${\begin{matrix} 2 (x + 2) > 3 x + 3 \\ \frac{x + 1}{4} + 1 < \frac{x}{3} \end{matrix}$

查看试题解析
20. 从甲、乙、丙三个厂家生产的同一种产品中各抽取8件产品，对其使用寿命进行跟踪调查，结果如下（单位：年）：
甲：3，4，5，6，8，8，8，10；
乙：4，6，6，6，8，9，12，13；
丙：3，3，4，7，9，10，11，12.

(1)、根据调查结果，三个厂家在广告中都称自己产品的使用寿命是8年，请分析他们各自的理由；

(2)、你认为哪个厂家的产品使用寿命更长一些？说说你的理由.

查看试题解析
21. 甲、乙二人用4张扑克牌（分别是红桃2，红桃3，黑桃4，方片5）玩游戏，他们将扑克牌洗匀后，背面朝上放在桌面上，甲先取一张，取出的牌不放回，乙从剩余的牌中取一张.

(1)、设 $i$ 、 $j$ 分别表示甲、乙取出的牌面上的数字，写出 $(i ， j)$ 的所有结果；

(2)、若甲取到红桃3，则乙取出的牌面数字比3大的概率是多少？

查看试题解析
22. 如图，在菱形ABCD中，AE⊥AD交BD于点E，CF⊥BC交BD于点F.

(1)、证明：△ADE≌△CBF ；

(2)、连接AF、CE，四边形AECF是菱形吗？说明理由．

查看试题解析
23. 如图，一次函数 $y = a x + b (a \neq 0)$ 与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像交于点 $P (2 ， m)$ 和点 $Q (- 8 ， m - 5)$ ，与x轴、y轴交于点A、B.

(1)、 $m =$ ， $k =$ ；

(2)、将线段AB沿x轴的正方向平移，使得点B的对应点恰好落在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像上，求平移的距离．

查看试题解析
24. 小明在广场的A 处放风筝，风筝线与水平线夹角为 $45^{0}$ ，此刻小丽在广场上距小明50米的B处观测小明的风筝，测得仰角为 $35^{0}$ ，求此时风筝距地面的高度.（结果精确到0.1m，小明、小丽的身高忽略不计）参考值： $sin 35^{°} \approx 0.57$ ， $cos 35^{°} \approx 0.82$ ， $tan 35^{°} \approx 0.70$ .

查看试题解析
25. 小丽的妈妈到水饺店买水饺，她手中的现金恰好只能买3两A类馅心的水饺或4两B类馅心的水饺，她准备买1斤水饺（A、B类馅心的水饺各半斤），于是向店家支付了手中的全部现金，再用电子支付的方式付了46元，求小丽妈妈手中的现金有多少元？

查看试题解析
26. 如图，A，B，C三点在⊙O上，直径BD平分∠ABC，过点D作DE∥AB交弦BC于点E，在BC的延长线上取一点F，使得EF $=$ DE．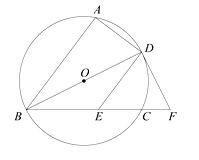

(1)、求证：DF是⊙O的切线；

(2)、连接AF交DE于点M，若 AD $=$ 4，DE $=$ 5，求DM的长．

查看试题解析
27. 如果过抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与y的交点作y轴的垂线与该抛物线有另一个交点，并且这两点与该抛物线的顶点构成正三角形，那么我们称这个抛物线为正三角抛物线．

(1)、抛物线 $y = 2 x^{2} + 3 \sqrt{3} x$ 正三角抛物线；（填“是”或“不是”）

(2)、如图，已知二次函数 $y = - x^{2} + 2 m x + 3 m^{2}$ （m > 0）的图像是正三角抛物线，它与x轴交于A、B两点(点A在点B的左侧)，点E在y轴上，当∠AEB=2∠ABE时，求出点E的坐标．

查看试题解析