江苏省扬州市江都区邵樊片2018届数学中考二模试卷

试卷更新日期：2018-07-18 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $| - 5 + 2 |$ 的结果是（）

A、3 B、2 C、-3 D、-2

查看试题解析
2. 下列各式计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $a^{4} \div a^{4} = a$ C、 ${(a^{3})}^{2} = a^{5}$ D、 $2 a^{2} - a^{2} = a^{2}$

查看试题解析
3. 如图是某个几何体的三视图，该几何体是（）

A、三棱柱 B、圆柱 C、六棱柱 D、圆锥

查看试题解析
4. 如果一个正多边形的内角和等于 $720 °$ ，那么该正多边形的一个外角等于（）

A、 $45 °$ B、 $60 °$ C、 $72 °$ D、 $90 °$

查看试题解析
5. 点A （4，3）经过某种图形变化后得到点B（-3，4），这种图形变化可以是（）

A、关于x轴对称 B、关于y轴对称 C、绕原点逆时针旋转90° D、绕原点顺时针旋转90°

查看试题解析
6. 如图，在Rt△ABC中，∠ACB = 90°，BC = 2．将△ABC绕顶点C逆时针旋转得到△ $A^{'} B^{'} C$ 使点 $B^{'}$ 落在AC边上．设M是 $A^{'} B^{'}$ 的中点，连接BM，CM，则△BCM的面积为（）

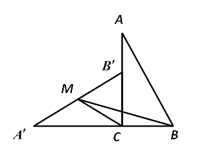A、1 B、2 C、3 D、4

查看试题解析
7. 对于点A（x₁ ， y₁），B（x₂ ， y₂），定义一种运算：A⊕B=（x₁+x₂）+（y₁+y₂）．例如，A（﹣5，4），B（2，﹣3），A⊕B=（﹣5+2）+（4﹣3）=﹣2．若互不重合的四点C，D，E，F，满足C⊕D=D⊕E=E⊕F=F⊕D，则C，D，E，F四点（）

A、在同一条直线上 B、在同一条抛物线上 C、在同一反比例函数图象上 D、是同一个正方形的四个顶点

查看试题解析
8. 如图，在△ABC中，∠C＝90°，点D是BC边上一动点，过点B作BE⊥AD交AD的延长线于E．若AC＝6，BC＝8，则 $\frac{D E}{A D}$ 的最大值为（ )

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{3}{4}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析

二、填空题

9. 据统计，2018年扬州五一黄金周共接待游客约3500000人次，数据“3500000”用科学记数法可表示为．

查看试题解析
10. 若式子 $\sqrt{x + \frac{1}{3}}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
11. 已知： $a^{2} + a = 4$ ，则代数式 $a (2 a + 1) - (a + 2) (a - 2)$ 的值是．

查看试题解析
12. 如图，四边形ABCD是平行四边形，⊙O经过点A，C，D，与BC交于点E，连接AE，若∠D =72°，则∠BAE =°．

查看试题解析
13. 已知一组数据1，a，3，6，7，它的平均数是4，这组数据的方差是．

查看试题解析
14. 点A（a，b）是一次函数y=x﹣2与反比例函数y= $\frac{4}{x}$ 的交点，则a²b﹣ab²= ．

查看试题解析
15. 圆锥的母线长为11cm，侧面积为33πcm² ，圆锥的底面圆的半径为．

查看试题解析
16. 如图，G为△ABC的重心，DE过点G，且DE∥BC，交AB、AC，分别于D、E两点，若△ADE的面积为5，则四边形BDEC的面积为．

查看试题解析
17. 如图，矩形ABCD中，E是AC的中点，点A、B在x轴上．若函数 $y = \frac{8}{x}$ （ $x > 0$ ）的图像过D、E两点，则矩形ABCD的面积为．

查看试题解析
18. 如图，已知点A是第一象限内横坐标为 $\sqrt{3}$ 的一个定点，AC⊥x轴于点M，交直线y=﹣x于点N．若点P是线段ON上的一个动点，∠APB=30°，BA⊥PA，则点P在线段ON上运动时，A点不变，B点随之运动．求当点P从点O运动到点N时，点B运动的路径长是．

查看试题解析

三、解答题

19.

(1)、计算： ${(\sqrt{15} - π)}^{0} + {(- \frac{1}{2})}^{- 2} - 2 sin 30 ° - | \sqrt{3} - 2 |$

(2)、解不等式组： ${\begin{matrix} x - 3 (x - 2) \leq 4 \\ \frac{x - 1}{2} < \frac{x + 1}{3} \end{matrix}$

查看试题解析
20. 先化简，再求值： $(\frac{3}{x + 1} - x + 1) \div \frac{x^{2} - 2 x}{x + 1}$ ，其中-2 x 2，请从x的范围中选入一个你喜欢的值代入，求此分式的值.

查看试题解析
21. 某区教育局为了解今年九年级学生体育测试情况，随机抽查了某班学生的体育测试成绩为样本，按A、B、C、D四个等级进行统计，并将统计结果绘制成如下的统计图，请你结合图中所给信息解答下列问题：
说明：A级：90分～100分；B级：75分～89分；C级：60分～74分；D级：60分以下

(1)、样本中D级的学生人数占全班学生人数的百分比是；

(2)、扇形统计图中A级所在的扇形的圆心角度数是；

(3)、请把条形统计图补充完整；

(4)、若该校九年级有500名学生，请你用此样本估计体育测试中A级和B级的学生人数之和.

查看试题解析
22. 聪聪参加我市电视台组织的“阳光杯”智力竞答节目，答对最后两道单选题就顺利通关，第一道单选题有 $3$ 个选项，第二道单选题有4个选项，这两道题聪聪都不会，不过聪聪还有两个“求助”可以用（使用“求助”一次可以让主持人去掉其中一题的一个错误选项）．

(1)、如果聪聪两次“求助”都在第一道题中使用，那么聪聪通关的概率是．

(2)、如果聪聪将每道题各用一次“求助”，请用树状图或者列表来分析他顺利通关的概率．

查看试题解析
23. 如图：在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线交BC于点E（尺规作图的痕迹保留在图中了），连接EF．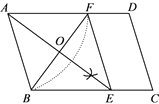

(1)、求证：四边形ABEF为菱形；

(2)、AE，BF相交于点O，若BF=6，AB=5，求AE的长．

查看试题解析
24. 几个小伙伴打算去音乐厅观看演出，他们准备用350元购买门票．下面是两个小伙伴的对话：小芳：今天看演出，如果我们每人一张票，会差两张票的钱.
小明：过两天就是“儿童节”了，到时票价会打七折，我们每人一张票，还能剩35元钱呢！根据对话的内容，请你求出小伙伴们的人数．

查看试题解析
25. 有一只拉杆式旅行箱（图1），其侧面示意图如图2所示．已知箱体长AB=50cm，拉杆 $B C$ 的伸长距离最大时可达35cm，点A，B，C在同一条直线上．在箱体底端装有圆形的滚轮⊙A，⊙A与水平地面MN相切于点D．在拉杆伸长至最大的情况下，当点B距离水平地面38cm时，点C到水平地面的距离CE为59cm．
设AF∥MN．

(1)、求⊙A的半径长；

(2)、当人的手自然下垂拉旅行箱时，人感到较为舒服．某人将手自然下垂在C端拉旅行箱时，CE为80cm， $∠ C A F$ =64°．求此时拉杆BC的伸长距离．（精确到1cm，参考数据： $sin 64 ° \approx 0.90$ ， $cos 64 ° \approx 0.39$ ， $tan 64 ° \approx 2.1$ ）

查看试题解析
26. 如图，四边形 $A B C D$ 是矩形，点 $P$ 是对角线 $A C$ 上一动点(不与 $A$ 、 $C$ 重合)，连接 $P B$ ，过点 $P$ 作 $P E ⊥ P B$ ，交射线 $D C$ 于点 $E$ ，已知 $A D = 3$ ， $A B = 4$ .

(1)、求 $\frac{P E}{P B}$ 的值；

(2)、当 $Δ P C E$ 是以PC为底的等腰三角形时.请求出AP的值；

查看试题解析
27. 对于⊙P及一个矩形给出如下定义：如果⊙P上存在到此矩形四个顶点距离都相等的点，那么称⊙P是该矩形的“等距圆”．如图，在平面直角坐标系xOy中，矩形ABCD的顶点A的坐标为（ $\sqrt{3}$ ， $2$ ），顶点C、D在x轴上，且OC=OD.

(1)、当⊙P的半径为4时，
①在P₁（ $0$ ， $- 3$ ），P₂（ $2 \sqrt{3}$ ， $3$ ），P₃（ $- 2 \sqrt{3}$ ， $1$ ）中可以成为矩形ABCD的“等距圆”的圆心的是；
②如果点P在直线 $y = - \frac{\sqrt{3}}{3} x + 1$ 上，且⊙P是矩形ABCD的“等距圆”，求点P的坐标；

(2)、已知点P在 $y$ 轴上，且⊙P是矩形ABCD的“等距圆”，如果⊙P与直线AD没有公共点，直接写出点P的纵坐标m的取值范围. （2）点P在y上，且⊙P是矩形ABCD的“等距圆”，且⊙P与直线AD没有公共点，得出|m-1|＜ $\sqrt{3}$ ，且|m-1|≠0，求解即可得出m的取值范围，即点P的纵坐标的取值范围

查看试题解析
28. 如图，在平面直角坐标系xOy中，抛物线 $y = a x^{2} + b x + 3$ 与 $x$ 轴交于点A（-3，0），C（1，0），与 $y$ 轴交于点B.

(1)、求此抛物线的解析式；

(2)、点P是直线AB上方的抛物线上一动点（不与点A，B重合），过点P作 $x$ 轴的垂线，垂足交点为F，交直线AB于点E，作 $P D ⊥ A B$ 于点D.
①点P在什么位置时，△PDE的周长最大，求出此时P点的坐标；
②连接PA，以PA为边作正方形APMN，当顶点M或N恰好落在抛物线对称轴上时，求出对应的P点的坐标．

查看试题解析