江苏省苏州市2018届数学中考模拟试卷
试卷更新日期:2018-07-18 类型:中考模拟
一、单选题
-
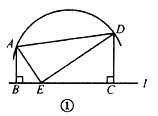
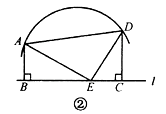
1. -0.5的倒数是( )A、 B、 C、-2 D、22. 下列计算正确的是( )A、 B、 C、 D、3. 在平面直角坐标系中,若P( , )在第二象限,则 的取值范围是( )A、 B、 C、 D、4. 如图,在梯形 中, ,中位线 与对角线 交于 两点,若 cm, cm,则 的长等于( )
 A、10 cm B、13 cm C、20 cm D、26 cm5. 经过圆锥顶点的截面的形状可能是( )A、
A、10 cm B、13 cm C、20 cm D、26 cm5. 经过圆锥顶点的截面的形状可能是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,在矩形纸片 中, ,点 在边 上,将 沿直线 折叠,点 恰好落在对角线 上的点 处,若 ,则 的长是( )
6. 如图,在矩形纸片 中, ,点 在边 上,将 沿直线 折叠,点 恰好落在对角线 上的点 处,若 ,则 的长是( )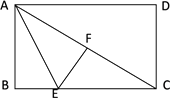 A、 B、6 C、4 D、57. 函数y=ax2+1的图像经过点(-2,0),则 的方程 的实数根为( )A、 , B、 , C、 , D、 ,8. 如图,在 中, 是 的中点,将 沿 翻折得到 ,连接 ,则线段 的长等于( )
A、 B、6 C、4 D、57. 函数y=ax2+1的图像经过点(-2,0),则 的方程 的实数根为( )A、 , B、 , C、 , D、 ,8. 如图,在 中, 是 的中点,将 沿 翻折得到 ,连接 ,则线段 的长等于( ) A、2 B、 C、 D、9. 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为 的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM= EF,则正方形ABCD的面积为( )
A、2 B、 C、 D、9. 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为 的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM= EF,则正方形ABCD的面积为( ) A、 B、 C、 D、10. 我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧 , , ,…得到斐波那契螺旋线,然后顺次连结 , , ,…得到螺旋折线(如图),已知点 (0,1), ( ,0), (0, ),则该折线上的点 的坐标为( )
A、 B、 C、 D、10. 我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧 , , ,…得到斐波那契螺旋线,然后顺次连结 , , ,…得到螺旋折线(如图),已知点 (0,1), ( ,0), (0, ),则该折线上的点 的坐标为( ) A、( ,24) B、( ,25) C、( ,24) D、( ,25)
A、( ,24) B、( ,25) C、( ,24) D、( ,25)二、填空题
-
11. 已知方程组 的解为 ,则2a-3b的值为 .
12. 在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1=° 13. 已知⊙ 和⊙ 的半径分别是一元二次方程 的两根,且 ,则⊙ 和⊙ 的位置关系是.14. 若关于x的分式方程 有增根,则实数m的值是 .
13. 已知⊙ 和⊙ 的半径分别是一元二次方程 的两根,且 ,则⊙ 和⊙ 的位置关系是.14. 若关于x的分式方程 有增根,则实数m的值是 .
15. 小明要用圆心角为120°,半径是27 cm的扇形纸片(如图)围成一个圆锥形纸帽,做成后这个纸帽的底面直径为cm.(不计接缝部分,材料不剩余) 16. 如图,已知 是线段 的黄金分割点,且 .若 表示以 为一边的正方形的面积, 表示长是 、宽是 的矩形的面积,则 .(填“>”“=”或“<”)
16. 如图,已知 是线段 的黄金分割点,且 .若 表示以 为一边的正方形的面积, 表示长是 、宽是 的矩形的面积,则 .(填“>”“=”或“<”) 17. 如图,在平面内,线段AB=6,P为线段AB上的动点,三角形纸片CDE的边CD所在的直线与线段AB垂直相交于点P,且满足PC=PA.若点P沿AB方向从点A运动到点B,则点E运动的路径长为 .
17. 如图,在平面内,线段AB=6,P为线段AB上的动点,三角形纸片CDE的边CD所在的直线与线段AB垂直相交于点P,且满足PC=PA.若点P沿AB方向从点A运动到点B,则点E运动的路径长为 .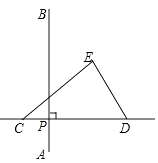 18. 如图,已知点 是一次函数 图像上一点,过点 作 轴的垂线 是 上一点( 在 上方),在 的右侧以 为斜边作等腰直角三角形 ,反比例函数 的图像过点 ,若 的面积为6,则 的面积是.
18. 如图,已知点 是一次函数 图像上一点,过点 作 轴的垂线 是 上一点( 在 上方),在 的右侧以 为斜边作等腰直角三角形 ,反比例函数 的图像过点 ,若 的面积为6,则 的面积是.
三、解答题
-
19. 计算: .20. 解不等式组: .21. 先化简,再计算: 其中 .22. 用A4纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.设在同一家复印店一次复印文件的页数为 ( 为非负整数).
(1)、根据题意,填写下表:一次复印页数(页)
5
10
20
30
…
甲复印店收费(元)
2
…
乙复印店收费(元)
…
(2)、设在甲复印店复印收费 元,在乙复印店复印收费 元,分别写出 关于 的函数关系式;
(3)、当 时,顾客在哪家复印店复印花费少?请说明理由.23. “低碳环保,你我同行”,市区的公共自行车给市民出行带来不少方便,我校数学社团小学员走进小区随机选取了市民进行调查,调查的问题是“您大概多久使用一次公共自行车?”,将本次调查结果归为四种情况:A.每天都用 B.经常使用 C.偶尔使用 D.从未使用
将这次调查情况整理并绘制出如下两幅统计图:

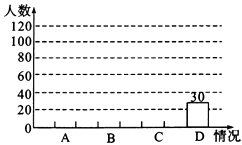
根据图中的信息,解答下列问题:
(1)、本次活动共有位市民参与调查;(2)、补全条形统计图;(3)、根据统计结果,若市区有26万市民,请估算每天都用公共自行车的市民约有多少人.
24. 如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC. (1)、求证:△ADE∽△ABC;(2)、若AD=3,AB=5,求 的值.25. 小强与小刚都住在安康小区,在同一所学校读书,某天早上,小强7:30从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留2分钟,校车行驶途中始终保持匀速.当天早上,小刚7:39从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早1分钟到学校站点,他们乘坐的车辆从安康小区站出发所行驶路程y(千米)与行驶时间x(分钟)之间的函数图象如图所示.
(1)、求证:△ADE∽△ABC;(2)、若AD=3,AB=5,求 的值.25. 小强与小刚都住在安康小区,在同一所学校读书,某天早上,小强7:30从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留2分钟,校车行驶途中始终保持匀速.当天早上,小刚7:39从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早1分钟到学校站点,他们乘坐的车辆从安康小区站出发所行驶路程y(千米)与行驶时间x(分钟)之间的函数图象如图所示.
(1)、求点A的纵坐标m的值;(2)、小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车?并求此时他们距学校站点的路程.
26. 如图①,某超市从一楼到二楼的电梯 的长为16. 50 m,坡角 为32°. (1)、求一楼与二楼之间的高度 (精确到0. 01 m) ;(2)、电梯每级的水平级宽均是0.25m,如图②,小明跨上电梯时,该电梯以每秒上升2级
(1)、求一楼与二楼之间的高度 (精确到0. 01 m) ;(2)、电梯每级的水平级宽均是0.25m,如图②,小明跨上电梯时,该电梯以每秒上升2级的高度运行,10s后他上升了多少米?
(精确到0. 01 m,参考数据: )