新人教版初中数学九年级下册 第二十六章反比例函数 26.2实际问题与反比例函数 同步测试
试卷更新日期:2017-02-06 类型:同步测试
一、单选题
-
1. 一个圆柱的侧面展开图是一个面积为4的矩形,这个圆柱的母线l与圆柱的底面半径r之间的函数关系是( )
A、正比例函数 B、反比例函数 C、一次函数 D、二次函数2. 已知广州市的土地总面积约为7434 km2 , 人均占有的土地面积S(单位:km2/人)随全市人口n(单位:人)的变化而变化,则S与n的函数关系式为( )A、S=7434n B、S= C、n=7434S D、S=3.在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图所示,当V=10m3时,气体的密度是( )
 A、5kg/m3 B、2kg/m3 C、100kg/m3 D、1kg/m34. 已知甲、乙两地相距20千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )A、t=20v B、t= C、t= D、t=5. 下列两个变量之间的关系为反比例关系的是( )A、匀速行驶过程中,行驶路程与时间的关系 B、体积一定时,物体的质量与密度的关系 C、质量一定时,物体的体积与密度的关系 D、长方形的长一定时,它的周长与宽的关系6. 某工厂现有原材料100吨,每天平均用去x吨,这批原材料能用y天,则y与x之间的函数表达式为( )A、y=100x B、y= C、y=+100 D、y=100﹣x7.
A、5kg/m3 B、2kg/m3 C、100kg/m3 D、1kg/m34. 已知甲、乙两地相距20千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )A、t=20v B、t= C、t= D、t=5. 下列两个变量之间的关系为反比例关系的是( )A、匀速行驶过程中,行驶路程与时间的关系 B、体积一定时,物体的质量与密度的关系 C、质量一定时,物体的体积与密度的关系 D、长方形的长一定时,它的周长与宽的关系6. 某工厂现有原材料100吨,每天平均用去x吨,这批原材料能用y天,则y与x之间的函数表达式为( )A、y=100x B、y= C、y=+100 D、y=100﹣x7.一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系: , 其图象为如图所示的一段曲线,且端点为和 , 若行驶速度不得超过60(km/h),则汽车通过该路段最少需要时间为( )
 A、分 B、40分 C、60分 D、分8. 如果以12m3/h的速度向水箱进水,5h可以注满.为了赶时间,现增加进水管,使进水速度达到Q(m3/h),那么此时注满水箱所需要的时间t(h)与Q(m3/h)之间的函数关系为( )A、t= B、t=60Q C、t=12﹣ D、t=12+9. 面积为2的直角三角形一直角边长为x,另一直角边长为y,则y与x的变化规律用图象大致表示为( )A、
A、分 B、40分 C、60分 D、分8. 如果以12m3/h的速度向水箱进水,5h可以注满.为了赶时间,现增加进水管,使进水速度达到Q(m3/h),那么此时注满水箱所需要的时间t(h)与Q(m3/h)之间的函数关系为( )A、t= B、t=60Q C、t=12﹣ D、t=12+9. 面积为2的直角三角形一直角边长为x,另一直角边长为y,则y与x的变化规律用图象大致表示为( )A、 B、
B、 C、
C、 D、
D、 10.
10.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:25)能喝到不小于70℃的水,则接通电源的时间可以是当天上午的( )
 A、7:00 B、7:10 C、7:25 D、7:3511. 设从泉港到福州乘坐汽车所需的时间是t(小时),汽车的平均速度为v(千米/时),则下面大致能反映v与t的函数关系的图象是( )A、
A、7:00 B、7:10 C、7:25 D、7:3511. 设从泉港到福州乘坐汽车所需的时间是t(小时),汽车的平均速度为v(千米/时),则下面大致能反映v与t的函数关系的图象是( )A、 B、
B、 C、
C、 D、
D、 12.
12.某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,水温从100℃降到35℃所用的时间是( )
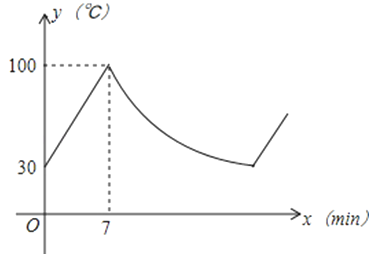 A、27分钟 B、20分钟 C、13分钟 D、7分钟13.
A、27分钟 B、20分钟 C、13分钟 D、7分钟13.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
 A、小于1.25m3 B、大于1.25m3 C、不小于0.8m3 D、大于0.8m314. 三角形的面积为12cm2 , 这时底边上的高ycm底边xcm之间的函数关系用图象表示大致是( )A、
A、小于1.25m3 B、大于1.25m3 C、不小于0.8m3 D、大于0.8m314. 三角形的面积为12cm2 , 这时底边上的高ycm底边xcm之间的函数关系用图象表示大致是( )A、 B、
B、 C、
C、 D、
D、 15.
15.已知一块蓄电池的电压为定值,以此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图,则电流I关于电阻R的函数解析式为( )
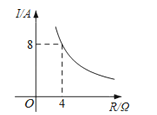 A、I= B、I= C、I= D、I=-
A、I= B、I= C、I= D、I=-二、填空题
-
16. 乳韶公路全长为38km,一辆汽车以每小时vkm从乳源开往韶关,则所需时间t(h)与汽车速度v(km/h)之间的函数关系式是: .
17. 一辆汽车行驶在一段全程为100千米的高速公路上,那么这辆汽车行完全程所需的时间y(小时)与它的速度x(千米/小时)之间的关系式为y= .18. 因为有人造谣:碘盐可以预防核辐射,导致人们抢购碘盐,造成碘盐价格波动.一个人准备用100元到市场上购买碘盐,则购买数量y(千克)与价格x(元/千克)的关系为19. 把一个长、宽、高分别为3cm,2cm,1cm的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积s(cm2)与高h(cm)之间的函数关系式为 .
20. 某高科技开发公司从2008年起开始投入技术改进资金,经过技术改进后,其产品的生产成本不断降低,具体数据如下表:请你认真分析表中数据,写出可以表示该变化规律的表达式是年 度
2008
2009
2010
2011
投入技术改进资金x(万元)
2.5
3
4
4.5
产品成本y(万元∕件)
7.2
6
4.5
4
三、解答题
-
21. 已知一个长方体的体积是100cm3 , 它的长是ycm,宽是10cm,高是xcm.
(1)写出y与x之间的函数关系式;
(2)当x=2cm时,求y的值.
22.为了预防流感,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图),现测药物8分钟燃毕,此时空气中每立方米含药量为6毫克,请根据题中所提供的信息,回答下列问题

(1)药物燃烧时,y关于x的函数关系式为 , 自变量x的取值范围是 ;药物燃烧完后,y与x的函数关系式为 ;
(2)研究表明,当空气中的每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过几分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效地杀灭空气中的病菌,那么此次消毒是否有效?为什么?23.家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反比例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻随温度升高而增加,温度每上升1℃,电阻增加kΩ.
(1)求当10≤t≤30时,R和t之间的关系式;
(2)求温度在30℃时电阻R的值;并求出t≥30时,R和t之间的关系式;
(3)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过6 kΩ?
 24.
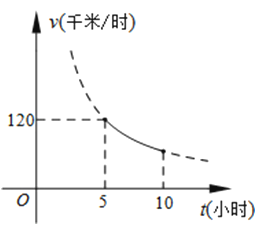
24.一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)直接写出v与t的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站A、B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.
 25.
25.如图,一次函数y=kx+b的图象与反比例函数y=(x>0)的图象交于P(n,2),与x轴交于A(﹣4,0),与y轴交于C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)反比例函数图象有一点D,使得以B、C、P、D为顶点的四边形是菱形,求出点D的坐标.
