江苏省南京市秦淮区2018届数学中考一模试卷

试卷更新日期：2018-07-18 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $\sqrt{{(- 3)}^{2}}$ 的结果是（）

A、3 B、 $- 3$ C、9 D、 $- 9$

查看试题解析
2. 据某数据库统计，仅2018年第一个月，区块链行业融资额就达到680 000 000元．将680 000 000用科学记数法表示为（）

A、0.68×10⁹ B、6.8×10⁷ C、6.8×10⁸ D、6.8×10⁹

查看试题解析
3. 下列计算正确的是（）

A、a³ $+$ a² $=$ a⁵ B、a¹⁰ $\div$ a² $=$ a⁵ C、(a²)³ $=$ a⁵ D、a² $\cdot$ a³ $=$ a⁵

查看试题解析
4. 某校航模兴趣小组共有30位同学，他们的年龄分布如下表：
年龄/岁
13
14
15
16
人数
5
15
由于表格污损，15和16岁人数不清，则下列关于年龄的统计量可以确定的是（）

A、平均数、中位数 B、众数、中位数 C、平均数、方差 D、中位数、方差

查看试题解析
5. 将二次函数 $y = - x^{2}$ 的图像向右平移2个单位长度，再向上平移3个单位长度，所得图像的函数表达式为（）

A、 $y = - {(x - 2)}^{2} + 3$ B、 $y = - {(x - 2)}^{2} - 3$ C、 $y = - {(x + 2)}^{2} + 3$ D、 $y = - {(x + 2)}^{2} - 3$

查看试题解析
6. 如图，在平面直角坐标系中，▱ABCD的顶点坐标分别为A(3.6，a)，B(2，2)，C(b，3.4)，D(8，6)，则 $a + b$ 的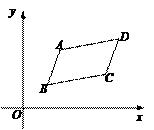值为（）

A、8 B、9 C、10 D、11

查看试题解析

二、填空题

7. -3的相反数是；-3的倒数是

查看试题解析
8. 若式子 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
9. 计算 $\frac{\sqrt{3} \times \sqrt{12}}{\sqrt{2}}$ 的结果是．

查看试题解析
10. 方程 $\frac{1}{x - 2} = \frac{3}{x}$ 的解是．

查看试题解析
11. 若关于x的一元二次方程的两个根x₁ ， x₂满足 $x_{1} + x_{2} = 3$ ， $x_{1} x_{2} = 2$ ，则这个方程是．（写出一个符合要求的方程）

查看试题解析
12. 将函数y=x的图像绕坐标原点O顺时针旋转90°，所得图像的函数表达式为．

查看试题解析
13. 已知⊙O的半径为10，弦AB∥CD，AB=12，CD=16，则AB和CD的距离为．

查看试题解析
14. 如图，在△ABC中，∠A $=$ 70°，∠B $=$ 55°，以BC为直径作⊙O，分别交AB、AC于点E、F，则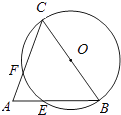 $\overset{⌢}{E F}$ 的度数为°．

查看试题解析
15. 如图，在正方形ABCD中，E是BC上一点，BE $= \frac{1}{3}$ BC，连接AE，作BF⊥AE，分别与AE、CD交于点K、F，G、H分别在AD、AE上，且四边形KFGH是矩形，则 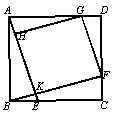$\frac{H G}{A B} =$ ．

查看试题解析

三、解答题

16. 在照明系统模拟控制电路实验中，研究人员发现光敏电阻值R（单位：Ω）与光照度E（单位：lx）之间成反比例函数关系，部分数据如下表所示，则光敏电阻值R与光照度E的函数表达式为．
光照度E/lx
0.5
1
1.5
2
2.5
3
光敏电阻阻值R/Ω
60
30
20
15
12
10

查看试题解析
17. 计算 $(\frac{1}{a - b} - \frac{b}{a^{2} - b^{2}}) \div \frac{a}{a + b}$ ．

查看试题解析
18. 解一元二次不等式 $x^{2} - 4 > 0$ ．
请按照下面的步骤，完成本题的解答．
解： $x^{2} - 4 > 0$ 可化为 $(x + 2) (x - 2) > 0$ ．

(1)、依据“两数相乘，同号得正”，可得不等式组① ${\begin{matrix} x + 2 > 0 \\ x - 2 > 0 \end{matrix}$ 或不等式组② ．

(2)、解不等式组①，得．

(3)、解不等式组②，得．

(4)、一元二次不等式 $x^{2} - 4 > 0$ 的解集为．

查看试题解析
19. 已知关于x的一元二次方程 ${(x - m)}^{2} - 2 (x - m) = 0$ (m为常数)．

(1)、求证：不论m为何值，该方程总有两个不相等的实数根；

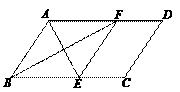
(2)、若该方程一个根为3，求m的值．

查看试题解析
20. 如图，在▱ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F，连接EF．
求证：四边形ABEF是菱形．

查看试题解析
21. 中国的茶文化源远流长，根据制作方法和茶多酚氧化（发酵）程度的不同，可分为六大类：绿茶（不发酵）、白茶（轻微发酵）、黄茶（轻发酵）、青茶（半发酵）、黑茶（后发酵）、红茶（全发酵）．春节将至，为款待亲朋好友，小叶去茶庄选购茶叶．茶庄有碧螺春、龙井两种绿茶，一种青茶——武夷岩茶及一种黄茶——银针出售．

(1)、随机购买一种茶叶，是绿茶的概率为；

(2)、随机购买两种茶叶，求一种是绿茶、一种是银针的概率．

查看试题解析
22. 如图，甲、乙两人在一次射击比赛中击中靶的情况（击中靶中心“×”所在的圆面为10环，靶中各数字表示该数所在圆环被击中所得的环数），每人射击了6次．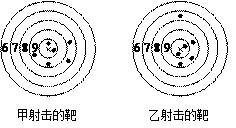

(1)、请用列表法将他俩的射击成绩统计出来；

(2)、请你运用所学的统计知识做出分析，从两个不同角度评价甲、乙两人的打靶成绩．

查看试题解析
23. 某商场在“双十一”促销活动中决定对购买空调的顾客实行现金返利．规定每购买一台空调，商场返利若干元．经调查，销售空调数量y₁（单位：台）与返利x（单位：元）之间的函数表达式为 $y_{1} = x + 800$ ．每台空调的利润y₂（单位：元）与返利x的函数图象如图所示．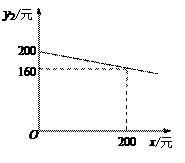

(1)、求y₂与x之间的函数表达式；

(2)、每台空调返利多少元才能使销售空调的总利润最大？最大总利润是多少？

查看试题解析
24. 一铁棒欲通过一个直角走廊．如图，是该铁棒紧挨着墙角E通过时的两个特殊位置：当铁棒位于AB位置时，它与墙面OG所成的角∠ABO $=$ 51°18′；当铁棒底端B向上滑动1m(即BD $=$ 1m)到达CD位置时，它与墙面OG所成的角∠CDO $=$ 60°，求铁棒的长．（参考数据：sin51°18′ $\approx$ 0.780，cos51°18′ $\approx$ 0.625，tan51°18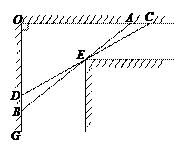′ $\approx$ 1.248）

查看试题解析
25. 如图，在Rt△ABC中，∠C $=$ 90°，AC $=$ BC，AD是△ABC的角平分线，以D为圆心，DC为半径作⊙D，交AD于点E．

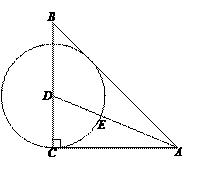(1)、判断直线AB与⊙D的位置关系并证明．

(2)、若AC $=$ 1，求的长．

查看试题解析
26. 书籍开本有数学开本指书刊幅面的规格大小．如图①，将一张矩形印刷用纸对折后可以得到2开纸，再对折得到4开纸，以此类推可以得到8开纸、16开纸……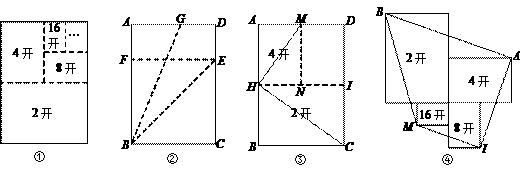
若这张矩形印刷用纸的短边长为a．

(1)、如图②，若将这张矩形印刷用纸ABCD(AB $>$ BC)进行折叠，使得BC与AB重合，点C落在点F处，得到折痕BE；展开后，再次折叠该纸，使点A落在E处，此时折痕恰好经过点B，得到折痕BG，求 $\frac{A B}{B C}$ 的值．

(2)、如图③，2开纸BCIH和4开纸AMNH的对角线分别是HC、HM．说明HC⊥HM．

(3)、将图①中的2开纸、4开纸、8开纸和16开纸按如图④所示的方式摆放，依次连接点A、B、M、I，则四边形ABMI的面积是.（用含a的代数式表示，直接写出结果）

查看试题解析
27. 【数学概念】
若四边形ABCD的四条边满足AB $\cdot$ CD $=$ AD $\cdot$ BC，则称四边形ABCD是和谐四边形．

(1)、【特例辨别】
下列四边形：①平行四边形，②矩形，③菱形，④正方形．其中一定是和谐四边形的是．

(2)、【概念判定】
如图①，过⊙O外一点P引圆的两条切线PS、PT，切点分别为A、C，过点P 作一条射线PM，分别交⊙O于点B、D，连接AB、BC、CD、DA．求证：四边形ABCD是和谐四边形．

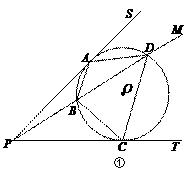(3)、【知识应用】
如图②，CD是⊙O的直径，和谐四边形ABCD内接于⊙O，且BC $=$ AD．请直接写出AB与CD的关系．

查看试题解析

年龄/岁	13	14	15	16
人数	5	15

光照度E/lx	0.5	1	1.5	2	2.5	3
光敏电阻阻值R/Ω	60	30	20	15	12	10