江苏省连云港市灌云县2018届数学中考一模试卷
试卷更新日期:2018-07-18 类型:中考模拟
一、单选题
-
1. 比2小1的数是A、3 B、1 C、 D、02. 下列计算正确的是
A、 B、 C、 D、3. 若式子 有意义,在实数范围内有意义,则x的取值范围是
A、 B、 C、 D、4. 一个物体的从不同方向看到的是如图所示的三个图形,则该物体的形状为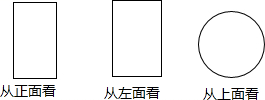 A、圆柱体 B、棱柱 C、圆锥 D、长方体5. 该校22名男子足球队队员的年龄分布情况如下表:
A、圆柱体 B、棱柱 C、圆锥 D、长方体5. 该校22名男子足球队队员的年龄分布情况如下表:年龄 岁
13
14
15
16
17
18
频数 人数
2
6
8
3
2
1
则这些队员年龄的平均数和中位数分别是(
A、16岁、15岁 B、15岁、14岁 C、14岁、15岁 D、15岁、15岁6. 若二次函数 的x与y的部分对应值如下表:x
0
1
2
y
8
3
0
0
则抛物线的顶点坐标是
A、 B、 C、 D、7. 如图,长方形纸片的宽为1,沿直线BC折叠,得到重合部分 , ,则 的面积为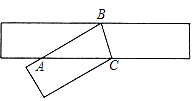 A、1 B、2 C、 D、8. 如图,已知 ,相邻两条平行直线间的距离相等,若等腰直角 的直角顶点C在 上,另两个顶点A,B分别在 、 上,则 的值是
A、1 B、2 C、 D、8. 如图,已知 ,相邻两条平行直线间的距离相等,若等腰直角 的直角顶点C在 上,另两个顶点A,B分别在 、 上,则 的值是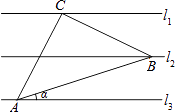 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 钓鱼岛是中国的固有领土,位于中国东海,面积约4400000平方米,数据4400000用科学记数法表示为 .10. 在元旦晚会的投飞镖游戏环节中,5名同学的投掷成绩 单位:环 分别是:7、9、9、6、8,则这组数据的众数是 .
11. 某暗箱中放有10个形状大小一样的球,其中有三个红球、若干个白球和蓝球,若从中任取一个是白球的概率为 ,则蓝球的个数是 .
12. 分解因式: .
13. 如图, ,点B在直线b上,且 ,若 ,则 的大小为 .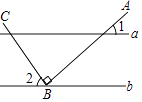 14. 如图,在 中, , , ,将 绕点A按顺时针旋转一定角度得到 ,当点B的对应点D恰好落在BC边上时,则CD的长为 .
14. 如图,在 中, , , ,将 绕点A按顺时针旋转一定角度得到 ,当点B的对应点D恰好落在BC边上时,则CD的长为 .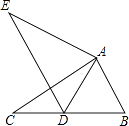 15. 如图,矩形ABCD中, , ,CE是 的平分线与边AB的交点,则BE的长为 .
15. 如图,矩形ABCD中, , ,CE是 的平分线与边AB的交点,则BE的长为 .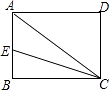 16. 如图,在平面直角坐标系中, 的边 轴,点A在双曲线 上,点B在双曲线 上,边AC中点D在x轴上, 的面积为8,则 .
16. 如图,在平面直角坐标系中, 的边 轴,点A在双曲线 上,点B在双曲线 上,边AC中点D在x轴上, 的面积为8,则 .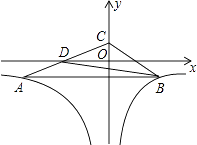
三、解答题
-
17. 化简:
18. 解方程: .19. 计算: .20. 某校为了了解九年级学生体育测试成绩情况,以九年级 班学生的体育测试成绩为样本,按A,B,C,D四个等级进行统计,并将结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题: 说明:A级: 分;B级: 分;C级: 分;D级:60分以下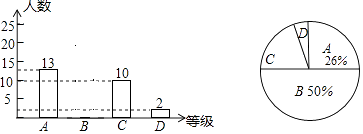 (1)、写出D级学生的人数占全班总人数的百分比为 , C级学生所在的扇形圆心角的度数为;
(1)、写出D级学生的人数占全班总人数的百分比为 , C级学生所在的扇形圆心角的度数为;
(2)、补全条形图;
(3)、若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?
21. 某商场为了吸引顾客,设计了一种促销活动:在四等分的转盘上依次标有“0元”、“10元”、“30元”、“50元”字样,购物每满300元可以转动转盘2次,每次转盘停下后,顾客可以获得指针所指区域相应金额的购物券 指针落在分界线上不计次数,可重新转动一次 ,一个顾客刚好消费300元,并参加促销活动,转了2次转盘.
(1)、求出该顾客可能落得购物券的最高金额和最低金额;
(2)、请用列表法或画树状图法求出该顾客获购物金额不低于50元的概率.
22. 如图,将▱ABCD的边AB延长至点E,使 ,连接DE、EC,DE交BC于点O.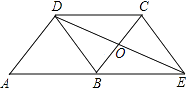 (1)、求证: ≌ ;
(1)、求证: ≌ ;
(2)、连接BD,若 ,试判断四边形DBEC的形状,并说明理由.23. 近年来,共享单车服务的推出 如图 ,极大的方便了城市公民绿色出行,图2是某品牌某型号单车的车架新投放时的示意图 车轮半径约为 ,其中 直线l, , .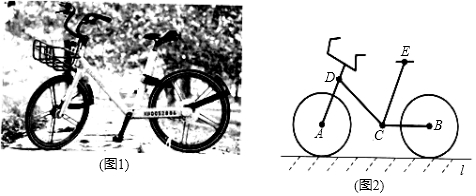
参考数据: , ,
(1)、求单车车座E到地面的高度; 结果精确到
(2)、根据经验,当车座E到CB的距离调整至等于人体胯高 腿长 的 时,坐骑比较舒适 小明的胯高为70cm,现将车座E调整至座椅舒适高度位置 ,求 的长 结果精确到
24. 如图,D为 上一点,点C在直径BA的延长线上,且 .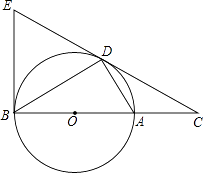 (1)、判断直线CD与 的位置关系,并说明理由.(2)、过点B作的 切线交CD的延长线于点E,若
(1)、判断直线CD与 的位置关系,并说明理由.(2)、过点B作的 切线交CD的延长线于点E,若 ,
,  ,求 的半径长. 25. 某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
,求 的半径长. 25. 某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:商品名称
甲
乙
进价 元 件
40
90
售价 元 件
60
120
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(1)、写出y关于x的函数关系式:
(2)、该商品计划最多投入8000元用于购买者两种商品,则至少要购进多少件甲商品?若销售完这些商品,则商场可获得的最大利润是多少元?
(3)、实际进货时,生产厂家对甲种商品的出厂价下调a元 出售 且限定商场最多购购进甲种商品60件,若商场保持同种商品的售价不变,请你根据以上信息及 中条件,设计出使该商场获得最大利润的进货方案.
26. 如图,已知抛物线 经过点 和点 ,点C为抛物线与y轴的交点.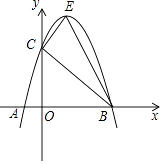 (1)、求抛物线的解析式;(2)、若点E为直线BC上方抛物线上的一点,请求出 面积的最大值.(3)、在 条件下,是否存在这样的点 ,使得 为等腰三角形?如果有,请直接写出点D的坐标;如果没有,请说明理由.27. 如图
(1)、求抛物线的解析式;(2)、若点E为直线BC上方抛物线上的一点,请求出 面积的最大值.(3)、在 条件下,是否存在这样的点 ,使得 为等腰三角形?如果有,请直接写出点D的坐标;如果没有,请说明理由.27. 如图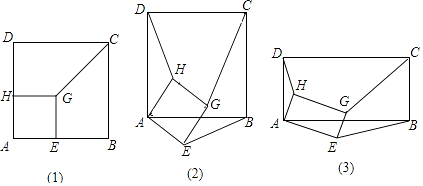 (1)、如图 ,正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD:GC:EB的结果;(2)、将图 中的正方形AEGH绕点A旋转一定角度,如图 ,求HD:GC:EB;(3)、把图 中的正方形都换成矩形,如图 ,且已知DA: : ,求此时HD:GC:EB的值 简要写出过程 .
(1)、如图 ,正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD:GC:EB的结果;(2)、将图 中的正方形AEGH绕点A旋转一定角度,如图 ,求HD:GC:EB;(3)、把图 中的正方形都换成矩形,如图 ,且已知DA: : ,求此时HD:GC:EB的值 简要写出过程 .