江苏省淮安市清江浦区2018届数学中考二模试卷

试卷更新日期：2018-07-18 类型：中考模拟

进入出卷网下载

一、单选题

1. $- 2018$ 的倒数是（）

A、 $2018$ B、 $- 2018$ C、 $\frac{1}{2018}$ D、 $- \frac{1}{2018}$

查看试题解析
2. 点A在数轴上表示+2，从A点沿数轴向左平移3个单位到点B，则点B所表示的数是（）

A、﹣1 B、3 C、5 D、﹣1 或3

查看试题解析
3. 某班7名女生的体重（单位：kg）分别是35、37、38、40、42、42、74，这组数据的众数是（）

A、40 B、42 C、44 D、74

查看试题解析
4. 从2013年到2017年，这五年间我国脱贫攻坚取得重大进展，全国贫困人口减少68000000，数据68000000用科学记数法表示为（）

A、 $0.68 \times 10^{8}$ B、 $68 \times 10^{6}$ C、 $6.8 \times 10^{7}$ D、 $680 \times 10^{5}$

查看试题解析
5. 某村耕地总面积为50公顷，且该村人均耕地面积y（单位：公顷/人）与总人口x（单位：人）的函数图象如图所示，则下列说法正确的是（）

A、该村人均耕地面积随总人口的增多而增多 B、该村人均耕地面积y与总人口x成正比例 C、若该村人均耕地面积为2公顷，则总人口有100人 D、当该村总人口为50人时，人均耕地面积为1公顷

查看试题解析
6. 如图，AB是⊙O的直径，直线PA与⊙O相切于点A，PO交⊙O于点C，连接BC．若∠P = 40°，则∠ABC的度数为（）

A、25° B、35° C、40° D、50°

查看试题解析
7. 如图，矩形ABCD的顶点A、C分别在直线a、b上，且a∥b，∠1=60°，则∠2的度数为（）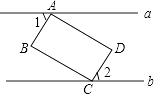

A、30° B、45° C、60° D、75°

查看试题解析

二、填空题

8. 正五边形的外角和等于 ◦．

查看试题解析
9. 分解因式： $5 x^{3} - 10 x^{2} + 5 x$ = ．

查看试题解析
10. 分式方程 $\frac{3}{x + 1}$ = $\frac{2}{x}$ 的解是．

查看试题解析
11. 若 ${(x - \sqrt{7})}^{0}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 在一次数学测试中，某班50名学生的成绩分为六组，第一组到第四组的频数分别为6，8，9，12，第五组的频率是0.2，则第六组的频数是．

查看试题解析
13. 如图，已知圆锥的底面⊙O的直径BC=6，高OA=4，则该圆锥的侧面展开图的面积为．

查看试题解析
14. 如图，在正方形ABCD的外侧，作等边三角形CDE，连接AE，BE，则∠AEB的度数为◦

查看试题解析

三、解答题

15.

(1)、计算： ${(\frac{1}{2})}^{- 2}$ + $| 2 - \sqrt{3} |$ +2sin60°

(2)、解不等式组： ${\begin{matrix} x - 1 \geq 0 \\ \frac{1}{2} (x + 4) \leq 3 \end{matrix}$

查看试题解析
16. 已知： $2 a^{2} + 3 a - 6 = 0$ 求代数式 $3 a (2 a + 1) - (2 a + 1) (2 a - 1)$ 的值．

查看试题解析
17. 《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．它的代数成就主要包括开放术、正负术和方程术．其中，方程术是《九章算术》最高的数学成就．《九章算术》中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两．问牛、羊各直金几何？”
译文：“假设有5头牛、2只羊，值金10两；2头牛、5只羊，值金8两．问每头牛、每只羊各值金多少两？”

查看试题解析
18. 如图，⊙O是Rt△ABC的外接圆，∠ACB=90°，∠A=25°，过点C作⊙O的切线，交AB的延长线于点D，求∠D的度数．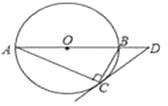

查看试题解析
19. 在平面直角坐标系xOy中，直线 $y = k x + b$ $(k \neq 0)$ 与双曲线 $y = \frac{8}{x}$ 的一个交点为P（2，m），与x轴、y轴分别交于点A，B．

(1)、求m的值；

(2)、若PA=2AB，求k的值．

查看试题解析
20. 在平行四边形ABCD中，过点D作DE⊥AB于点E，点F 在边CD上，DF=BE，连接AF，BF．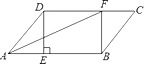

(1)、求证：四边形BFDE是矩形；

(2)、若CF=3，BF=4，DF=5，求证：AF平分∠DAB．

查看试题解析
21. 如图，Rt△ABC中，∠C=90°，AC= $\sqrt{5}$ ，tanB= $\frac{1}{2}$ ．半径为2的⊙C，分别交AC、BC于点D、E，得到 $\vec{D E}$ .

(1)、求证：AB为⊙C的切线；

(2)、求图中阴影部分的面积.

查看试题解析
22. 一个不透明袋子中有1个红球，1个绿球和n个白球，这些球除颜色外无其他差别．

(1)、当n =1时，从袋中随机摸出1个球，摸到红球与摸到白球的可能性是否相同？（在答题卡相应位置填“相同”或“不相同”）

(2)、从袋中随机摸出1个球，记录其颜色，然后放回．大量重复该实验，发现摸到绿球的频率稳定于0.25，则n的值是；

(3)、在一个摸球游戏中，所有可能出现的结果如下：
根据树状图呈现的结果，求两次摸出的球颜色不同的概率．

查看试题解析
23. 有这样一个问题：探究函数 $y = \frac{1}{2} x^{2} + \frac{1}{x}$ 的图象与性质．
小东根据学习函数的经验，对函数 $y = \frac{1}{2} x^{2} + \frac{1}{x}$ 的图象与性质进行了探究．
下面是小东的探究过程，请补充完整：

(1)、函数 $y = \frac{1}{2} x^{2} + \frac{1}{x}$ 的自变量x的取值范围是；

(2)、下表是y与x的几组对应值．
x
…
﹣3
﹣2
﹣1
﹣ $\frac{1}{2}$
﹣ $\frac{1}{3}$
$\frac{1}{3}$
$\frac{1}{2}$
1
2
3
…
y
…
$\frac{25}{6}$
$\frac{3}{2}$
﹣ $\frac{1}{2}$
$\frac{15}{8}$
$\frac{53}{18}$
$\frac{55}{18}$
$\frac{17}{18}$
$\frac{3}{2}$
$\frac{5}{2}$
m
…
求m的值；

(3)、如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；

(4)、进一步探究发现，该函数图象在第一象限内的最低点的坐标是（1， $\frac{3}{2}$ ），结合函数的图象，写出该函数的其它性质（一条即可）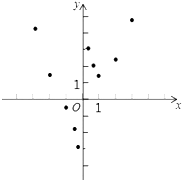

查看试题解析
24. 如图，抛物线 $y = a x^{2} + b x + 5$ $(a \neq 0)$ 与直线 $y = x + 1$ 相交于A（﹣1 ，0），B（4 ，m）两点，且与x轴交于A 、C两点．

(1)、求抛物线的解析式；

(2)、点P是抛物线上的一个动点（不与点A、点B重合），过点P作直线PD⊥x轴于点D，交直线AB于点E．
① 当PE = 2ED时，求P点坐标；
② 是否存在点P使△BEC为等腰三角形？若存在请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析