新人教版初中数学九年级下册 第二十六章反比例函数 26.1.2反比例函数的图象和性质 同步测试
试卷更新日期:2017-02-06 类型:同步测试
一、单选题
-
1. 下列各点不在反比例函数y=的图象上的应是( )
A、(6,-2) B、(6,2) C、(3,4) D、(-3,-4)2. 如果反比例函数的图像经过点(-1,2),那么这个反比例函数的图象一定经过点( )
A、( , 2); B、( , 2); C、(2,-1); D、(-2,-1).3. 如图,反比例函数的图象经过点A(-1,-2).则当x>1时,函数值y的取值范围是( )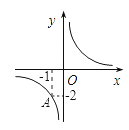 A、y>1 B、0<y<1 C、y>2 D、0< y<24. 如果反比例函数y=的图象经过点(-1,-2),则k的值是( )A、2 B、-2 C、-3 D、35. 如图,双曲线y=的一个分支为( )
A、y>1 B、0<y<1 C、y>2 D、0< y<24. 如果反比例函数y=的图象经过点(-1,-2),则k的值是( )A、2 B、-2 C、-3 D、35. 如图,双曲线y=的一个分支为( )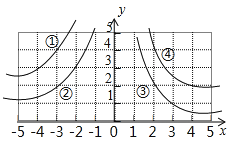 A、① B、② C、③ D、④6. 已知反比例函数的图象经过点(-1,2),则它的解析式是( )A、 B、 C、 D、7. 如图是我们学过的反比例函数图象,它的函数解析式可能是( )
A、① B、② C、③ D、④6. 已知反比例函数的图象经过点(-1,2),则它的解析式是( )A、 B、 C、 D、7. 如图是我们学过的反比例函数图象,它的函数解析式可能是( )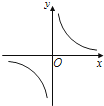 A、 B、 C、 D、y=8. 如图,矩形AOBC的面积为4,反比例函数的图象的一支经过矩形对角线的交点P,则该反比例函数的解析式是
A、 B、 C、 D、y=8. 如图,矩形AOBC的面积为4,反比例函数的图象的一支经过矩形对角线的交点P,则该反比例函数的解析式是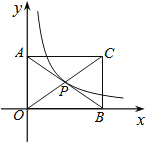 A、 B、 C、 D、9. 已知点P(-1,3)在反比例函数的图象上,则k的值是 ( )A、 B、 C、3 D、-310. 下列图象中是反比例函数 图象的是( )A、
A、 B、 C、 D、9. 已知点P(-1,3)在反比例函数的图象上,则k的值是 ( )A、 B、 C、3 D、-310. 下列图象中是反比例函数 图象的是( )A、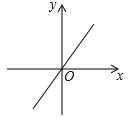 B、
B、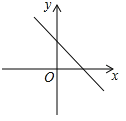 C、
C、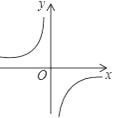 D、
D、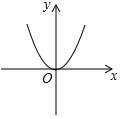 11. 某反比例函数象经过点(-1,6),则下列各点中此函数图象也经过的是( )A、(-3,2) B、(3,2) C、(2,3) D、(6,1)12. 如图,点A在双曲线y= 上,点B在双曲线y= (k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是8,则k的值为( )
11. 某反比例函数象经过点(-1,6),则下列各点中此函数图象也经过的是( )A、(-3,2) B、(3,2) C、(2,3) D、(6,1)12. 如图,点A在双曲线y= 上,点B在双曲线y= (k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是8,则k的值为( )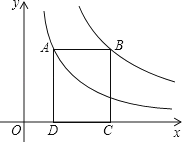 A、12 B、10 C、8 D、613. 如图,在平面直角坐标系中,点A是双曲线y=(x>0)上的一个动点,过点A作x轴的垂线,交x轴于点B,点A运动过程中△AOB的面积将会( )
A、12 B、10 C、8 D、613. 如图,在平面直角坐标系中,点A是双曲线y=(x>0)上的一个动点,过点A作x轴的垂线,交x轴于点B,点A运动过程中△AOB的面积将会( )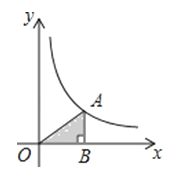 A、逐渐增大 B、逐渐减小 C、先增大后减小 D、不变14. 已知反比例函数y=的图象如图所示,则实数m的取值范围是( )
A、逐渐增大 B、逐渐减小 C、先增大后减小 D、不变14. 已知反比例函数y=的图象如图所示,则实数m的取值范围是( )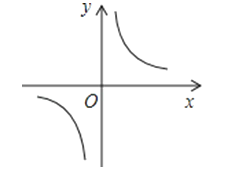 A、m>1 B、m>0 C、m<1 D、m<015. 若点A(﹣5,y1),B(﹣3,y2),C(2,y3)在反比例函数y= 的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y3<y2 B、y1<y2<y3 C、y3<y2<y1 D、y2<y1<y3
A、m>1 B、m>0 C、m<1 D、m<015. 若点A(﹣5,y1),B(﹣3,y2),C(2,y3)在反比例函数y= 的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y3<y2 B、y1<y2<y3 C、y3<y2<y1 D、y2<y1<y3二、填空题
-
16. 已知A(﹣1,m)与B(2,m﹣3)是反比例函数图象上的两个点.则m的值 .
17. 某种灯的使用寿命为8000小时,那么它可使用的天数y与平均每天使用的小时数x之间的函数关系式为 .18. 圆柱的体积为10cm3 , 则它的高ycm与底面积xcm2之间的函数关系式是 .19. 某商场出售一批进价为2元的贺卡,在市场营销中发现此贺卡的日销售单价x(元)与日销售量y(个)之间有如下关系:日销售单价x(元)
…
3
4
5
6
…
日销售量y(个)
…
20
15
12
10
…
则y与x之间的函数关系式为 .
20. 如图所示,反比例函数y= (k≠0,x>0)的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为8,则k的值为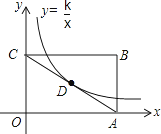
三、解答题
-
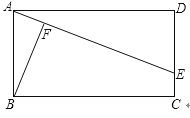
21. 如图,E为矩形ABCD的边CD上的一个动点,BF⊥AE于F,AB=2,BC=4,设AE=x,BF=y,求y与x之间的关系式,并写出x的取值范围.
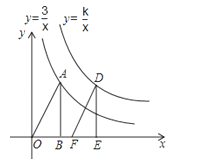
 22. 如图,点A(1,a)在反比例函数y=(x>0)的图象上,AB垂直于x轴,垂足为点B,将△ABO沿x轴向右平移2个单位长度,得到Rt△DEF,点D落在反比例函数y=(x>0)的图象上.
22. 如图,点A(1,a)在反比例函数y=(x>0)的图象上,AB垂直于x轴,垂足为点B,将△ABO沿x轴向右平移2个单位长度,得到Rt△DEF,点D落在反比例函数y=(x>0)的图象上.(1)求点A的坐标;
(2)求k值.
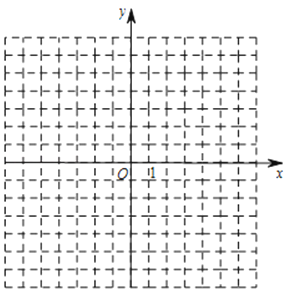
 23. 画出函数y=的图象.
23. 画出函数y=的图象.(1)完成下列表格:
x
…
﹣6
﹣5
﹣4
﹣3
﹣2
﹣1
1
2
3
4
5
6
…
y=
…
﹣1
﹣1.5
﹣2
6
3
2
1.2
1
…
(2)描点,画图.
 24. 已知一个长方体的体积是100cm3 , 它的长是ycm,宽是10cm,高是xcm.
24. 已知一个长方体的体积是100cm3 , 它的长是ycm,宽是10cm,高是xcm.(1)写出y与x之间的函数关系式;
(2)当x=2cm时,求y的值.
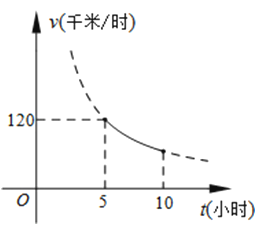
25. 一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.(1)直接写出v与t的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站A、B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.