江苏省常州市武进区2018届数学中考一模试卷
试卷更新日期:2018-07-18 类型:中考模拟
一、单选题
-
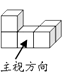
1. ﹣6的绝对值是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 2017年常州市实现地区生产总值约6622亿元,将6622用科学记数法表示为( )A、 B、 C、 D、5. 已知:甲乙两组数据的平均数都是3,甲组数据的方差 ,乙组数据的方差 ,下列结论中正确的是( )A、甲组数据比乙组数据的波动性大 B、甲组数据的比乙组数据的波动性小 C、甲组数据与乙组数据的波动性一样大 D、甲组数据与乙组数据的波动性无法比较6. 若点A(x,y)是第二象限内的点,则下列不等式中一定成立的是( )A、 B、 C、 D、7. 如图,▱ABCD中,AC=3cm,BD=5cm,则边AD的长可以是( )
4. 2017年常州市实现地区生产总值约6622亿元,将6622用科学记数法表示为( )A、 B、 C、 D、5. 已知:甲乙两组数据的平均数都是3,甲组数据的方差 ,乙组数据的方差 ,下列结论中正确的是( )A、甲组数据比乙组数据的波动性大 B、甲组数据的比乙组数据的波动性小 C、甲组数据与乙组数据的波动性一样大 D、甲组数据与乙组数据的波动性无法比较6. 若点A(x,y)是第二象限内的点,则下列不等式中一定成立的是( )A、 B、 C、 D、7. 如图,▱ABCD中,AC=3cm,BD=5cm,则边AD的长可以是( )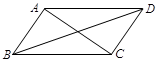 A、3cm B、4cm C、5cm D、6cm8. 如右图,正方形ABCD的边长为2,点E是BC边上一点,以AB为直径在正方形内作半圆O,将△DCE沿DE翻折,点C刚好落在半圆O的点F处,则CE的长为( )
A、3cm B、4cm C、5cm D、6cm8. 如右图,正方形ABCD的边长为2,点E是BC边上一点,以AB为直径在正方形内作半圆O,将△DCE沿DE翻折,点C刚好落在半圆O的点F处,则CE的长为( )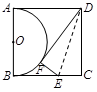 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 计算: .10. 若分式 有意义,则x的取值范围是 .11. 分解因式: .12. 已知扇形的半径为8 cm,圆心角为45°,则此扇形的弧长是cm.
13. 一个多边形的内角和比它的外角和大900°,则这个多边形的边数是.14. 已知关于 的方程 的一个根是1,则另一个根为 .15. 一根长为2米的笔直的木棍直立在地面上,某一时刻,它在太阳光下的投影长为2.4米.在同一时刻,站立在地面上的小强的影子长为2.1米,则小强的身高为米
16. 如图,四边形ABCD内接于⊙O,OC∥AD,∠DAB=60°,∠ADC=106°,则∠OCB=°. 17. 已知x,y满足 ,当 时,y的取值范围是.18. 如图,在平面直角坐标系xOy中,点B(-1,4),点A(-7,0),点P是直线 上一点,且∠ABP=45°,则点P的坐标为.
17. 已知x,y满足 ,当 时,y的取值范围是.18. 如图,在平面直角坐标系xOy中,点B(-1,4),点A(-7,0),点P是直线 上一点,且∠ABP=45°,则点P的坐标为.
三、解答题
-
19. 先化简,再求值: ,其中 .
20. 解方程和不等式组:
(1)、(2)、21. 随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”、“了解”、“了解较少”、“不了解”四类,并将检查结果绘制成下面两个统计图.
 (1)、本次调查的学生共有人,“了解较少”的学生人数所占的百分比为;(2)、补全条形统计图;(3)、若该校共有1300名学生,请根据统计结果估算该校“不了解”的学生人数.22. 如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
(1)、本次调查的学生共有人,“了解较少”的学生人数所占的百分比为;(2)、补全条形统计图;(3)、若该校共有1300名学生,请根据统计结果估算该校“不了解”的学生人数.22. 如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等. (1)、随机转动转盘一次,停止后(若指针落在分割线上,则重新转动,直至指向数字),指针指向数字1的概率是多少?(直接写出结果)(2)、小丽和小芳利用此转盘做游戏,游戏规则如下:自由转动转盘两次(若指针落在分割线上,则重转,直至指向数字),如果指针两次所指的数字之和为偶数,则小丽胜;否则,小芳胜.你认为对双方公平吗?请说明理由.
(1)、随机转动转盘一次,停止后(若指针落在分割线上,则重新转动,直至指向数字),指针指向数字1的概率是多少?(直接写出结果)(2)、小丽和小芳利用此转盘做游戏,游戏规则如下:自由转动转盘两次(若指针落在分割线上,则重转,直至指向数字),如果指针两次所指的数字之和为偶数,则小丽胜;否则,小芳胜.你认为对双方公平吗?请说明理由.
23. 如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.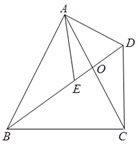 (1)、求证:∠ABD=∠ACD;(2)、若∠ACB=65°,求∠BDC的度数.24. 为庆祝“六一儿童节”,某幼儿园计划购买A、B两种玩具若干件,已知1件A种玩具的进价比1件B种玩具的进价贵2元,6件A种玩具的进价与7件B种玩具的进价和为350元.
(1)、求证:∠ABD=∠ACD;(2)、若∠ACB=65°,求∠BDC的度数.24. 为庆祝“六一儿童节”,某幼儿园计划购买A、B两种玩具若干件,已知1件A种玩具的进价比1件B种玩具的进价贵2元,6件A种玩具的进价与7件B种玩具的进价和为350元.
(1)、每件A种、B种玩具的进价分别是多少元?(2)、若该幼儿园计划购买这两种玩具共240件,且总费用不超过6600元,那么B种玩具最少可以买多少件?
25. 常州天宁宝塔是世界第一高佛塔.某校数学兴趣小组要测量宝塔的高度.如图,他们在点A处测得宝塔的最高点C的仰角为 ,再往宝塔方向前进65米至点B处,测得最高点C的仰角为 .请你根据这个兴趣小组测得的数据,计算宝塔的高度CD(参考数据: , ,结果精确到0.01米).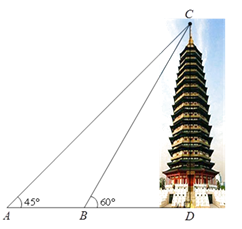 26. 观察下表:
26. 观察下表:
我们把某一格中所有字母相加得到的多项式称为特征多项式,例如:第1格的“特征多项式”为x+4y.
回答下列问题:
(1)、第4格的“特征多项式”为 , 第n格的“特征多项式”为;(2)、若第1格的“特征多项式”的值为2,第2格的“特征多项式”的值为-6.① 求x,y的值;
② 在①的条件下,第n格的“特征多项式的值”随着n的变化而变化,求“特征多项式的值”的最大值及此时n值.
27. 如图,正方形ABCD的边长为36 cm,点O以6 cm/s的速度从点B沿射线BC方向运动,射线AO交直线DC于点E.设点O运动的时间为t s. (1)、当t=9时,DE的长为cm;(2)、设DE=y,求y关于t的函数关系式;
(1)、当t=9时,DE的长为cm;(2)、设DE=y,求y关于t的函数关系式;
(3)、在线段BO上取点G,使得OC∶OG=4∶5.当以OC为半径的⊙O与直线AG相切时,求t的值.28. 如图1,在平面直角坐标系xOy中,直线l:y= 经过点A(4m,4),与y轴交于点B,抛物线 经过点A,交y轴于点C.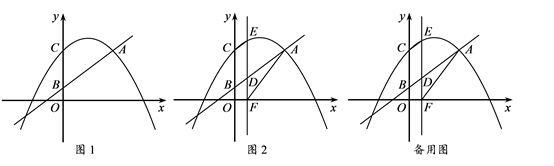 (1)、求直线l的解析式及抛物线的解析式;(2)、如图2,点D是直线l在第一象限内的一点,过点D作直线EF∥y轴,交抛物线于点E,交x轴于点F,连接AF,若∠CEF=∠CBA,求AF的长;(3)、在(2)的结论下,若点P是直线EF上一点,点Q是直线l上一点.当△PFA与△QPA全等时,直接写出点P和相应的点Q的坐标.
(1)、求直线l的解析式及抛物线的解析式;(2)、如图2,点D是直线l在第一象限内的一点,过点D作直线EF∥y轴,交抛物线于点E,交x轴于点F,连接AF,若∠CEF=∠CBA,求AF的长;(3)、在(2)的结论下,若点P是直线EF上一点,点Q是直线l上一点.当△PFA与△QPA全等时,直接写出点P和相应的点Q的坐标.