江苏省2018届数学中考押题卷

试卷更新日期：2018-07-18 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $3^{0} = 0$ B、 $- | - 3 | = - 3$ C、 $3^{- 1} = - 3$ D、 $\sqrt{9} = \pm 3$

查看试题解析
2. 分式 $\frac{2}{2 - x}$ 可变形为（）

A、 $\frac{2}{2 + x}$ B、 $- \frac{2}{2 + x}$ C、 $\frac{2}{x - 2}$ D、 $- \frac{2}{x - 2}$

查看试题解析
3. 抛物线 $y = - 3 x^{2} - x + 4$ 与坐标轴的交点个数是（）

A、3 B、2 C、1 D、0

查看试题解析
4. 如图，矩形ABCD，由四块小矩形拼成 $($ 四块小矩形放置是既不重叠，也没有空隙 $)$ ，其中 $② ③$ 两块矩形全等，如果要求出 $① ④$ 两块矩形的周长之和，则只要知道（）

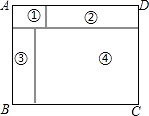A、矩形ABCD的周长 B、矩形 $②$ 的周长 C、AB的长 D、BC的长

查看试题解析

二、填空题

5. 若 $∠ A$ 为锐角，当 $tan A = \frac{\sqrt{3}}{3}$ 时， $cos A =$ ．

查看试题解析
6. 去年，中央财政安排资金8 200 000 000元，免除城市义务教育学生学杂费，支持进城务工人员随迁子女公平接受义务教育，这个数据用科学记数法可表示为元.

查看试题解析
7. “同位角相等”的逆命题是．

查看试题解析
8. 分解因式： $x^{3} - 2 x^{2} + x =$ ．

查看试题解析
9. 计算： $\frac{2 a}{a + 1}$ + $\frac{2}{a + 1}$ = ．

查看试题解析
10. 已知一元二次方程 $x^{2} - 3 x - 6 = 0$ 有两个实数根 $x_{1}$ 、 $x_{2}$ ，直线l经过点 $A (x_{1} + x_{2} ， 0)$ 、 $B (0 ， x_{1} \cdot x_{2})$ ，则直线l不经过第象限．

查看试题解析
11. 若一个圆锥的底面半径为2，母线长为6，则该圆锥侧面展开图的圆心角是°

查看试题解析
12. 如图，四边形ABCD是 $⊙ O$ 的内接四边形，点E在AB的延长线上，BF是 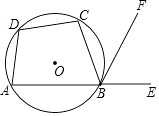$∠ C B E$ 的平分线， $∠ A D C = 100^{\circ}$ ，则 $∠ F B E =$ °

查看试题解析
13. 如图， $⊙ O$ 的直径AB与弦CD相交于点 $E ， A B = 5 ， A C = 3$ ，则 $tan ∠ A D C =$ ．

查看试题解析
14. 如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在函数 $y = x$ 的图象上，从左向右第3个正方形中的一个顶点A的坐标为 $(8 ， 4)$ ，阴影三角形部分的面积从左向右依次记为 $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ 、 $\dots$ 、 $S_{n}$ ，则 $S_{n}$ 的值为 $. ($ 用含n的代数式表示，n为正整数 $)$

查看试题解析

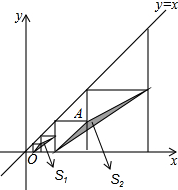
三、解答题

15. 请你先化简 $(\frac{a^{2}}{a + 2} - a + 2) \div \frac{4 a}{a^{2} - 4}$ ，再从 $- 2 ， 2 ， \sqrt{2}$ 中选择一个合适的数代入求值．

查看试题解析
16. 重庆市的重大惠民工程--公租房建设已陆续竣工，计划10年内解决低收入人群的住房问题，前6年，每年竣工投入使用的公租房面积 $y ($ 单位：百万平方米 $)$ ，与时间x的关系是 $y = - \frac{1}{6} x + 5 ， (x$ 单位：年， $1 \leq x \leq 6$ 且x为整数 $)$ ；后4年，每年竣工投入使用的公租房面积 $y ($ 单位：百万平方米 $)$ ，与时间x的关系是 $y = - \frac{1}{8} x + \frac{19}{4} (x$ 单位：年， $7 \leq x \leq 10$ 且x为整数 $) .$ 假设每年的公租房全部出租完 $.$ 另外，随着物价上涨等因素的影响，每年的租金也随之上调，预计，第x年投入使用的公租房的租金 $z ($ 单位：元 $/ m^{2})$ 与时间 $x ($ 单位：年， $1 \leq x \leq 10$ 且x为整数 $)$ 满足一次函数关系如下表：
$z ($ 元 $/ m^{2})$
50
52
54
56
58
$\dots$
$x ($ 年 $)$
1
2
3
4
5
$\dots$
$($ 参考数据： $\sqrt{315} \approx 17.7 ， \sqrt{319} \approx 17.8 ， \sqrt{321} \approx 17.9)$

(1)、求出z与x的函数关系式；

(2)、求政府在第几年投入的公租房收取的租金最多，最多为多少百万元；

(3)、若第6年竣工投入使用的公租房可解决20万人的住房问题，政府计划在第10年投入的公租房总面积不变的情况下，要让人均住房面积比第6年人均住房面积提高 $a %$ ，这样可解决住房的人数将比第6年减少 $1.35 a %$ ，求a的值．

查看试题解析
17. 计算： $\sqrt{8} + {(\frac{1}{2})}^{- 1} - 4 cos 45^{\circ} - {(\sqrt{3} - π)}^{0}$ ．

查看试题解析

18. 中国经济的快速发展让众多国家感受到了威胁，随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生，国家安全一再受到威胁，所谓“国家兴亡，匹夫有责”，某校积极开展国防知识教育，九年级甲、乙两班分别选5名同学参加“国防知识”比赛，其预赛成绩如图所示：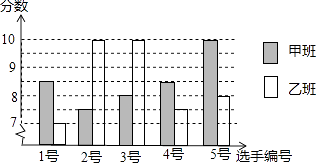

(1)、根据上图填写下表：

	平均数	中位数	众数	方差
甲班	$8.5$	$8.5$
乙班	$8.5$		10	$1.6$

(2)、根据上表数据，分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好．

查看试题解析

19. 已知：如图，▱ABCD中，O是CD的中点，连接AO并延长，交BC的延长线于点E．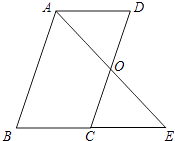

(1)、求证： $△ A O D$ ≌ $△ E O C$ ；

(2)、连接 $A C ， D E$ ，当 $∠ B =$ °和 $∠ A E B =$ °时，四边形ACED是正方形？请说明理由．

查看试题解析
20. 有两个构造完全相同（除所标数字外）的转盘A、B.

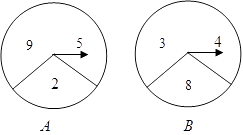(1)、单独转动A盘，指向奇数的概率是；

(2)、小红和小明做了一个游戏，游戏规定，转动两个转盘各一次，两次转动后指针指向的数字之和为奇数则小红获胜，数字之和为偶数则小明获胜，请用树状图或列表说明谁获胜的可能性大．

查看试题解析
21. 如图，甲、乙两渔船同时从港口O出发外出捕鱼，乙沿南偏东 $30^{\circ}$ 方向以每小时15海里的速度航行，甲沿南偏西 $75^{\circ}$ 方向以每小时 $15 \sqrt{2}$ 海里的速度航行，当航行1小时后，甲在A处发现自己的渔具掉在乙船上，于是迅速改变航向和速度，仍以匀速沿南偏东 $60^{\circ}$ 方向追赶乙船，正好在B处追上 $.$ 甲船追赶乙船的速度为多少海里 $/$ 小时？

查看试题解析
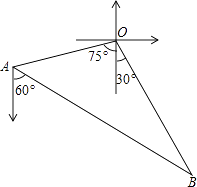22. 某商场经营某种品牌的玩具，购进时的单价是30元，根据市场调查：在一段时间内，销售单价是40元时，销售量是600件，而销售单价每涨1元，就会少售出10件玩具．

(1)、不妨设该种品牌玩具的销售单价为x元 $(x > 40)$ ，请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：
销售单价 $($ 元 $)$
x
销售量 $y ($ 件 $)$
销售玩具获得利润 $w ($ 元 $)$

(2)、在（1）问条件下，若商场获得了10000元销售利润，求该玩具销售单价x应定为多少元．

(3)、在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于44元，且商场要完成不少于540件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？

查看试题解析
23. 如图， $O A = 2$ ，以点A为圆心，1为半径画 $⊙ A$ 与OA的延长线交于点C，过点A画OA的垂线，垂线与 $⊙ A$ 的一个交点为B，连接BC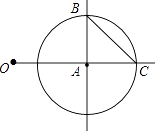

(1)、线段BC的长等于；

(2)、请在图中按下列要求逐一操作，并回答问题：
$①$ 以点为圆心，以线段的长为半径画弧，与射线BA交于点D，使线段OD的长等于 $\sqrt{6}$
$②$ 连OD，在OD上画出点P，使OP的长等于 $\frac{2 \sqrt{6}}{3}$ ，请写出画法，并说明理由．

查看试题解析
24. 如图，抛物线 $y = \frac{1}{4} x^{2} + b x + c$ 与x轴交于A、B两点，其中点 $B (2 ， 0)$ ，交y轴于点 $C (0 ， - \frac{5}{2}) .$ 直线 $y = m x + \frac{3}{2}$ 过点B与y轴交于点N，与抛物线的另一个交点是D，点P是直线BD下方的抛物线上一动点 $($ 不与点B、D重合 $)$ ，过点P作y轴的平行线，交直线BD于点E，过点D作 $D M ⊥ y$ 轴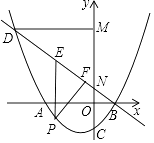于点M．

(1)、求抛物线 $y = \frac{1}{4} x^{2} + b x + c$ 的表达式及点D的坐标；

(2)、若四边形PEMN是平行四边形？请求出点P的坐标；

(3)、过点P作 $P F ⊥ B D$ 于点F，设 $△ P E F$ 的周长为C，点P的横坐标为a，求C与a的函数关系式，并求出C的最大值．

查看试题解析
25.

(1)、问题提出
如图1，点A为线段BC外一动点，且 $B C = a ， A B = b$ ，填空：当点A位于时，线段AC的长取得最大值，且最大值为 $($ 用含 $a ， b$ 的式子表示 $)$ ．

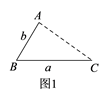(2)、问题探究
点A为线段BC外一动点，且 $B C = 6 ， A B = 3$ ，如图2所示，分别以 $A B ， A C$ 为边，作等边三角形ABD和等边三角形ACE，连接 $C D ， B E$ ，找出图中与BE相等的线段，请说明理由，并直接写出线段BE长的最大值．

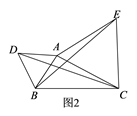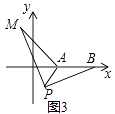
(3)、问题解决：
①如图3，在平面直角坐标系中，点A的坐标为 $(2 ， 0)$ ，点B的坐标为 $(5 ， 0)$ ，点P为线段AB外一动点，且 $P A = 2 ， P M = P B ， ∠ B P M = 90^{\circ}$ ，求线段AM长的最大值及此时点P的坐标．
$②$ 如图4，在四边形ABCD中， $A B = A D ， ∠ B A D = 60^{\circ} ， B C = 4 \sqrt{2}$ ，若对角线 $B D ⊥ C D$ 于点D，请直接写出对角线AC的最大值．

查看试题解析

$z ($ 元 $/ m^{2})$	50	52	54	56	58	$\dots$
$x ($ 年 $)$	1	2	3	4	5	$\dots$

销售单价 $($ 元 $)$	x
销售量 $y ($ 件 $)$
销售玩具获得利润 $w ($ 元 $)$