新人教版初中数学八年级下册 第十八章平行四边形 18.2特殊的平行四边形 18.2.3正方形 同步测试
试卷更新日期：2017-02-06 类型：同步测试
一、单选题
-
1. 下列性质中，正方形具有而矩形不一定具有的性质是（ ）A、对角线互相垂直 B、对角线互相平分 C、对角线相等 D、四个角都是直角2. 下列说法错误的是（ ）.A、有一个角为直角的菱形是正方形 B、有一组邻边相等的矩形是正方形 C、对角线相等的菱形是正方形 D、对角线相等且互相垂直的四边形是正方形3.
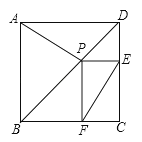
如图所示，在正方形ABCD中，AB=1，点P是对角线AC上的一点，分别以AP，PC为对角线作正方形，则两个小正方形的周长的和是（ ）
A、2 B、4 C、6 D、84. 若正方形的对角线长为2 cm，则这个正方形的面积为（ ）A、4cm2 B、2cm2 C、cm2 D、2cm25.如图，在正方形ABCD中，AB=4，P是线段AD上的动点，PE⊥AC于点E，PF⊥BD于点F，则PE+PF的值为（ ）
A、2 B、4 C、4 D、26. 若一个正方形的面积为8，则这个正方形的边长为（ ）A、4 B、2 C、 D、87. 正方形具有而菱形不一定具有的特征有（ ）A、对角线互相垂直平分 B、内角和为360° C、对角线相等 D、对角线平分内角8.已知在正方形ABCD中，对角线AC与BD相交于点O，OE∥AB交BC于点E，若AD=8cm，则OE的长为（ ）
A、3cm B、4cm C、6cm D、8cm9.如图，正方形ABCD中，AE=AB，直线DE交BC于点F，则∠BEF=（ ）
A、35° B、45° C、55° D、60°10.如图，边长分别为4和8的两个正方形ABCD和CEFG并排放在一起，连接BD并延长交BG于点T，交FG于点P，则ET的值为（ ）
A、2 B、3 C、4 D、611. 以面积为9cm2的正方形的对角线为边长的正方形面积为（ ）A、18cm2 B、20cm2 C、24cm2 D、28cm212. 若正方形的面积是4cm2 ， 则它的对角线长是（ ）A、4cm B、cm C、8cm D、2cm13.如图，下列四组条件中，能判定▱ABCD是正方形的有（ ）
①AB=BC，∠A=90°；②AC⊥BD，AC=BD；③OA=OD，BC=CD；④∠BOC=90°，∠ABD=∠DCA．
A、1个 B、2个 C、3个 D、4个14. 在正方形ABCD的边AB、BC、CD、DA上分别任意取点E、F、G、H ， 这样得到的四边形EFGH中，是正方形的有（ ）.A、1个 B、2个 C、4个 D、无穷多个15. 直角梯形ABCD中，∠A=∠D=90°，DC＜AB，AB=AD=12，E是边AD上的一点，恰好使CE=10，并且∠CBE=45°，则AE的长是（ ）A、2或8 B、4或6 C、5 D、3或7二、填空题
-
16.
如图，在四边形ABCD中，AB＝BC＝CD＝DA ， 对角线AC与BD相交于点O ， 若不增加任何字母与辅助线，要使四边形ABCD是正方形，则还需增加一个条件是
17.如图，在Rt△ABC中，∠C＝90°，DE垂直平分AC ， DF⊥BC ， 当△ABC满足条件时，四边形DECF是正方形．（要求：①不再添加任何辅助线，②只需填一个符合要求的条件）
18.如图，边长分别为3和5的两个正方形ABCD和CEFG并排放在一起，连结BD并延长交EG于点T，交FG于点P，则ET的长为
19.如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是 ．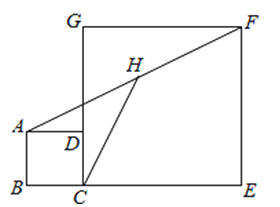
20.如图，正方形ABCD中，AB=1，点P是对角线AC上的一点，分别以AP、PC为对角线作正方形，则两个小正方形的周长的和是 ．
三、解答题
-
21.
如图，在正方形ABCD中，点E在对角线AC上，点F在边BC上，连接BE、DF，DF交对角线AC于点G，且DE=DG．
（1）求证：AE=CG；
（2）试判断BE和DF的位置关系，并说明理由．
22.如图，在正方形ABCD中，点E在对角线AC上，点F在边BC上，联结BE、DF，DF交对角线AC于点G，且DE=DG；
（1）求证：AE=CG；
（2）求证：BE∥DF．
23.如图，点B、C、E是同一直线上的三点，四边形ABCD与四边形CEFG都是正方形，连接BG、DE．
（1）求证：BG=DE；
（2）已知小正方形CEFG的边长为1cm，连接CF，如果将正方形CEFG绕点C逆时针旋转，当A、E两点之间的距离最小时，求线段CF所扫过的面积．
