2016-2017学年北京市密云二中高一上学期期中数学试卷
试卷更新日期:2017-02-06 类型:期中考试
一、选择题
-
1. 设集合A={1,2,4,6},B={2,3,5},则韦恩图中阴影部分表示的集合( )
 A、{2} B、{3,5} C、{1,4,6} D、{3,5,7,8}2. 为了得到函数y=2x﹣3﹣1的图象,只需把函数y=2x上所有点( )A、向右平移3个单位长度,再向下平移1个单位长度 B、向左平移3个单位长度,再向下平移1个单位长度 C、向右平移3个单位长度,再向上平移1个单位长度 D、向左平移3个单位长度,再向上平移1个单位长度3. 若0<m<n,则下列结论正确的是( )A、log m>log n B、log2m>log2n C、( )m<( )n D、2m>2n4. 设f(x)=x2+bx+c且f(0)=f(2),则( )A、f(﹣2)<f(0)<f( ) B、f( )<f(0)<f(﹣2) C、f( )<f(﹣2)<f(0) D、f(0)<f( )<f(﹣2)5. 函数y= 的图象大致是( )A、
A、{2} B、{3,5} C、{1,4,6} D、{3,5,7,8}2. 为了得到函数y=2x﹣3﹣1的图象,只需把函数y=2x上所有点( )A、向右平移3个单位长度,再向下平移1个单位长度 B、向左平移3个单位长度,再向下平移1个单位长度 C、向右平移3个单位长度,再向上平移1个单位长度 D、向左平移3个单位长度,再向上平移1个单位长度3. 若0<m<n,则下列结论正确的是( )A、log m>log n B、log2m>log2n C、( )m<( )n D、2m>2n4. 设f(x)=x2+bx+c且f(0)=f(2),则( )A、f(﹣2)<f(0)<f( ) B、f( )<f(0)<f(﹣2) C、f( )<f(﹣2)<f(0) D、f(0)<f( )<f(﹣2)5. 函数y= 的图象大致是( )A、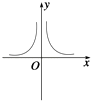 B、
B、 C、
C、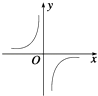 D、
D、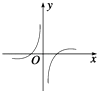 6. 函数y= 单调递减区间是( )A、(﹣∞, ) B、( ,+∞) C、(﹣∞,﹣1) D、(6,+∞)7. 设定义域为R的函数f(x)= ,则关于x的函数y=f(x)﹣1的零点的个数为( )A、1 B、2 C、3 D、48. 若直角坐标平面内的两点P、Q满足条件:
6. 函数y= 单调递减区间是( )A、(﹣∞, ) B、( ,+∞) C、(﹣∞,﹣1) D、(6,+∞)7. 设定义域为R的函数f(x)= ,则关于x的函数y=f(x)﹣1的零点的个数为( )A、1 B、2 C、3 D、48. 若直角坐标平面内的两点P、Q满足条件:①P、Q都在函数y=f(x)的图象上;
②P、Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”(点对[P,Q]与[Q,P]看作同一对“友好点对”),
已知函数f(x)= ,则此函数的“友好点对”有( )
A、0对 B、1对 C、2对 D、3对二、填空题
-
9. 若点(2, )在幂函数y=f(x)的图象上,则f(8)= .10. 函数f(x)= +lg(x+1)的定义域是.11. 函数 的零点个数是个.12.
设奇函数f(x)的定义域为[﹣5,5],若当x∈[0,5]时,f(x)的图象如图,则不等式f(x)<0的解集是
 13. 为了保证信息安全传输必须使用加密方式,有一种方式其加密、解密原理如下:
13. 为了保证信息安全传输必须使用加密方式,有一种方式其加密、解密原理如下:
已知加密为y=ax﹣2(x为明文、y为密文),如果明文“3”通过加密后得到密文为“6”,
再发送,接受方通过解密得到明文“3”,若接受方接到密文为“14”,则原发的明文是
14. 已知f (x)、g(x)都是定义在R上的函数,如果存在实数m、n使得h (x)=m f(x)+ng(x),那么称h (x)为f (x)、g(x)在R上生成的函数.设f (x)=x2+x、g(x)=x+2,若h (x)为f (x)、g(x)在R上生成的一个偶函数,且h(1)=3,则函数h(﹣1)=h (x)= .
三、解答题
-
15. 已知函数y= +lg(2﹣x)的定义域是集合M,集合N={x|x(x﹣3)<0}(1)、求M∪N;(2)、求(∁RM)∩N.16. 已知集合S={x|x2﹣3x﹣10<0},P={ x|a+1<x<2a+15},
(Ⅰ)求集合S;
(Ⅱ)若S⊆P,求实数a的取值范围.
17. 已知函数f(x)=2x , |(x≥0),图象如图所示.函数g(x)=﹣x2﹣2x+a,(x<0),其图象经过点A(﹣1,2). (1)、求实数a的值,并在所给直角坐标系xOy内做出函数g(x)的图象;(2)、设h(x)= ,根据h(x)的图象写出其单调区间.18. 已知0<a<1,函数f(x)=loga(ax﹣1)
(1)、求实数a的值,并在所给直角坐标系xOy内做出函数g(x)的图象;(2)、设h(x)= ,根据h(x)的图象写出其单调区间.18. 已知0<a<1,函数f(x)=loga(ax﹣1)(I)求函数f(x)的定义域;
(Ⅱ)判断f(x)的单调性;
(Ⅲ)若m满足f(1﹣m)≥f(1﹣m2),求m的范围.
19. 某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系如图一的一条折线表示;西红柿的种植成本与上市时间的关系如图二的抛物线段表示. (1)、写出图一表示的市场售价与时间的函数关系式p=f(t);写出图二表示的种植成本与时间的函数关系式Q=g(t);(2)、认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价各种植成本的单位:元/102㎏,时间单位:天)20. 对于定义域为D的函数y=f(x),若同时满足下列条件:
(1)、写出图一表示的市场售价与时间的函数关系式p=f(t);写出图二表示的种植成本与时间的函数关系式Q=g(t);(2)、认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价各种植成本的单位:元/102㎏,时间单位:天)20. 对于定义域为D的函数y=f(x),若同时满足下列条件:①f(x)在D内单调递增或单调递减;
②存在区间[a,b]⊆D,使f(x)在[a,b]上的值域为[a,b];那么把y=f(x)(x∈D)叫闭函数.
(1)、求闭函数y=﹣x3符合条件②的区间[a,b](2)、判断函数f(x)= 是否为闭函数?并说明理由;(3)、若y=k+ 是闭函数,求实数k的范围.