新人教版初中数学八年级下册 第十八章平行四边形 18.1.1平行四边形的性质 同步训练
试卷更新日期：2017-02-06 类型：同步测试
一、单选题
-
1.
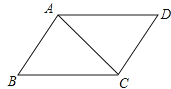
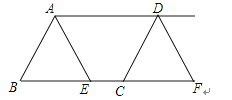
如图，在平行四边形ABCD和平行四边形AECF的顶点，D，E，F，B在一条直线上，则下列等式成立的是（ ）
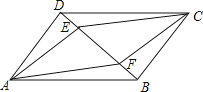A、AE=CE B、CE=CF C、DE=BF D、DE=EF=BF2.如图，在▱ABCD中，AC平分∠DAB，AB = 3，则▱ABCD的周长为（ ）
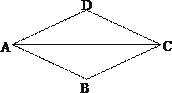A、6 B、9 C、12 D、153.如图，在▱ABCD中，对角线AC，BD相交于点0，OA=2，若要使▱ABCD为矩形，则OB的长应该为（ ） ．
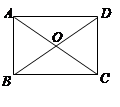A、4 B、3 C、2 D、14.如图，在平面直角坐标系中，以O（0，0）、A（1，-1）、B（2，0）为顶点，构造平行四边形，下列各点中不能作为平行四边形第四个顶点坐标的是
（ ）
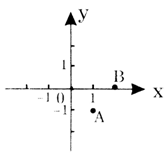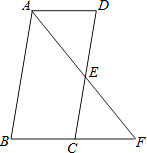
A、（3，-1） B、（-1，-1） C、（1，1） D、（-2，-1）5.如图，在梯形ABCD中，AD∥BC，两对角线交于点O，则图中面积相等的三角形有（ ）．
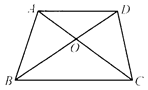A、4对 B、3对 C、2对 D、1对6.把直线a沿箭头方向平移1.5cm得直线b，这两条直线之间的距离是（ ）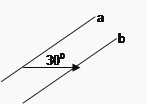
A、1.5cm B、3cm C、0.75cm D、cm7.如图，▱ABCD的周长是28 cm，△ABC的周长是22 cm，则AC的长为（ ）
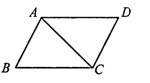A、6 cm B、12 cm C、4 cm D、8 cm8.如图所示，在□ABCD中，对角线AC ， BD交于点O ， 图中全等三角形有（ ）.
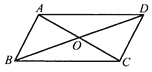A、5对 B、4对 C、3对 D、2对9.如图所示，在平行四边形ABCD中，∠ABE=∠AEB，AE∥DF，DC是∠ADF的角平分线．下列说法正确的是（ ）
①BE=CF ②AE是∠DAB的角平分线 ③∠DAE+∠DCF=120°．
A、① B、①② C、①②③ D、都不正确10.如图，在▱ABCD中，下列说法一定正确的是（ ）
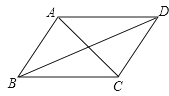A、AB⊥BC B、AC⊥BD C、AB=CD D、AB=BC11.如图，在平行四边形ABCD中，过点C的直线CE⊥AB，垂足为E，若∠EAD=54°，则∠BCE的度数为（ ）
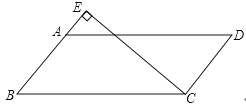A、54° B、36° C、46° D、126°12. ▱ABCD中，∠A：∠B：∠C：∠D的值可以等于（ ）A、1：2：3：4 B、3：4：4：3 C、3：3：4：4 D、3：4：3：413.如图，在▱ABCD中，O是对角线AC，BD的交点，下列结论错误的是（ ）
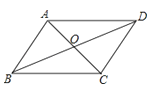A、AB∥CD B、AB=CD C、AC=BD D、OA=OC14. 如图，在▱ABCD中，AC与BD交于点O，点E是BC边的中点，OE=1，则AB的长是（ ）
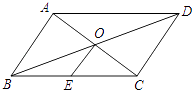A、1 B、2 C、 D、415. 在平面直角坐标系中，平行四边形ABCD的顶点A，B，D的坐标分别是（0，0），（5，0），（2，3），则顶点C的坐标是（ ）
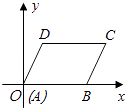A、（3，7） B、（5，3） C、（7，3） D、（8，2）二、填空题
-
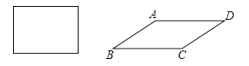
16.
将四根木条钉成的长方形木框变形为平行四边形ABCD的形状，并使其面积为长方形面积的一半（木条宽度忽略不计），则这个平行四边形的最小内角为度．
17.如图，在▱ABCD中，AB= ， AD=4，将▱ABCD沿AE翻折后，点B恰好与点C重合，则折痕AE的长为 .
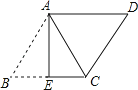18.如图，平行四边形ABCD的对角线AC、BD相交于点O，BC=9，AC=8，BD=14，则△AOD的周长为 ．
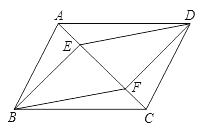
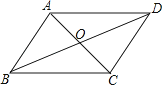19.如图，在▱ABCD 中，EF经过对角线的交点O，交AB于点E，交CD于点F．若AB=5，AD=4，OF=1.8，那么四边形BCFE的周长为 ．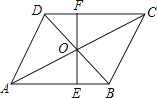
20.如图，P为平行四边形ABCD边AD上一点，E、F分别为PB、PC的中点，若△PEF的面积为3，那么△PDC与△PAB的面积和等于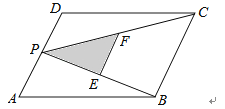
三、解答题
-
21.
如图，平行四边形ABCD中，AE⊥BC，CF⊥AD，垂足分别是E、F．求证：△ABE≌△CDF．
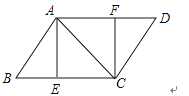22.已知ABCD是平行四边形，用尺规分别作出△BAC与△DAC共公边AC上的高BE、DF．求证：BE=DF．
