新人教版初中数学八年级下册 第十七章勾股定理 17.1勾股定理 同步测试
试卷更新日期：2017-02-06 类型：同步测试
一、单选题
-
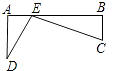
1. 已知三角形两边长为2和6，要使这个三角形为直角三角形，则第三边的长为（ ）A、 B、2 C、4或2 D、以上都不对2. 三角形的三边长分别为6、8、10，它的最短边上的高为( )A、6 B、4.5 C、2.4 D、83.
一块木板如图所示，已知AB＝4，BC＝3，DC＝12，AD＝13，∠B＝90°，木板的面积为（）
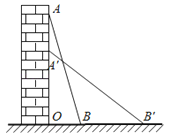
A、60 B、30 C、24 D、124. 一座建筑物发生了火灾，消防车到达现场后，发现最多只能靠近建筑物底端5米，消防车的云梯最大升长为13米，则云梯可以达该建筑物的最大高度是（ ）
A、12米 B、13米 C、14米 D、15米5. 已知直角三角形两边的长为3和4，则此三角形的周长为（ ）．A、12 B、7＋ C、12或7＋ D、以上都不对6.如图所示，一场暴雨过后，垂直于地面的一棵树在距地面1米处折断，树尖B 恰好碰到地面，经测量AB=2米，则树高为（ ）
A、米 B、米 C、(米 D、3 米7.正方形的网格中，每个小正方形的边长为1，则网格中三角形ABC中，边长是无理数的边数是（ ）
A、0 B、1 C、2 D、38.如图，由4个相同的直角三角形与中间的小正方形拼成一个大正方形，若大正方形面积是9，小正方形面积是1，直角三角形较长直角边为a，较短直角边为b，则ab的值是（ ）
A、4 B、6 C、8 D、109.如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3 ． 若S1+S2+S3=15，则S2的值是（ ）
A、3 B、 C、5 D、10.图1为一个长方体，AD=AB=10，AE=6，M，N为所在棱的中点，图2为图1的表面展开图，则图2中MN的长度为（ ）
A、11 B、10 C、10 D、811.图1是边长为1的六个小正方形组成的图形，它可以围成图2的正方体，则图1中正方形顶点A、B在围成的正方体中的距离是（ ）
A、0 B、1 C、 D、12.如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S1、S2 ， 则S1+S2的值为（ ）
A、16 B、17 C、18 D、1913.如图所示：某商场有一段楼梯，高BC=6m，斜边AC是10米，如果在楼梯上铺上地毯，那么需要地毯的长度是（ ）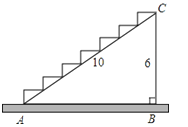
A、8m B、10m C、14m D、24m14.如图，直角三角形三边上的半圆面积从小到大依次记为S1、S2、S3 ， 则S1、S2、S3之间的关系是（ ）
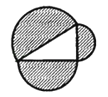A、Sl+S2＞S3 B、Sl+S2＜S3 C、S1+S2=S3 D、S12+S22=S3215.一个圆桶底面直径为24cm，高32cm，则桶内所能容下的最长木棒为（ ）
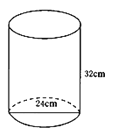A、20cm B、50cm C、40cm D、45cm二、填空题
-
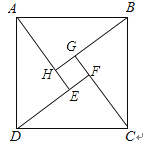
16.
如图是“赵爽弦图”，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形．如果AB=10，EF=2，那么AH等于 .
17.如图，将一根长24cm的筷子，置于底面直径为5cm，高为12cm的圆柱形茶杯中，设筷子露在杯子外面的长为acm（茶杯装满水），则a的取值范围是 ．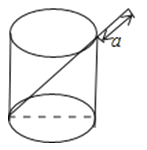
18. 放学以后，萍萍和晓晓从学校分手，分别沿东南方向和西南方向回家，若萍萍和晓晓行走的速度都是40米/分，萍萍用15分钟到家，晓晓用20分钟到家，萍萍家和晓晓家的距离为 米．19. 要在一个长方体中放入一细直木条，现知长方体的长为2，宽为 ， 高为 ， 则放入木盒的细木条最大长度为 ．
20.学校有一块长方形的花圃如右图所示，有少数的同学为了避开拐角走“捷径”，在花圃内走出了一条“路”，他们仅仅少走了步（假设1米=2步），却踩伤了花草，所谓“花草无辜，踩之何忍”！
三、综合题
-
21.
如图，正方形网格中的△ABC，若小方格边长为1，
(1)、判断△ABC的形状，说明理由．(2)、求A到BC的距离．四、解答题
-
22.
如图，甲、乙两艘轮船同时从港口O出发，甲轮船以20海里/时的速度向南偏东45°方向航行，乙轮船向南偏西45°方向航行．已知它们离开港口O两小时后，两艘轮船相距50海里，求乙轮船平均每小时航行多少海里？
-
