辽宁省沈阳市郊联体2017-2018学年高一下学期文数期中考试试卷

试卷更新日期：2018-07-17 类型：期中考试

进入出卷网下载

一、单选题

1. 已知 $sin α > 0, cos α < 0$ ，则 $α$ 的终边落在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 已知向量 $\overset{⇀}{a} = (1, 2), \overset{⇀}{b} = (- 2, 1)$ ，则 $\overset{⇀}{a} + 2 \overset{⇀}{b} =$ （）

A、 $(0, 5)$ B、 $(5, - 1)$ C、 $(- 1, 3)$ D、 $(- 3, 4)$

查看试题解析
3. 已知 $α ， β$ 为锐角，且 $cos α = \frac{1}{\sqrt{10}} ， cos β = \frac{1}{\sqrt{5}}$ ，则 $α + β$ 的值是（）

A、 $\frac{2}{3} π$ B、 $\frac{3}{4} π$ C、 $\frac{π}{4}$ D、 $\frac{π}{3}$

查看试题解析
4. 已知 $\overset{⇀}{a} ， \overset{⇀}{b}$ 均为单位向量，它们的夹角为 $60^{0}$ ，那么 $| \overset{⇀}{a} + 3 \overset{⇀}{b} | =$ （）

A、 $\sqrt{7}$ B、 $\sqrt{10}$ C、 $\sqrt{13}$ D、4

查看试题解析
5. 函数 $f (x) = sin 2 x - 4 {sin}^{3} x cos x (x \in R)$ 的最小正周期为（）

A、 $\frac{π}{2}$ B、 $\frac{π}{4}$ C、 $\frac{π}{8}$ D、 $π$

查看试题解析
6. $tan 36 ° + tan 84 ° - \sqrt{3} tan 36 ° tan 84 ° =$ （）

A、 $- \sqrt{3}$ B、 $\sqrt{3}$ C、 $- \frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
7. 已知 $\frac{cos α}{1 + sin α} = \sqrt{3}$ ，则 $\frac{cos α}{sin α - 1}$ 的值为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $- \frac{\sqrt{3}}{3}$ C、 $\sqrt{3}$ D、 $- \sqrt{3}$

查看试题解析
8. 为得到函数y=sin $(x + \frac{π}{3})$ 的图象，可将函数y=cosx的图象向右平移m（m＞0）个单位长度，则m的最小值是（）

A、 $\frac{11}{6} π$ B、 $\frac{5}{6} π$ C、 $\frac{π}{3}$ D、 $\frac{π}{6}$

查看试题解析
9. 已知 $tan (π - α) = 2$ ，则 $\frac{sin α - cos α}{sin α + cos α}$ 的值为（）

A、3 B、2 C、 $- 3$ D、 $\frac{1}{3}$

查看试题解析
10. 若点 $P (sin α - cos α ， tan α)$ 在第一象限，则在 $[0 ， 2 π)$ 内 $α$ 的取值范围是（）

A、 $(\frac{π}{4} ， \frac{π}{2}) \cup^{} (π ， \frac{5 π}{4})$ B、 $(\frac{π}{2} ， \frac{3 π}{4}) \cup^{} (\frac{5 π}{4} ， \frac{3 π}{2})$ C、 $(\frac{π}{2} ， \frac{3 π}{4}) \cup^{} (\frac{3 π}{4} ， π)$

查看试题解析
11. 函数 $y = \frac{sin 2 x}{1 - cos x}$ 的部分图像大致为（）

A、 B、 C、 D、

查看试题解析
12. 已知 $A B$ 是圆 $C ： {(x - 1)}^{2} + y^{2} = 1$ 的直径，点 $P$ 为直线 $x - y + 1 = 0$ 上任意一点，则 $\overset{⇀}{P A} \cdot \overset{⇀}{P B}$ 的最小值是（）

A、 $\sqrt{2} - 1$ B、 $\sqrt{2}$ C、0 D、1

查看试题解析

二、填空题

13. 已知非零向量 $\overset{⇀}{a} ， \overset{⇀}{b}$ 满足 $| \overset{⇀}{a} + \overset{⇀}{b} | = | \overset{⇀}{a} - \overset{⇀}{b} |$ ，则 $〈 \overset{⇀}{a} ， \overset{⇀}{b} 〉 =$ ．

查看试题解析
14. 函数 $y = A sin (ω x + ϕ) (A > 0 ， | ϕ | < \frac{π}{2})$ 的部分图象如图，则函数解析式为.

查看试题解析
15. 若 $sin (x + \frac{π}{6}) = \frac{1}{4}$ ，则 $sin (\frac{5 π}{6} - x) {sin}^{2} (\frac{π}{3} - x) + cos (2 x + \frac{π}{3}) =$ ．

查看试题解析
16. 三角形 $A B C$ 是锐角三角形，若角 $θ$ 终边上一点 $P$ 的坐标为 $(sin A - cos B ， cos A - sin B)$ ，则 $\frac{sin θ}{| sin θ |} + \frac{cos θ}{| cos θ |} + \frac{tan θ}{| tan θ |}$ 的值是.

查看试题解析

三、解答题

17. 已知向量 $\overset{⇀}{O A} = (2 ， - 3)$ ， $\overset{⇀}{O B} = (- 5 ， 4)$ ， $\overset{⇀}{O C} = (1 - λ ， 3 λ + 2)$ .

(1)、若 $Δ A B C$ 为直角三角形，且 $∠ B$ 为直角，求实数 $λ$ 的值；

(2)、若点 $A ， B ， C$ 能构成三角形，求实数 $λ$ 应满足的条件.

查看试题解析
18. 已知 $α \in (\frac{π}{2} ， π) ， sin α + cos α = \frac{1}{5}$ .

(1)、求 $sin α - cos α$ 的值；

(2)、求 $sin (α + \frac{π}{3})$ 的值.

查看试题解析
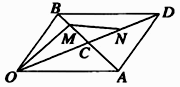
19. 如图所示，以向量 $\overset{⇀}{O A} = \overset{⇀}{a} ， \overset{⇀}{O B} = \overset{⇀}{b}$ 为边作平行四边形 $O A D B$ ，又 $\overset{⇀}{B M} = \frac{1}{3} \overset{⇀}{B C}$ ， $\overset{⇀}{C N} = \frac{1}{3} \overset{⇀}{C D}$ ，用 $\overset{⇀}{a} ， \overset{⇀}{b}$ 表示 $\overset{⇀}{O M} ， \overset{⇀}{O N} ， \overset{⇀}{M N}$ .

查看试题解析
20. 已知函数 $y = A sin (ω x + ϕ) (A > 0 ， ω > 0 ， | ϕ | < \frac{π}{2})$ 的图象过点 $P (\frac{π}{12} ， 0)$ ，且图象上与 $P$ 点最近的一个最高点坐标为 $(\frac{π}{3} ， 5)$ .

(1)、求函数的解析式；

(2)、若将此函数的图象向左平移 $\frac{π}{6}$ 个单位长度后，再向下平移2个单位长度得到 $g (x)$ 的图象，求 $g (x)$ 在 $x \in [- \frac{π}{6} ， \frac{π}{3}]$ 上的值域.

查看试题解析
21. 已知函数 $f (x) = {sin}^{2} ω x - \sqrt{3} sin ω x cos ω x + \frac{1}{2} (ω > 0)$ ， $y = f (x)$ 的图象与直线 $y = 2$ 相交，且两相邻交点之间的距离为 $π$ .

(1)、求 $f (x)$ 的解析式，并求 $f (x)$ 的单调区间；

(2)、已知函数 $g (x) = m cos (x + \frac{π}{3}) - m + 2$ ，若对任意 $x_{1} ， x_{2} \in [0 ， π]$ ，均有 $f (x_{1}) \geq g (x_{2})$ ，求 $m$ 的取值范围.

查看试题解析
22. 已知向量 $\overset{⇀}{a} = (cos \frac{3}{2} x ， sin \frac{3}{2} x) ， \overset{⇀}{b} = (cos \frac{x}{2} ， sin \frac{x}{2})$ 且 $x \in [0 ， \frac{π}{2}]$

(1)、求 $\overset{⇀}{a} \cdot \overset{⇀}{b}$ 及 $| \overset{⇀}{a} + \overset{⇀}{b} |$ ；

(2)、若 $f (x) = \overset{⇀}{a} \cdot \overset{⇀}{b} - 2 λ$ $| \overset{⇀}{a} + \overset{⇀}{b} |$ 的最小值是 $- \frac{3}{2}$ ，求实数 $λ$ 的值.

查看试题解析