四川省成都市青羊区2018届数学中考一模试卷
试卷更新日期:2018-07-17 类型:中考模拟
一、单选题
-
1. cos30°的值为( )A、 B、 C、 D、2.
如图,是由一个圆柱体和一个长方体组成的几何体.其主视图是( )
 A、
A、 B、
B、 C、
C、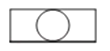 D、
D、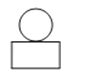 3. 下列说法正确的是( )A、对角线相等的四边形是矩形 B、有两边及一角对应相等的两个三角形全等 C、对角线互相垂直的矩形是正方形 D、平分弦的直径垂直于弦4. 某厂一月份生产产品50台,计划二、三月份共生产产品120台,设二、三月份平均每月增长率为x,根据题意,可列出方程为( )A、50(1+x)2=60 B、50(1+x)2=120 C、50+50(1+x)+50(1+x)2=120 D、50(1+x)+50(1+x)2=1205. 函数y= 自变量x的取值范围是( )A、x≥3 B、x≤3 C、x>3 D、x<36. 如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠OCB的度数为( )
3. 下列说法正确的是( )A、对角线相等的四边形是矩形 B、有两边及一角对应相等的两个三角形全等 C、对角线互相垂直的矩形是正方形 D、平分弦的直径垂直于弦4. 某厂一月份生产产品50台,计划二、三月份共生产产品120台,设二、三月份平均每月增长率为x,根据题意,可列出方程为( )A、50(1+x)2=60 B、50(1+x)2=120 C、50+50(1+x)+50(1+x)2=120 D、50(1+x)+50(1+x)2=1205. 函数y= 自变量x的取值范围是( )A、x≥3 B、x≤3 C、x>3 D、x<36. 如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠OCB的度数为( )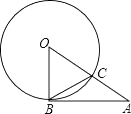 A、40° B、50° C、65° D、75°7. 对于抛物线y=(x﹣1)2+2的说法错误的是( )A、抛物线的开口向上 B、抛物线的顶点坐标是(1,2) C、抛物线与x轴无交点 D、当x<1时,y随x的增大而增大8. 如图,点A是反比例函数y= 的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为4,则k的值是( )
A、40° B、50° C、65° D、75°7. 对于抛物线y=(x﹣1)2+2的说法错误的是( )A、抛物线的开口向上 B、抛物线的顶点坐标是(1,2) C、抛物线与x轴无交点 D、当x<1时,y随x的增大而增大8. 如图,点A是反比例函数y= 的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为4,则k的值是( ) A、4 B、﹣4 C、8 D、﹣89. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
A、4 B、﹣4 C、8 D、﹣89. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:甲
乙
丙
丁
平均数(cm)
180
185
185
180
方差
3.6
3.6
7.4
8.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁10. 如图,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB:FG=2:3,则下列结论正确的是( )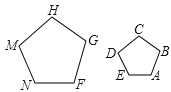 A、2DE=3MN B、3DE=2MN C、3∠A=2∠F D、2∠A=3∠F
A、2DE=3MN B、3DE=2MN C、3∠A=2∠F D、2∠A=3∠F二、填空题
-
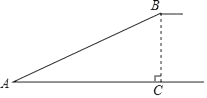
11. 一只不透明的袋子共装有3个小球,它们的标号分别为1,2,3,从中摸出1个小球,标号为“小于3”的概率为12. 如图,已知斜坡 AB 的坡度为 1:3.若坡长 AB=10m,则坡高 BC=m.
 13. 如图,在▱ABCD中,∠C=43°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为
13. 如图,在▱ABCD中,∠C=43°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为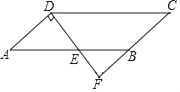 14. 如图,AB和DE是直立在地面上的两根立柱,AB=5米,某一时刻AB在阳光下的投影BC=3米,在测量AB的投影时,同时测量出DE在阳光下的投影长为6米,则DE的长为
14. 如图,AB和DE是直立在地面上的两根立柱,AB=5米,某一时刻AB在阳光下的投影BC=3米,在测量AB的投影时,同时测量出DE在阳光下的投影长为6米,则DE的长为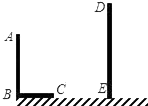 15. 已知关于x的一元二次方程x2﹣mx+2m﹣1=0的两根x1、x2满足x12+x22=14,则m=16. 如图,由点P(14,1),A(a,0),B(0,a)(0<a<14)确定的△PAB的面积为18,则a的值为
15. 已知关于x的一元二次方程x2﹣mx+2m﹣1=0的两根x1、x2满足x12+x22=14,则m=16. 如图,由点P(14,1),A(a,0),B(0,a)(0<a<14)确定的△PAB的面积为18,则a的值为 17. 如图,在直角坐标系中,⊙A的圆心的坐标为(﹣2,0),半径为2,点P为直线y=﹣ x+6上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是
17. 如图,在直角坐标系中,⊙A的圆心的坐标为(﹣2,0),半径为2,点P为直线y=﹣ x+6上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是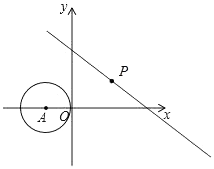 18. 如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI=
18. 如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI= 19. 如图,已知正方形ABCD的边长是⊙O半径的4倍,圆心O是正方形ABCD的中心,将纸片按图示方式折叠,使EA'恰好与⊙O相切于点A',则tan∠A'FE的值为
19. 如图,已知正方形ABCD的边长是⊙O半径的4倍,圆心O是正方形ABCD的中心,将纸片按图示方式折叠,使EA'恰好与⊙O相切于点A',则tan∠A'FE的值为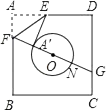
三、解答题
-
20.
(1)、计算:(﹣1)2017﹣( )﹣2•sin60°+|3﹣ |
(2)、解方程:2(x﹣2)2=x2﹣421. 如图,在Rt△ABC中,∠ACB=90°,D为AB中点,AE∥CD,CE∥AB.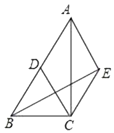 (1)、试判断四边形ADCE的形状,并证明你的结论.(2)、连接BE,若∠BAC=30°,CE=1,求BE的长.22. 据新浪网调查,在第十二届全国人大二中全会后,全国网民对政府工作报告关注度非常高,大家关注的热点话题分别有:消费、教育、环保、反腐及其它共五类,且关注五类热点问题的网民的人数所占百分比如图l所示,关注该五类热点问题网民的人数的不完整条形统计如图2,请根据图中信息解答下列问题.
(1)、试判断四边形ADCE的形状,并证明你的结论.(2)、连接BE,若∠BAC=30°,CE=1,求BE的长.22. 据新浪网调查,在第十二届全国人大二中全会后,全国网民对政府工作报告关注度非常高,大家关注的热点话题分别有:消费、教育、环保、反腐及其它共五类,且关注五类热点问题的网民的人数所占百分比如图l所示,关注该五类热点问题网民的人数的不完整条形统计如图2,请根据图中信息解答下列问题. (1)、求出图l中关注“反腐”类问题的网民所占百分比x的值,并将图2中的不完整的条形统计图补充完整;
(1)、求出图l中关注“反腐”类问题的网民所占百分比x的值,并将图2中的不完整的条形统计图补充完整;
(2)、为了深度了解成都网民对政府工作报告的想法,新浪网邀请成都市5名网民代表甲、乙、丙、丁、戊做客新浪访谈,且一次访谈只选2名代表.请你用列表法或画树状图的方法,求出一次所选代表恰好是丙和丁的概率.23. 如图,小明到青城山游玩,乘坐缆车,当登山缆车的吊箱经过点A到达点B时,它经过了200 m,缆车行驶的路线与水平夹角∠α=16°,当缆车继续由点B到达点D时,它又走过了200 m,缆车由点B到点D的行驶路线与水平夹角∠β=42°,求缆车从点A到点D垂直上升的距离.(结果保留整数)(参考数据:sin16°≈0.27,cos16°≈0.77,sin42°≈0.66,cos42°≈0.74)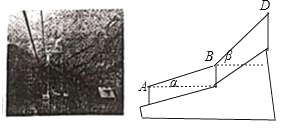 24. 如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,4),点A为MN的中点,反比例函数y= (x>0)的图象过点A.
24. 如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,4),点A为MN的中点,反比例函数y= (x>0)的图象过点A.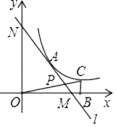 (1)、求直线l和反比例函数的解析式;(2)、在函数y= (k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.25. 如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆经过点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G,且D是 的中点.
(1)、求直线l和反比例函数的解析式;(2)、在函数y= (k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.25. 如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆经过点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G,且D是 的中点.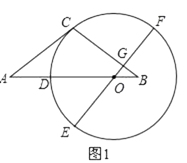 (1)、求证:AC是⊙O的切线;(2)、如图2,延长CB交⊙O于点H,连接HD交OE于点P,连接CF,求证:CF=DO+OP;
(1)、求证:AC是⊙O的切线;(2)、如图2,延长CB交⊙O于点H,连接HD交OE于点P,连接CF,求证:CF=DO+OP;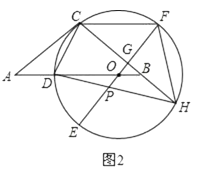 (3)、在(2)的条件下,连接CD,若tan∠HDC= ,CG=4,求OP的长.26. 某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
(3)、在(2)的条件下,连接CD,若tan∠HDC= ,CG=4,求OP的长.26. 某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:售价x(元/千克)
50
60
70
销售量y(千克)
100
80
60
(1)、求y与x之间的函数表达式;
(2)、设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?(3)、如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.27. 如图,已知一个三角形纸片ACB,其中∠ACB=90°,AC=8,BC=6,E、F分别是AC、AB边上的点,连接EF.(1)、如图1,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=4S△EDF , 求ED的长;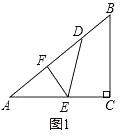 (2)、如图2,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
(2)、如图2,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.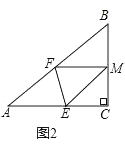
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)、如图3,若FE的延长线与BC的延长线交于点N,CN=2,CE= ,求 的值.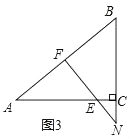 28. 如图,直线y=﹣ x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+ x+c经过B、C两点.
28. 如图,直线y=﹣ x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+ x+c经过B、C两点. (1)、求抛物线的解析式;
(1)、求抛物线的解析式;
(2)、如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标;
(3)、在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.