上海市长宁区2018届九年级数学中考一模试卷

试卷更新日期：2018-07-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 在Rt△ABC中，∠C=90°，∠A=α，AC=3，则AB的长可以表示为（）

A、 $\frac{3}{cos α}$ B、 $\frac{3}{sin α}$ C、3sinα D、3cosα

查看试题解析
2. 如图，在△ABC中，点D，E分别在边BA，CA的延长线上， $\frac{A B}{A D}$ =2，那么下列条件中能判断DE∥BC的是（）

A、 $\frac{A E}{E C} = \frac{1}{2}$ B、 $\frac{E C}{A C} = 2$ C、 $\frac{D E}{B C} = \frac{1}{2}$ D、 $\frac{A C}{A E} = 2$

查看试题解析
3. 将抛物线y=﹣（x+1）²+3向右平移2个单位后得到的新抛物线的表达式为（）

A、y=﹣（x+1）²+1 B、y=﹣（x﹣1）²+3 C、y=﹣（x+1）²+5 D、y=﹣（x+3）²+3

查看试题解析
4. 已知在直角坐标平面内，以点P（﹣2，3）为圆心，2为半径的圆P与x轴的位置关系是（）

A、相离 B、相切 C、相交 D、相离、相切、相交都有可能

查看试题解析
5. 已知 $\overset{⇀}{e}$ 是单位向量，且 $\overset{⇀}{a} = - 2 \overset{⇀}{e} ， \overset{⇀}{b} = 4 \overset{⇀}{e}$ ，那么下列说法错误的是（）

A、 $\overset{⇀}{a}$ ∥ $\overset{⇀}{b}$ B、| $\overset{⇀}{a}$ |=2 C、| $\overset{⇀}{b}$ |=﹣2| $\overset{⇀}{a}$ | D、 $\overset{⇀}{a}$ =﹣ $\frac{1}{2} \overset{⇀}{b}$

查看试题解析
6. 如图，在四边形ABCD中，对角线AC与BD相交于点O，AC平分∠DAB，且∠DAC=∠DBC，那么下列结论不一定正确的是（）

A、△AOD∽△BOC B、△AOB∽△DOC C、CD=BC D、BC•CD=AC•OA

查看试题解析

二、填空题

7. 若线段a、b满足 $\frac{a}{b} = \frac{1}{2}$ ，则 $\frac{a+b}{b}$ 的值为．

查看试题解析
8. 正六边形的中心角等于度．

查看试题解析
9. 若抛物线y=（a﹣2）x²的开口向上，则a的取值范围是．

查看试题解析
10. 抛物线y=x²﹣4x+3的顶点坐标为．

查看试题解析
11. 已知△ABC与△DEF相似，且△ABC与△DEF的相似比为2：3，若△DEF 的面积为36，则△ABC的面积等于．

查看试题解析
12. 已知线段AB=4，点P是线段AB的黄金分割点，且AP＜BP，那么AP的长为．

查看试题解析
13. 若某斜面的坡度为1： $\sqrt{3}$ ，则该坡面的坡角为度．

查看试题解析
14. 已知点A（﹣2，m）、B（2，n）都在抛物线y=x²+2x﹣t上，则m与n的大小关系是mn．（填“＞”、“＜”或“=”）

查看试题解析
15. 如图，在Rt△ABC中，∠BAC=90°，点G是重心，联结AG，过点G作DG∥BC，DGAB于D，若AB=6，BC=9，则△ADG的周长等于．

查看试题解析
16. 已知⊙O₁的半径为4，⊙O₂的半径为R，若⊙O₁与⊙O₂相切，且O₁O₂=10，则R的值为．

查看试题解析
17. 如果一个四边形的某个顶点到其他三个顶点的距离相等，我们把这个四边形叫做等距四边形，这个顶点叫做这个四边形的等距点．如图，已知梯形ABCD是等距四边形，AB∥CD，点B是等距点．若BC=10，cosA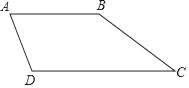= $\frac{\sqrt{10}}{10}$ ，则CD的长等于．

查看试题解析
18. 如图，在边长为2的菱形ABCD中，∠D=60°，点E、F分别在边AB、BC上．将△BEF沿着直线EF翻折，点B恰好与边AD的中点G重合，则BE的长等于

查看试题解析

三、解答题

19. 计算： $\frac{cot 45 °}{4 {sin}^{2} 45 ° - tan 60 °} - cos 30 °$ ．

查看试题解析
20. 如图，在△ABC中，点D在边AB上，DE∥BC，DF∥AC，DE、DF分别交边AC、BC于点E、F，且 $\frac{A E}{E C} = \frac{3}{2}$ ．

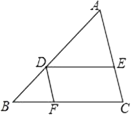(1)、求 $\frac{B F}{F C}$ 的值；

(2)、联结EF，设 $\overset{⇀}{B C}$ = $\overset{⇀}{a}$ ， $\overset{⇀}{A C}$ = $\overset{⇀}{b}$ ，用含 $\overset{⇀}{a}$ 、 $\overset{⇀}{b}$ 的式子表示 $\overset{⇀}{E F}$ ．

查看试题解析
21. 如图，点C在⊙O上，联结CO并延长交弦AB于点D， $\vec{A C} = \vec{B C}$ ，联结AC、OB，若CD=40，AC=20 $\sqrt{5}$ ．

(1)、求弦AB的长；

(2)、求sin∠ABO的值．

查看试题解析
22. 如图，一栋居民楼AB的高为16米，远处有一栋商务楼CD，小明在居民楼的楼底A处测得商务楼顶D处的仰角为60°，又在商务楼的楼顶D处测得居民楼的楼顶B处的俯角为45°．其中A、C两点分别位于B、D两点的正下方，且A、C两点在同一水平线上，求商务楼CD的高度．
（参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732．结果精确到0.1米）

查看试题解析
23. 如图，在△ABC中，点D在边BC上，联结AD，∠ADB=∠CDE，DE交边AC于点E，DE交BA延长线于点F，且AD²=DE•DF．

(1)、求证：△BFD∽△CAD；

(2)、求证：BF•DE=AB•AD．

查看试题解析
24. 在直角坐标平面内，直线y= $\frac{1}{2}$ x+2分别与x轴、y轴交于点A、C．抛物线y=﹣ $\frac{1}{2} x^{2}$ +bx+c经过点A与点C，且与x轴的另一个交点为点B．点D在该抛物线上，且位于直线AC的上方．

(1)、求上述抛物线的表达式；

(2)、联结BC、BD，且BD交AC于点E，如果△ABE的面积与△ABC的面积之比为4：5，求∠DBA的余切值；

(3)、过点D作DF⊥AC，垂足为点F，联结CD．若△CFD与△AOC相似，求点D的坐标．

查看试题解析
25. 已知在矩形ABCD中，AB=2，AD=4．P是对角线BD上的一个动点（点P不与点B、D重合），过点P作PF⊥BD，交射线BC于点F．联结AP，画∠FPE=∠BAP，PE交BF于点E．设PD=x，EF=y．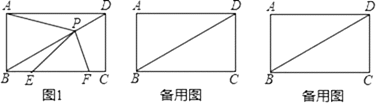

(1)、当点A、P、F在一条直线上时，求△ABF的面积；

(2)、如图1，当点F在边BC上时，求y关于x的函数解析式，并写出函数定义域；

(3)、联结PC，若∠FPC=∠BPE，请直接写出PD的长．

查看试题解析