江苏省无锡市惠山区2016-2017学年七年级下学期数学期末考试试卷
试卷更新日期:2018-07-17 类型:期末考试
一、单选题
-
1. 下列运算中,正确的是( )A、 B、 C、 D、2. 如果 ,下列各式中正确的是( )A、 B、 C、 D、3. 不等式组 的解集在数轴上可以表示为( )。A、
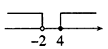 B、
B、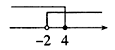 C、
C、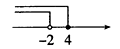 D、
D、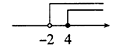 4. 已知 是二元一次方程 的一个解,则 的值为( )A、3 B、-5 C、-3 D、55. 如图,不能判断l1∥l2的条件是( )
4. 已知 是二元一次方程 的一个解,则 的值为( )A、3 B、-5 C、-3 D、55. 如图,不能判断l1∥l2的条件是( ) A、∠1=∠3 B、∠2+∠4=180° C、∠4=∠5 D、∠2=∠36. 下列长度的四根木棒,能与长度分别为2cm和5cm的木棒构成三角形的是( )A、3 B、4 C、7 D、107. 下列命题是真命题的是( )A、同旁内角互补 B、三角形的一个外角等于两个内角的和 C、若a2=b2 , 则a=b D、同角的余角相等8. 如图,已知太阳光线AC和DE是平行的,在同一时刻两根高度相同的木杆竖直插在地面上,在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中判断△ABC≌△DFE的依据是( )
A、∠1=∠3 B、∠2+∠4=180° C、∠4=∠5 D、∠2=∠36. 下列长度的四根木棒,能与长度分别为2cm和5cm的木棒构成三角形的是( )A、3 B、4 C、7 D、107. 下列命题是真命题的是( )A、同旁内角互补 B、三角形的一个外角等于两个内角的和 C、若a2=b2 , 则a=b D、同角的余角相等8. 如图,已知太阳光线AC和DE是平行的,在同一时刻两根高度相同的木杆竖直插在地面上,在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中判断△ABC≌△DFE的依据是( ) A、SAS B、AAS C、HL D、ASA9. 若关于 的不等式组 的所有整数解的和是10,则m的取值范围是( )A、 B、 C、 D、10. 设△ABC的面积为1,如图①将边BC、AC分别2等份,BE1、AD1相交于点O,△AOB的面积记为S1;如图②将边BC、AC分别3等份,BE1、AD1相交于点O,△AOB的面积记为S2;……, 依此类推,则S5的值为( )
A、SAS B、AAS C、HL D、ASA9. 若关于 的不等式组 的所有整数解的和是10,则m的取值范围是( )A、 B、 C、 D、10. 设△ABC的面积为1,如图①将边BC、AC分别2等份,BE1、AD1相交于点O,△AOB的面积记为S1;如图②将边BC、AC分别3等份,BE1、AD1相交于点O,△AOB的面积记为S2;……, 依此类推,则S5的值为( )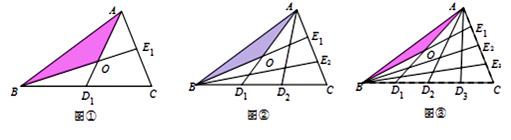 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 肥皂泡额泡壁厚度大约是0.0007mm,0.0007mm用科学记数法表示为mm.12. 分解因式: = .13. 若 ,则 = .14. 内角和是外角和的2倍的多边形是边形.15. 如图,A、B两点分别位于一个池塘的两端,点C是AD的中点,也是BE的中点,若DE=20米,则AB= .
 16. 若多项式 是一个完全平方式,则 的值为 .17. 如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=88°,则∠C的度数为= .
16. 若多项式 是一个完全平方式,则 的值为 .17. 如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=88°,则∠C的度数为= . 18. 若二元一次方程组 的解 , 的值恰好是一个等腰三角形两边的长, 且这个等腰三角形的周长为7,则 的值为 .
18. 若二元一次方程组 的解 , 的值恰好是一个等腰三角形两边的长, 且这个等腰三角形的周长为7,则 的值为 .三、解答题
-
19. 计算:(1)、 ;(2)、20. 因式分解:(1)、 ;(2)、21. 计算题(1)、解方程组: ;(2)、求不等式 的最大整数解.22. 先化简,再求值: ,其中 .23. 已知 .(1)、用含 的代数式表示 的形式为;(2)、若 ,求 的取值范围.24. 如图,在△ABC和△DEF中,已知AB= DE,BE= CF,∠B=∠1,求证:AC∥DF.
 25. 规定两数a,b之间的一种运算,记作(a,b):如果 ,那么(a,b)=c.
25. 规定两数a,b之间的一种运算,记作(a,b):如果 ,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.
(1)、根据上述规定,填空:(3,27)= , (5,1)= , (2, )= .(2)、小明在研究这种运算时发现一个现象:(3n , 4n)=(3,4)小明给出了如下的证明:设(3n , 4n)=x,则(3n)x=4n , 即(3x)n=4n ,
所以3x=4,即(3,4)=x,
所以(3n , 4n)=(3,4).
请你尝试运用这种方法证明下面这个等式:(3,4)+(3,5)=(3,20)
26. 9岁的小芳身高1.36米,她的表姐明年想报考北京的大学.表姐的父母打算今年暑假带着小芳及其表姐先去北京旅游一趟,对北京有所了解.他们四人7月31日下午从无锡出发,1日到4日在北京旅游,7月5日上午返回无锡.无锡与北京之间的火车票和飞机票价如下:火车 (高铁二等座) 全票524元,身高1.1~1.5米的儿童享受半价票;飞机 (普通舱) 全票1240元,已满2周岁未满12周岁的儿童享受半价票.他们往北京的开支预计如下:
住宿费(2人一间的标准房)
伙食费
市内交通费
旅游景点门票费(身高超过1.2米全票)
每间每天x元
每人每天100元
每人每天y元
每人每天120元
假设他们四人在北京的住宿费刚好等于上表所示其他三项费用之和,7月31日和7月5日合计按一天计算,不参观景点,但产生住宿、伙食、市内交通三项费用.
(1)、他们往返都坐火车,结算下来本次旅游总共开支了13668元,求x,y的值;(2)、若去时坐火车,回来坐飞机,且飞机成人票打五五折,其他开支不变,他们准备了14000元,是否够用? 如果不够,他们准备不再增加开支,而是压缩住宿的费用,请问他们预定的标准间房价每天不能超过多少元?