山东省青岛市2018届数学中考模拟试卷（二）
试卷更新日期：2018-07-17 类型：中考模拟
一、单选题
-
1. 实数b满|b|＜3，并且有实数a，a＜b恒成立，a的取值范围是（ ）A、小于或等于3的实数 B、小于3的实数 C、小于或等于﹣3的实数 D、小于﹣3的实数2. 新亚商城春节期间，开设一种摸奖游戏，中一等奖的机会为20万分之一，用科学记数法表示为（ ）A、2×10﹣5 B、5×10﹣6 C、5×10﹣5 D、2×10﹣63. 下图中是中心对称图形而不是轴对称图形的共有（ ）
A、1个 B、2个 C、3个 D、4个4. 已知25x=2000，80y=2000，则 等于（ ）A、2 B、1 C、 D、5. 平面直角坐标系中，将三角形各点的纵坐标都减去﹣3，横坐标保持不变，所得图形与原图形相比（ ）A、向上平移了3个单位 B、向下平移了3个单位 C、向右平移了3个单位 D、向左平移了3个单位6. 在今年抗震赈灾活动中，小明统计了自己所在学校的甲、乙两班的捐款情况，得到三个信息：（1）甲班捐款2500元，乙班捐款2700元；（2）乙班平均每人捐款数比甲班平均每人捐款数多 ；（3）甲班比乙班多5人，设甲班有x人，根据以上信息列方程得（ ）
A、 B、 C、 D、7. 如图，正方形ABCD的边AB=1， 和 都是以1为半径的圆弧，则无阴影两部分的面积之差是（ ）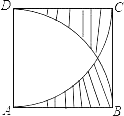
A、 -1 B、1- C、 ﹣1 D、1﹣8. 方程x2+3x﹣1=0的根可视为函数y=x+3的图象与函数 的图象交点的横坐标，那么用此方法可推断出方程x2+2x﹣1=0的实数根x0所在的范围是（ ）A、﹣1＜x0＜0 B、0＜x0＜1 C、1＜x0＜2 D、2＜x0＜3二、填空题
-
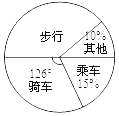
9. 已知：x= ，则 可用含x的有理系数三次多项式来表示为： =10. 如图，某校根据学生上学方式的一次抽样调查结果，绘制出一个未完成的扇形统计图，若该校共有学生1500人，则据此估计步行的有
11. 如图，直线l经过⊙O的圆心O，与⊙O交于A、B两点，点C在⊙O上，∠AOC=30°，点P是直线l上的一个动点（与圆心O不重合），直线CP与⊙O相交于点M，且MP=OM，则满足条件的∠OCP的大小为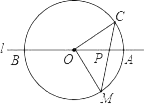
12. 如图，平面直角坐标系中，点A、B分别是x、y轴上的动点，以AB为边作边长为2的正方形ABCD，则OC的最大值为
13. 如图，把一个边长为1的正方形经过三次对折后沿中位线（虚线）剪开，则下图展开得到的图形的面积为
三、解答题
-
14. 验光师测的一组关于近视眼镜的度数y与镜片的焦距x的数据，如表：
y（单位：度）
100
200
400
500
…
x（单位：米）
1.00
0.50
0.25
0.20
…
则y关于x的函数关系式是 ．
15. 如图，已知在△ABC中，∠A=90°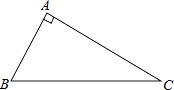
(1)、请用圆规和直尺作出⊙P，使圆心P在AC边上，且与AB，BC两边都相切（保留作 图痕迹，不写作法和证明）．(2)、若∠B=60°，AB=3，求⊙P的面积．
16. 对x，y定义一种新运算T，规定：T（x，y）= （其中a、b均为非零常数），这里等式右边是通常的四则运算，例如：T（0，1）= =b．(1)、已知T（1，﹣1）=﹣2，T（4，2）=1．①求a，b的值；
②若关于m的不等式组 恰好有3个整数解，求实数p的取值范围；
(2)、若T（x，y）=T（y，x）对任意实数x，y都成立（这里T（x，y）和T（y，x）均有意义），则a，b应满足怎样的关系式？
17. 如图，两个可以自由转动的均匀转盘A、B，分别被分成4等分和3等分，并在每份内均标有数字．小花为甲、乙两人设计了一个游戏规则如下：同时自由转动转盘A、B；两个转盘停止后，（如果指针恰好指在分格线上，那么重转一次，直到指针指向某一数字为止），将两个指针所指份内的两个数字相乘，如果得到的积是偶数，那么甲胜；如果得到的积是奇数，则乙胜．但小强认为这样的规则是不公平的．
(1)、请你用一种合适的方法（例如画树状图、列表）帮忙小强说明理由；(2)、请你设计一个公平的规则，并说明理由．18. 如图，为了测量某建筑物CD的高度，先在地面上用测角仪自A处测得建筑物顶部的仰角是α，然后在水平地面上向建筑物前进了m米，此时自B处测得建筑物顶部的仰角是β．已知测角仪的高度是n米，请你计算出该建筑物的高度．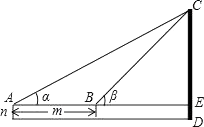
19. 我市某中学举行“中国梦•校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛．两个队各选出的5名选手的决赛成绩（满分为100分）如图所示．
平均数
中位数
众数
初中部
85
高中部
85
100
(1)、根据图示填写表格；(2)、结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
(3)、计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．20. 某校为美化校园，安排甲、乙两个工程队进行绿化．已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍，并且在各自独立完成面积为400m2区域的绿化时，甲队比乙队少用4天．
(1)、求甲、乙两工程队每天能完成绿化的面积分别是多少m2？
(2)、若绿化区域面积为1800m2 ， 学校每天需付给甲队的绿化费用为0.4万元，每天需付给乙队的绿化费用为0.25万元，设安排甲队工作y天，绿化总费用为W万元．①求W与y的函数关系式；
②要使这次的绿化总费用不超过8万元，至少应安排甲队工作多少天？
21. 在▱ABCD中，E是AD上一点，AE=AB，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG．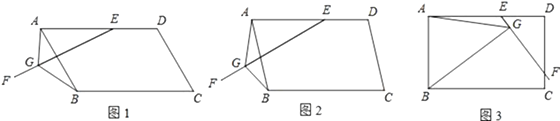
(1)、如图1，当EF与AB相交时，若∠EAB=60°，求证：EG=AG+BG；(2)、如图2，当EF与AB相交时，若∠EAB=α（0°＜α＜90°），请你直接写出线段EG、AG、BG之间的数量关系（用含α的式子表示）；(3)、如图3，当EF与CD相交时，且∠EAB=90°，请你写出线段EG、AG、BG之间的数量关系，并证明你的结论．22. 如图，某日的钱塘江观潮信息如图：
按上述信息，小红将“交叉潮”形成后潮头与乙地之间的距离s（千米）与时间t（分钟）的函数关系用图3表示，其中：“11：40时甲地‘交叉潮’的潮头离乙地12千米”记为点A（0，12），点B坐标为（m，0），曲线BC可用二次函数s= t2+bt+c（b，c是常数）刻画．
(1)、求m的值，并求出潮头从甲地到乙地的速度；
(2)、11：59时，小红骑单车从乙地出发，沿江边公路以0.48千米/分的速度往甲地方向去看潮，问她几分钟后与潮头相遇？(3)、相遇后，小红立即调转车头，沿江边公路按潮头速度与潮头并行，但潮头过乙地后均匀加速，而单车最高速度为0.48千米/分，小红逐渐落后．问小红与潮头相遇到落后潮头1.8千米共需多长时间？（潮水加速阶段速度v=v0+ （t﹣30），v0是加速前的速度）．23. 课本中有一探究活动：如图1，有甲、乙两个三角形，甲三角形内角分别为10°，20°，150°；乙三角形内角分别为80°，25°，75°．你能把每一个三角形分成两个等腰三角形吗？画一画，并标出每个等腰三角形顶角的度数．
(1)、小明按要求画出了图1中甲图的分割线，请你帮他作出图1中乙图的分割线； （1）以80°角的顶点为圆心，夹80°角的较短边为半径画弧，该弧与夹80°角的较长边相较于一点，然后连接这点与75°角的顶点，这条线就把原三角形分成两个等腰三角形，其中一个等腰三角形的顶角是80°，另一个等腰三角形的顶角是130°；
(2)、小明进一步探究发现：能将一个顶角为108°的等腰三角形分成三个等腰三角形；请在图2中用两种不同的方法画出分割线，并标注每个等腰三角形顶角的度数；（若两种方法分得的三角形成3对全等三角形，则视为同一种方法）
24. 已知：如图，在梯形ABCD中，AB∥CD，∠D=90°，AD=CD=2，点E在边AD上（不与点A、D重合），∠CEB=45°，EB与对角线AC相交于点F，设DE=x．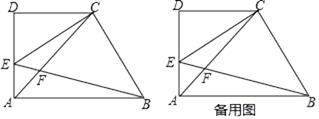
(1)、用含x的代数式表示线段CF的长；
(2)、如果把△CAE的周长记作C△CAE ， △BAF的周长记作C△BAF ， 设 =y，求y关于x的函数关系式，并写出它的定义域；(3)、当∠ABE的正切值是 时，求AB的长．