山东省聊城市2018届九年级中考数学全真模拟试卷
试卷更新日期:2018-07-13 类型:中考模拟
一、单选题
-
1. ﹣2017的倒数是( )A、 B、﹣ C、2017 D、﹣20172. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,直线l1∥l2 , 等腰Rt△ABC的直角顶点C在l1上,顶点A在l2上,若∠β=14°,则∠α=( )
3. 如图,直线l1∥l2 , 等腰Rt△ABC的直角顶点C在l1上,顶点A在l2上,若∠β=14°,则∠α=( )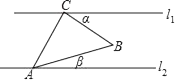 A、31° B、45° C、30° D、59°4. 将0.000 102用科学记数法表示为( )A、1.02×10﹣4 B、1.02×I0﹣5 C、1.02×10﹣6 D、102×10﹣35. 点P(x﹣1,x+1)不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在下列四个几何体中,从正面、左面、上面看不完全相同的是( )
A、31° B、45° C、30° D、59°4. 将0.000 102用科学记数法表示为( )A、1.02×10﹣4 B、1.02×I0﹣5 C、1.02×10﹣6 D、102×10﹣35. 点P(x﹣1,x+1)不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在下列四个几何体中,从正面、左面、上面看不完全相同的是( )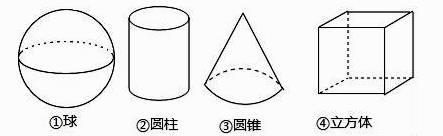 A、①② B、②③ C、①④ D、②④7. 在平面直角坐标系xOy中,经过点(sin45°,cos30°)的直线,与以原点为圆心,2为半径的圆的位置关系是( )
A、①② B、②③ C、①④ D、②④7. 在平面直角坐标系xOy中,经过点(sin45°,cos30°)的直线,与以原点为圆心,2为半径的圆的位置关系是( )
A、相交 B、相切 C、相离 D、以上三者都有可能8. 下列各函数中,y随x增大而增大的是( )A、y=﹣x+1 B、 C、y=x2+1 D、y=2x﹣39. 已知函数y=ax2+bx+c,当y>0时, .则函数y=cx2﹣bx+a的图象可能是下图中的( )
A、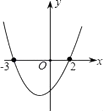 B、
B、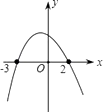 C、
C、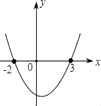 D、
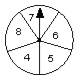
D、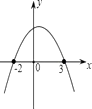 10. 如图,是两个各自分割均匀的转盘,同时转动两个转盘,转盘停止时(若指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止),两个指针所指区域的数字和为偶数的概率是( )
10. 如图,是两个各自分割均匀的转盘,同时转动两个转盘,转盘停止时(若指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止),两个指针所指区域的数字和为偶数的概率是( )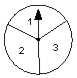
 A、 B、 C、 D、11. 已知方程x2+2x﹣1=0的两根分别是x1 , x2 , 则 =( )A、2 B、﹣2 C、﹣6 D、612. 如图,下列图形均是完全相同的点按照一定的规律所组成的,第①个图形中一共有3个点,第②个图形中一共有8个点,第③个图形中一共有15个点,…,按此规律排列下去,第9个图形中点的个数是( )
A、 B、 C、 D、11. 已知方程x2+2x﹣1=0的两根分别是x1 , x2 , 则 =( )A、2 B、﹣2 C、﹣6 D、612. 如图,下列图形均是完全相同的点按照一定的规律所组成的,第①个图形中一共有3个点,第②个图形中一共有8个点,第③个图形中一共有15个点,…,按此规律排列下去,第9个图形中点的个数是( )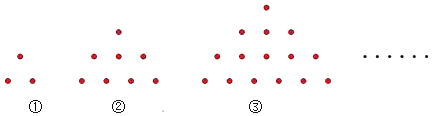 A、80 B、89 C、99 D、109
A、80 B、89 C、99 D、109二、填空题
-
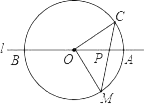
13. 2﹣1+ = .14. 如图,直线l经过⊙O的圆心O,与⊙O交于A、B两点,点C在⊙O上,∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于点M,且MP=OM,则满足条件的∠OCP的大小为 .
 15. 如图,将一张矩形纸片ABCD沿对角线BD折叠,点C的对应点为C′,再将所折得的图形沿EF折叠,使得点D和点A重合.若AB=3,BC=4,则折痕EF的长为
15. 如图,将一张矩形纸片ABCD沿对角线BD折叠,点C的对应点为C′,再将所折得的图形沿EF折叠,使得点D和点A重合.若AB=3,BC=4,则折痕EF的长为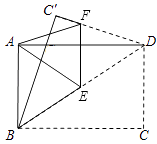 16. 如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为米.
16. 如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为米.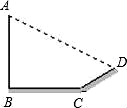 17. 如图,平面直角坐标系中,A(﹣3,0)B(0,4)把△AOB按如图标记的方式连续做旋转变换,这样得到的第2017个三角形中,O点的对应点的坐标为 .
17. 如图,平面直角坐标系中,A(﹣3,0)B(0,4)把△AOB按如图标记的方式连续做旋转变换,这样得到的第2017个三角形中,O点的对应点的坐标为 .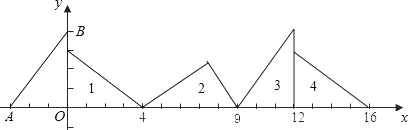
三、解答题
-
18. (y–z)2+(x–y)2+(z–x)2=(y+z–2x)2+(z+x–2y)2+(x+y–2z)2 . 求 的值.19. 为了提高学生书写汉字的能力,增强保护汉子的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为 (分),且 ,将其按分数段分为五组,绘制出以下不完整表格:
组别
成绩 (分)
频数(人数)
频率
一
2
0.04
二
10
0.2
三
14
b
四
a
0.32
五
8
0.16
请根据表格提供的信息,解答以下问题:
(1)、本次决赛共有名学生参加;
(2)、直接写出表中a= , b=;
(3)、请补全下面相应的频数分布直方图;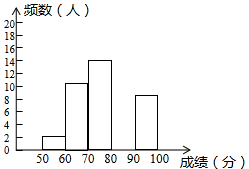 (4)、若决赛成绩不低于80分为优秀,则本次大赛的优秀率为。
(4)、若决赛成绩不低于80分为优秀,则本次大赛的优秀率为。
20. 在▱ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.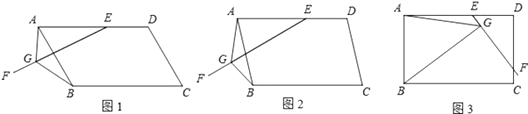 (1)、如图1,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;(2)、如图2,当EF与AB相交时,若∠EAB=α(0°<α<90°),请你直接写出线段EG、AG、BG之间的数量关系(用含α的式子表示);(3)、如图3,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.21. 甲、乙两公司各为“希望工程”捐款2000元.已知乙公司比甲公司人均多捐20元,且乙公司的人数是甲公司人数的 ,问甲、乙两公司人均捐款各多少元?
(1)、如图1,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;(2)、如图2,当EF与AB相交时,若∠EAB=α(0°<α<90°),请你直接写出线段EG、AG、BG之间的数量关系(用含α的式子表示);(3)、如图3,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.21. 甲、乙两公司各为“希望工程”捐款2000元.已知乙公司比甲公司人均多捐20元,且乙公司的人数是甲公司人数的 ,问甲、乙两公司人均捐款各多少元?
22. 如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是α,然后在水平地面上向建筑物前进了m米,此时自B处测得建筑物顶部的仰角是β.已知测角仪的高度是n米,请你计算出该建筑物的高度.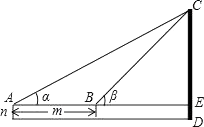 23. 如图,一次函数y=k1x+b与反比例函数y= 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
23. 如图,一次函数y=k1x+b与反比例函数y= 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.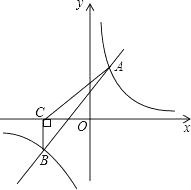 (1)、求一次函数与反比例函数的解析式;
(1)、求一次函数与反比例函数的解析式;
(2)、根据所给条件,请直接写出不等式k1x+b> 的解集;(3)、若P(p,y1),Q(﹣2,y2)是函数y= 图象上的两点,且y1≥y2 , 求实数p的取值范围.24. 如图,在△ABC中,∠ABC=90°,⊙O是△ABC外接圆,点D是圆上一点,点D、B分别在AC两侧,且BD=BC,连接AD、BD、OD、CD,延长CB到点P,使∠APB=∠DCB.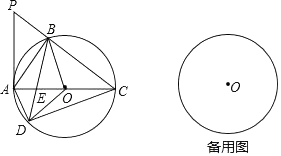 (1)、求证:AP为⊙O的切线;(2)、若⊙O的半径为1,当△OED是直角三角形时,求△ABC的面积;
(1)、求证:AP为⊙O的切线;(2)、若⊙O的半径为1,当△OED是直角三角形时,求△ABC的面积;
(3)、若△BOE、△DOE、△AED的面积分别为a、b、c,试探究a、b、c之间的等量关系式,并说明理由.25. 已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b. (1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)、直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)、a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.