台湾省2018年中考数学试卷
试卷更新日期:2018-07-12 类型:中考真卷
一、选择题
-
1. 下列选项中的图形有一个为轴对称图形,判断此形为何?( )A、
 B、
B、 C、
C、 D、
D、 2. 已知a=( ﹣ )﹣ ,b= ﹣( ﹣ ),c= ﹣ ﹣ ,判断下列叙述何者正确?( )A、a=c,b=c B、a=c,b≠c C、a≠c,b=c D、a≠c,b≠c3. 已知坐标平面上,一次函数y=3x+a的图形通过点(0,﹣4),其中a为一数,求a的值为何?( )A、﹣12 B、﹣4 C、4 D、124. 已知某文具店贩售的笔记本每本售价均相等且超过10元,小锦和小勤在此文具店分别购买若干本笔记本.若小锦购买笔记本的花费为36元,则小勤购买笔记本的花费可能为下列何者?( )A、16元 B、27元 C、30元 D、48元5. 若二元一次联立方程式 的解为x=a,y=b,则a+b之值为何?( )
2. 已知a=( ﹣ )﹣ ,b= ﹣( ﹣ ),c= ﹣ ﹣ ,判断下列叙述何者正确?( )A、a=c,b=c B、a=c,b≠c C、a≠c,b=c D、a≠c,b≠c3. 已知坐标平面上,一次函数y=3x+a的图形通过点(0,﹣4),其中a为一数,求a的值为何?( )A、﹣12 B、﹣4 C、4 D、124. 已知某文具店贩售的笔记本每本售价均相等且超过10元,小锦和小勤在此文具店分别购买若干本笔记本.若小锦购买笔记本的花费为36元,则小勤购买笔记本的花费可能为下列何者?( )A、16元 B、27元 C、30元 D、48元5. 若二元一次联立方程式 的解为x=a,y=b,则a+b之值为何?( )
A、24 B、0 C、﹣4 D、﹣86. 已知甲、乙两袋中各装有若干颗球,其种类与数量如表所示.今阿冯打算从甲袋中抽出一颗球,小潘打算从乙袋中抽出一颗球,若甲袋中每颗球被抽出的机会相等,且乙袋中每颗球被抽出的机会相等,则下列叙述何者正确?( )甲袋
乙袋
红球
2颗
4颗
黄球
2颗
2颗
绿球
1颗
4颗
总计
5颗
10颗
A、阿冯抽出红球的机率比小潘抽出红球的机率大 B、阿冯抽出红球的机率比小潘抽出红球的机率小 C、阿冯抽出黄球的机率比小潘抽出黄球的机率大 D、阿冯抽出黄球的机率比小潘抽出黄球的机率小7. 算式 ×( ﹣1)之值为何?( )A、 B、 C、2- D、18. 若一元二次方程式x2﹣8x﹣3×11=0的两根为a、b,且a>b,则a﹣2b之值为何?( )
A、﹣25 B、﹣19 C、5 D、179. 如图,△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧交AC于E点,若∠A=60°,∠B=100°,BC=4,则扇形BDE的面积为何?( ) A、 B、 C、 D、10. 如图为大兴电器行的促销活动传单,已知促销第一天美食牌微波炉卖出10台,且其销售额为61000元,若活动期间此款微波炉总共卖出50台,则其总销售额为多少元?( )
A、 B、 C、 D、10. 如图为大兴电器行的促销活动传单,已知促销第一天美食牌微波炉卖出10台,且其销售额为61000元,若活动期间此款微波炉总共卖出50台,则其总销售额为多少元?( ) A、305000 B、321000 C、329000 D、34200011. 如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )
A、305000 B、321000 C、329000 D、34200011. 如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )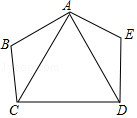 A、115 B、120 C、125 D、13012. 如图为O,A,B,C四点在数线上的位置图,其中O为原点,且AC=1,OA=OB,若C点所表示的数为x,则B点所表示的数与下列何者相等?( )
A、115 B、120 C、125 D、13012. 如图为O,A,B,C四点在数线上的位置图,其中O为原点,且AC=1,OA=OB,若C点所表示的数为x,则B点所表示的数与下列何者相等?( )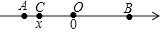 A、﹣(x+1) B、﹣(x﹣1) C、x+1 D、x﹣113. 如图的宣传单为莱克印刷公司设计与印刷卡片计价方式的说明,妮娜打算请此印刷公司设计一款母亲节卡片并印刷,她再将卡片以每张15元的价格贩售.若利润等于收入扣掉成本,且成本只考虑设计费与印刷费,则她至少需印多少张卡片,才可使得卡片全数售出后的利润超过成本的2成?( )
A、﹣(x+1) B、﹣(x﹣1) C、x+1 D、x﹣113. 如图的宣传单为莱克印刷公司设计与印刷卡片计价方式的说明,妮娜打算请此印刷公司设计一款母亲节卡片并印刷,她再将卡片以每张15元的价格贩售.若利润等于收入扣掉成本,且成本只考虑设计费与印刷费,则她至少需印多少张卡片,才可使得卡片全数售出后的利润超过成本的2成?( ) A、112 B、121 C、134 D、14314. 如图,I点为△ABC的内心,D点在BC上,且ID⊥BC,若∠B=44°,∠C=56°,则∠AID的度数为何?( )
A、112 B、121 C、134 D、14314. 如图,I点为△ABC的内心,D点在BC上,且ID⊥BC,若∠B=44°,∠C=56°,则∠AID的度数为何?( ) A、174 B、176 C、178 D、18015. 如图为一直棱柱,其底面是三边长为5、12、13的直角三角形.若下列选项中的图形均由三个矩形与两个直角三角形组合而成,且其中一个为如图的直棱柱的展开图,则根据图形中标示的边长与直角记号判断,此展开图为何?( )
A、174 B、176 C、178 D、18015. 如图为一直棱柱,其底面是三边长为5、12、13的直角三角形.若下列选项中的图形均由三个矩形与两个直角三角形组合而成,且其中一个为如图的直棱柱的展开图,则根据图形中标示的边长与直角记号判断,此展开图为何?( )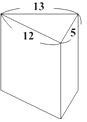 A、
A、 B、
B、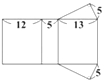 C、
C、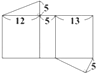 D、
D、 16. 若小舒从1~50的整数中挑选4个数,使其由小到大排序后形成一等差数列,且4个数中最小的是7,则下列哪一个数不可能出现在小舒挑选的数之中?( )A、20 B、25 C、30 D、3517. 已知a=3.1×10﹣4 , b=5.2×10﹣8 , 判断下列关于a﹣b之值的叙述何者正确?( )
16. 若小舒从1~50的整数中挑选4个数,使其由小到大排序后形成一等差数列,且4个数中最小的是7,则下列哪一个数不可能出现在小舒挑选的数之中?( )A、20 B、25 C、30 D、3517. 已知a=3.1×10﹣4 , b=5.2×10﹣8 , 判断下列关于a﹣b之值的叙述何者正确?( )
A、比1大 B、介于0、1之间 C、介于﹣1、0之间 D、比﹣1小18. 如图,锐角三角形ABC中,BC>AB>AC,甲、乙两人想找一点P,使得∠BPC与∠A互补,其作法分别如下:(甲)以A为圆心,AC长为半径画弧交AB于P点,则P即为所求;
(乙)作过B点且与AB垂直的直线l,作过C点且与AC垂直的直线,交l于P点,则P即为所求对于甲、乙两人的作法,下列叙述何者正确?( )
 A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确19. 已知甲、乙两班的学生人数相同,如图为两班某次数学小考成绩的盒状图,若甲班、乙班学生小考成绩的中位数分别为a、b;甲班、乙班中小考成绩超过80分的学生人数分别为c、d,则下列a、b、c、d的大小关系,何者正确?( )
A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确19. 已知甲、乙两班的学生人数相同,如图为两班某次数学小考成绩的盒状图,若甲班、乙班学生小考成绩的中位数分别为a、b;甲班、乙班中小考成绩超过80分的学生人数分别为c、d,则下列a、b、c、d的大小关系,何者正确?( ) A、a>b,c>d B、a>b,c<d C、a<b,c>d D、a<b,c<d20. 如图1的矩形ABCD中,有一点E在AD上,今以BE为折线将A点往右折,如图2所示,再作过A点且与CD垂直的直线,交CD于F点,如图3所示,若AB=6 ,BC=13,∠BEA=60°,则图3中AF的长度为何?( )
A、a>b,c>d B、a>b,c<d C、a<b,c>d D、a<b,c<d20. 如图1的矩形ABCD中,有一点E在AD上,今以BE为折线将A点往右折,如图2所示,再作过A点且与CD垂直的直线,交CD于F点,如图3所示,若AB=6 ,BC=13,∠BEA=60°,则图3中AF的长度为何?( ) A、2 B、4 C、2 D、421. 已知坐标平面上有一直线L,其方程式为y+2=0,且L与二次函数y=3x2+a的图形相交于A,B两点:与二次函数y=﹣2x2+b的图形相交于C,D两点,其中a、b为整数.若AB=2,CD=4.则a+b之值为何?( )
A、2 B、4 C、2 D、421. 已知坐标平面上有一直线L,其方程式为y+2=0,且L与二次函数y=3x2+a的图形相交于A,B两点:与二次函数y=﹣2x2+b的图形相交于C,D两点,其中a、b为整数.若AB=2,CD=4.则a+b之值为何?( )
A、1 B、9 C、16 D、2422. 如图,两圆外切于P点,且通过P点的公切线为L,过P点作两直线,两直线与两圆的交点为A,B,C,D,其位置如图所示,若AP=10,CP=9,则下列角度关系何者正确?( ) A、∠PBD>∠PAC B、∠PBD<∠PAC C、∠PBD>∠PDB D、∠PBD<∠PDB23. 小柔要榨果汁,她有苹果、芭乐、柳丁三种水果,且其颗数比为9:7:6,小柔榨完果汁后,苹果、芭乐、柳丁的颗数比变为6:3:4,已知小柔榨果汁时没有使用柳丁,关于她榨果汁时另外两种水果的使用情形,下列叙述何者正确?( )A、只使用苹果 B、只使用芭乐 C、使用苹果及芭乐,且使用的苹果颗数比使用的芭乐颗数多 D、使用苹果及芭乐,且使用的芭乐颗数比使用的苹果颗数多24. 如图,△ABC,△FGH中,D,E两点分别在AB,AC上,F点在DE上,G、H两点在BC上,且DE∥BC,FG∥AB,FH∥AC,若BG:GH:HC=4:6:5,则△ADE与△FGH的面积比为何?( )
A、∠PBD>∠PAC B、∠PBD<∠PAC C、∠PBD>∠PDB D、∠PBD<∠PDB23. 小柔要榨果汁,她有苹果、芭乐、柳丁三种水果,且其颗数比为9:7:6,小柔榨完果汁后,苹果、芭乐、柳丁的颗数比变为6:3:4,已知小柔榨果汁时没有使用柳丁,关于她榨果汁时另外两种水果的使用情形,下列叙述何者正确?( )A、只使用苹果 B、只使用芭乐 C、使用苹果及芭乐,且使用的苹果颗数比使用的芭乐颗数多 D、使用苹果及芭乐,且使用的芭乐颗数比使用的苹果颗数多24. 如图,△ABC,△FGH中,D,E两点分别在AB,AC上,F点在DE上,G、H两点在BC上,且DE∥BC,FG∥AB,FH∥AC,若BG:GH:HC=4:6:5,则△ADE与△FGH的面积比为何?( )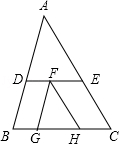 A、2:1 B、3:2 C、5:2 D、9:425. 某商店将巧克力包装成方形、圆形礼盒出售,且每盒方形礼盒的价钱相同,每盒圆形礼盒的价钱相同.阿郁原先想购买3盒方形礼盒和7盒圆形礼盒,但他身上的钱会不足240元,如果改成购买7盒方形礼盒和3盒形礼盒,他身上的钱会剩下240元.若阿郁最后购买10盒方形礼盒,则他身上的钱会剩下多少元?( )
A、2:1 B、3:2 C、5:2 D、9:425. 某商店将巧克力包装成方形、圆形礼盒出售,且每盒方形礼盒的价钱相同,每盒圆形礼盒的价钱相同.阿郁原先想购买3盒方形礼盒和7盒圆形礼盒,但他身上的钱会不足240元,如果改成购买7盒方形礼盒和3盒形礼盒,他身上的钱会剩下240元.若阿郁最后购买10盒方形礼盒,则他身上的钱会剩下多少元?( )
A、360 B、480 C、600 D、72026. 如图,坐标平面上,A,B两点分别为圆P与x轴、y轴的交点,有一直线L通过P点且与AB垂直,C点为L与y轴的交点.若A,B,C的坐标分别为(a,0),(0,4),(0,﹣5),其中a<0,则a的值为何?( ) A、﹣2 B、﹣2 C、﹣8 D、﹣7
A、﹣2 B、﹣2 C、﹣8 D、﹣7二、非选择题
-
27. 一个箱子内有4颗相同的球,将4颗球分别标示号码1、2、3、4,今翔翔以每次从箱子内取一颗球且取后放回的方式抽取,并预计取球10次,现已取了8次,取出的结果如表所列:
次数
第1次
第2次
第3次
第4次
第5次
第6次
第7次
第8次
第9次
第10次
号码
1
3
4
4
2
1
4
1
若每次取球时,任一颗球被取到的机会皆相等,且取出的号码即为得分,请回答下列问题:
(1)、请求出第1次至第8次得分的平均数.(2)、承(1),翔翔打算依计划继续从箱子取球2次,请判断是否可能发生「这10次得分的平均数不小于2.2,且不大于2.4」的情形?若有可能,请计算出发生此情形的机率,并完整写出你的解题过程;若不可能,请完整说明你的理由.
28. 嘉嘉参加机器人设计活动,需操控机器人在5×5的方格棋盘上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1 , R2 , R3 , 其行经位置如图与表所示:路径
编号
图例
行径位置
第一条路径
R1
_
A→C→D→B
第二条路径
R2
…
A→E→D→F→B
第三条路径
R3
▂
A→G→B
已知A、B、C、D、E、F、G七点皆落在格线的交点上,且两点之间的路径皆为直线,在无法使用任何工具测量的条件下,请判断R1、R2、R3这三条路径中,最长与最短的路径分别为何?请写出你的答案,并完整说明理由.
