湖北省襄阳市2018年中考数学试卷
试卷更新日期:2018-07-12 类型:中考真卷
一、选择题
-
1. ﹣2的相反数为( )A、2 B、 C、﹣2 D、—2. 近几年,襄阳市经济呈现稳中有进,稳中向好的态势,2017年GDP突破4000亿元大关,4000亿这个数用科学记数法表示为( )A、4×1012 B、4×1011 C、0.4×1012 D、40×10113. 如图,把一块三角板的直角顶点放在一直尺的一边上,若∠1=50°,则∠2的度数为( )
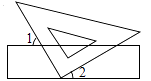 A、55° B、50° C、45° D、40°4. 下列运算正确的是( )A、a2+a2=2a4 B、a6÷a2=a3 C、(﹣a3)2=a6 D、(ab)2=ab25. 不等式组 的解集为( )A、x> B、x>1 C、 <x<1 D、空集6.
A、55° B、50° C、45° D、40°4. 下列运算正确的是( )A、a2+a2=2a4 B、a6÷a2=a3 C、(﹣a3)2=a6 D、(ab)2=ab25. 不等式组 的解集为( )A、x> B、x>1 C、 <x<1 D、空集6.一个几何体的三视图如图所示,则这个几何体是( )
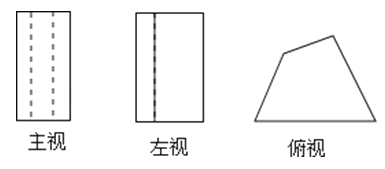 A、
A、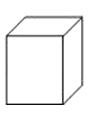 B、
B、 C、
C、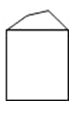 D、
D、 7. 如图,在△ABC中,分别以点A和点C为圆心,大于 AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=3cm,△ABD的周长为13cm,则△ABC的周长为( )
7. 如图,在△ABC中,分别以点A和点C为圆心,大于 AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=3cm,△ABD的周长为13cm,则△ABC的周长为( )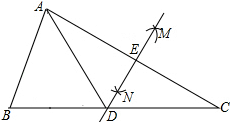 A、16cm B、19cm C、22cm D、25cm8. 下列语句所描述的事件是随机事件的是( )A、任意画一个四边形,其内角和为180° B、经过任意点画一条直线 C、任意画一个菱形,是中心对称图形 D、过平面内任意三点画一个圆9. 已知二次函数y=x2﹣x+ m﹣1的图象与x轴有交点,则m的取值范围是( )A、m≤5 B、m≥2 C、m<5 D、m>210. 如图,点A,B,C,D都在半径为2的⊙O上,若OA⊥BC,∠CDA=30°,则弦BC的长为( )
A、16cm B、19cm C、22cm D、25cm8. 下列语句所描述的事件是随机事件的是( )A、任意画一个四边形,其内角和为180° B、经过任意点画一条直线 C、任意画一个菱形,是中心对称图形 D、过平面内任意三点画一个圆9. 已知二次函数y=x2﹣x+ m﹣1的图象与x轴有交点,则m的取值范围是( )A、m≤5 B、m≥2 C、m<5 D、m>210. 如图,点A,B,C,D都在半径为2的⊙O上,若OA⊥BC,∠CDA=30°,则弦BC的长为( ) A、4 B、2 C、 D、2
A、4 B、2 C、 D、2二、填空题
-
11. 计算:|1﹣ |= .12. 计算 的结果是 .13. 我国古代数学著作《九章算术》中有一道阐述“盈不足术”的问题,译文为:“现有几个人共同购买一个物品,每人出8元,则多3元;每人出7元,则差4元.问这个物品的价格是多少元?”该物品的价格是元.
14. 一组数据3,2,3,4,x的平均数是3,则它的方差是 .15. 已知CD是△ABC的边AB上的高,若CD= ,AD=1,AB=2AC,则BC的长为 .16. 如图,将面积为32 的矩形ABCD沿对角线BD折叠,点A的对应点为点P,连接AP交BC于点E.若BE= ,则AP的长为 .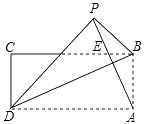
三、解答题
-
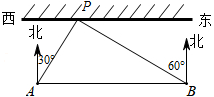
17. 先化简,再求值:(x+y)(x﹣y)+y(x+2y)﹣(x﹣y)2 , 其中x=2+ ,y=2﹣ .18. 为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).
 19. “品中华诗词,寻文化基因”.某校举办了第二届“中华诗词大赛”,将该校八年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
19. “品中华诗词,寻文化基因”.某校举办了第二届“中华诗词大赛”,将该校八年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.频数分布统计表
组别
成绩x(分)
人数
百分比
A
60≤x<70
8
20%
B
70≤x<80
16
m%
C
80≤x<90
a
30%
D
90≤<x≤100
4
10%
请观察图表,解答下列问题:
 (1)、表中a= , m=;(2)、补全频数分布直方图;(3)、D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率为 .20. 正在建设的“汉十高铁”竣工通车后,若襄阳至武汉段路程与当前动车行驶的路程相等,约为325千米,且高铁行驶的速度是当前动车行驶速度的2.5倍,则从襄阳到武汉乘坐高铁比动车所用时间少1.5小时.求高铁的速度.
(1)、表中a= , m=;(2)、补全频数分布直方图;(3)、D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率为 .20. 正在建设的“汉十高铁”竣工通车后,若襄阳至武汉段路程与当前动车行驶的路程相等,约为325千米,且高铁行驶的速度是当前动车行驶速度的2.5倍,则从襄阳到武汉乘坐高铁比动车所用时间少1.5小时.求高铁的速度.
21. 如图,已知双曲线y1= 与直线y2=ax+b交于点A(﹣4,1)和点B(m,﹣4). (1)、求双曲线和直线的解析式;(;(2)、直接写出线段AB的长和y1>y2时x的取值范围.22. 如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,E为⊙O上一点,过点E作直线DC分别交AM,BN于点D,C,且CB=CE.
(1)、求双曲线和直线的解析式;(;(2)、直接写出线段AB的长和y1>y2时x的取值范围.22. 如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,E为⊙O上一点,过点E作直线DC分别交AM,BN于点D,C,且CB=CE.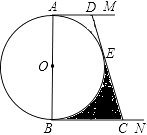 (1)、求证:DA=DE;(2)、若AB=6,CD=4 ,求图中阴影部分的面积.23. 襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).(1)、m= , n=;(2)、求销售蓝莓第几天时,当天的利润最大?最大利润是多少?(3)、在销售蓝莓的30天中,当天利润不低于870元的共有多少天?24. 如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)、求证:DA=DE;(2)、若AB=6,CD=4 ,求图中阴影部分的面积.23. 襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).(1)、m= , n=;(2)、求销售蓝莓第几天时,当天的利润最大?最大利润是多少?(3)、在销售蓝莓的30天中,当天利润不低于870元的共有多少天?24. 如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.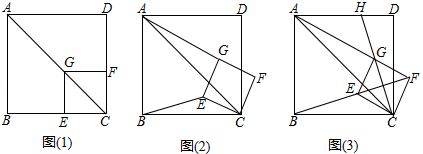 (1)、证明与推断:
(1)、证明与推断:①求证:四边形CEGF是正方形;②推断: AG∶BE的值为 :
(2)、探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)、拓展与运用:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2 ,则BC= .
25. 直线y=﹣ x+3交x轴于点A,交y轴于点B,顶点为D的抛物线y=﹣ x2+2mx﹣3m经过点A,交x轴于另一点C,连接BD,AD,CD,如图所示.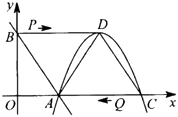 (1)、直接写出抛物线的解析式和点A,C,D的坐标;
(1)、直接写出抛物线的解析式和点A,C,D的坐标;
(2)、动点P在BD上以每秒2个单位长的速度由点B向点D运动,同时动点Q在CA上以每秒3个单位长的速度由点C向点A运动,当其中一个点到达终点停止运动时,另一个点也随之停止运动,设运动时间为t秒.PQ交线段AD于点E.①当∠DPE=∠CAD时,求t的值;
②过点E作EM⊥BD,垂足为点M,过点P作PN⊥BD交线段AB或AD于点N,当PN=EM时,求t的值.