贵州省(黔东南,黔南,黔西南)2018年中考数学试卷
试卷更新日期:2018-07-12 类型:中考真卷
一、选择题
-
1. 下列四个数中,最大的数是( )A、﹣2 B、﹣1 C、0 D、2. 如图的几何体是由四个大小相同的正方体组成的,它的俯视图是( )
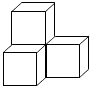 A、
A、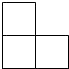 B、
B、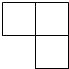 C、
C、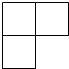 D、
D、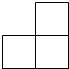 3. 据统计,近十年中国累积节能1570000万吨标准煤,1570000这个数用科学记数法表示为( )A、0157×107 B、1.57×106 C、1.57×107 D、1.57×1084. 如图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC=( )
3. 据统计,近十年中国累积节能1570000万吨标准煤,1570000这个数用科学记数法表示为( )A、0157×107 B、1.57×106 C、1.57×107 D、1.57×1084. 如图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC=( )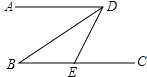 A、30° B、60° C、90° D、120°5. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、
A、30° B、60° C、90° D、120°5. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列运算正确的是( )A、3a2﹣2a2=a2 B、﹣(2a)2=﹣2a2 C、(a+b)2=a2+b2 D、﹣2(a﹣1)=﹣2a+17. 下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
6. 下列运算正确的是( )A、3a2﹣2a2=a2 B、﹣(2a)2=﹣2a2 C、(a+b)2=a2+b2 D、﹣2(a﹣1)=﹣2a+17. 下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )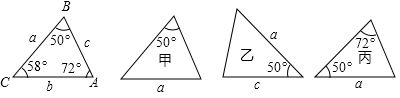 A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙8. 施工队要铺设1000米的管道,因在中考期间需停工2天,每天要比原计划多施工30米才能按时完成任务.设原计划每天施工x米,所列方程正确的是( )
A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙8. 施工队要铺设1000米的管道,因在中考期间需停工2天,每天要比原计划多施工30米才能按时完成任务.设原计划每天施工x米,所列方程正确的是( )
A、 =2 B、 =2 C、 =2 D、 =29. 下列等式正确的是( )A、 =2 B、 =3 C、 =4 D、 =510. 如图在▱ABCD中,已知AC=4cm,若△ACD的周长为13cm,则▱ABCD的周长为( )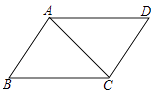 A、26cm B、24cm C、20cm D、18cm
A、26cm B、24cm C、20cm D、18cm二、填空题
-
11. ∠α=35°,则∠α的补角为度.12. 不等式组 的解集是 .13. 如图为洪涛同学的小测卷,他的得分应是分.
 14. 若100个产品中有98个正品,2个次品,从中随机抽取一个,抽到次品的概率是 .15. 某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数 (单位:分)及方差S2 , 如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是 .
14. 若100个产品中有98个正品,2个次品,从中随机抽取一个,抽到次品的概率是 .15. 某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数 (单位:分)及方差S2 , 如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是 .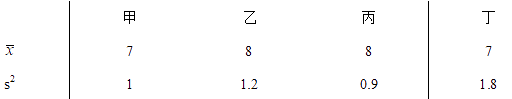 16. 三角形的两边长分别为3和6,第三边的长是方程x2﹣6x+8=0的解,则此三角形周长是 .17. 已知一个菱形的边长为2,较长的对角线长为2 ,则这个菱形的面积是 .18. 已知:二次函数y=ax2+bx+c图象上部分点的横坐标x与纵坐标y的对应值如表格所示,那么它的图象与x轴的另一个交点坐标是 .
16. 三角形的两边长分别为3和6,第三边的长是方程x2﹣6x+8=0的解,则此三角形周长是 .17. 已知一个菱形的边长为2,较长的对角线长为2 ,则这个菱形的面积是 .18. 已知:二次函数y=ax2+bx+c图象上部分点的横坐标x与纵坐标y的对应值如表格所示,那么它的图象与x轴的另一个交点坐标是 .x
…
﹣1
0
1
2
…
y
…
0
3
4
3
…
19. 根据下列各式的规律,在横线处填空:, , , …, ﹣= .
20. 如图,已知在△ABC中,BC边上的高AD与AC边上的高BE交于点F,且∠BAC=45°,BD=6,CD=4,则△ABC的面积为 .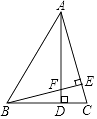
三、解答题(一)
-
21.
(1)、计算:|﹣2|﹣2cos60°+( )﹣1﹣(2018﹣ )0(2)、先化简(1﹣ )• ,再在1、2、3中选取一个适当的数代入求值.四、解答题(二)
-
22. 如图,CE是⊙O的直径,BC切⊙O于点C,连接OB,作ED∥OB交⊙O于点D,BD的延长线与CE的延长线交于点A.
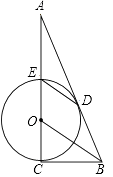 (1)、求证:AB是⊙O的切线;(2)、若⊙O的半径为1,tan∠DEO= ,tan∠A= ,求AE的长.
(1)、求证:AB是⊙O的切线;(2)、若⊙O的半径为1,tan∠DEO= ,tan∠A= ,求AE的长.五、解答题(三)
-
23. 目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
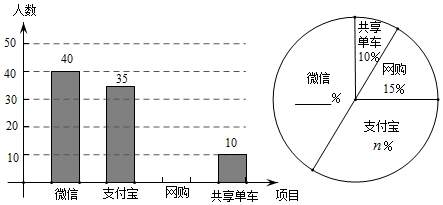 (1)、根据图中信息求出m= , n=;
(1)、根据图中信息求出m= , n=;
(2)、请你帮助他们将这两个统计图补全;(3)、根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
(4)、已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.六、解答题(四)
-
24. 某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
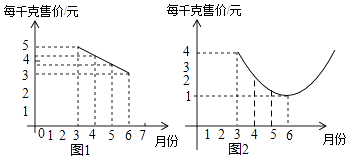 (1)、已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(1)、已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)、哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.(3)、已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
七、阅读材料题
-
25. “分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.
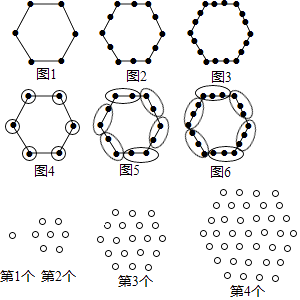
例如:图1有6个点,图2有12个点,图3有18个点,……,按此规律,求图10、图n有多少个点?
(1)、我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图),这样图1中黑点个数是6×1=6个;图2中黑点个数是6×2=12个:图3中黑点个数是6×3=18个;所以容易求出图10、图n中黑点的个数分别是、 .
(2)、请你参考以上“分块计数法”,先将下面的点阵进行分块(画在答题卡上),再完成以下问题:①第5个点阵中有个圆圈;第n个点阵中有个圆圈.
②小圆圈的个数会等于271吗?如果会,请求出是第几个点阵.
八、解答题(五)
-
26. 如图1,已知矩形AOCB,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动.
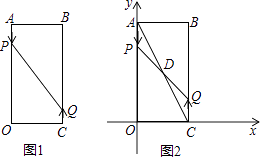 (1)、点P到达终点O的运动时间是s,此时点Q的运动距离是cm;(2)、当运动时间为2s时,P、Q两点的距离为cm;(3)、请你计算出发多久时,点P和点Q之间的距离是10cm;(4)、如图2,以点O为坐标原点,OC所在直线为x轴,OA所在直线为y轴,1cm长为单位长度建立平面直角坐标系,连结AC,与PQ相交于点D,若双曲线y= 过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.
(1)、点P到达终点O的运动时间是s,此时点Q的运动距离是cm;(2)、当运动时间为2s时,P、Q两点的距离为cm;(3)、请你计算出发多久时,点P和点Q之间的距离是10cm;(4)、如图2,以点O为坐标原点,OC所在直线为x轴,OA所在直线为y轴,1cm长为单位长度建立平面直角坐标系,连结AC,与PQ相交于点D,若双曲线y= 过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.
-
-
-
-
-