北京市2018年中考数学试卷
试卷更新日期:2018-07-12 类型:中考真卷
一、选择题
-
1. 下列几何体中,是圆柱的为( )A、
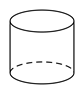 B、
B、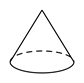 C、
C、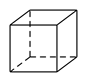 D、
D、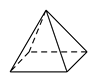 2. 实数 , , 在数轴上的对应点的位置如图所示,则正确的结论是( )
2. 实数 , , 在数轴上的对应点的位置如图所示,则正确的结论是( )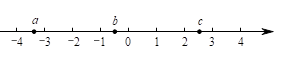 A、 B、 C、 D、3. 方程组 的解为( )A、 B、 C、 D、4. 被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST的反射面总面积相当于35个标准足球场的总面积.已知每个标准足球场的面积为 ,则FAST的反射面积总面积约为( )A、 B、 C、 D、5. 若正多边形的一个外角是 ,则该正多边形的内角和为( )A、 B、 C、 D、6. 如果 ,那么代数式 的值为( )A、 B、 C、 D、7. 跳台滑雪是冬季奥运会比赛项目之一.运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度 (单位: )与水平距离 (单位: )近似满足函数关系 ( ).下图记录了某运动员起跳后的 与 的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为( )
A、 B、 C、 D、3. 方程组 的解为( )A、 B、 C、 D、4. 被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST的反射面总面积相当于35个标准足球场的总面积.已知每个标准足球场的面积为 ,则FAST的反射面积总面积约为( )A、 B、 C、 D、5. 若正多边形的一个外角是 ,则该正多边形的内角和为( )A、 B、 C、 D、6. 如果 ,那么代数式 的值为( )A、 B、 C、 D、7. 跳台滑雪是冬季奥运会比赛项目之一.运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度 (单位: )与水平距离 (单位: )近似满足函数关系 ( ).下图记录了某运动员起跳后的 与 的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为( )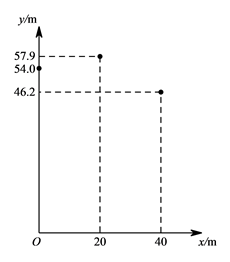 A、 B、 C、 D、8. 如图是老北京城一些地点的分布示意图.在图中,分别以正东、正北方向为 轴、 轴的正方向建立平面直角坐标系,有如下四个结论:
A、 B、 C、 D、8. 如图是老北京城一些地点的分布示意图.在图中,分别以正东、正北方向为 轴、 轴的正方向建立平面直角坐标系,有如下四个结论: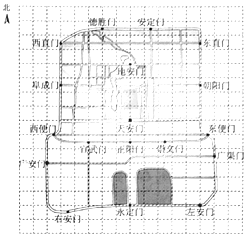
①当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为( , )时,表示左安门的点的坐标为(5, );②当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为( , )时,表示左安门的点的坐标为(10, );③当表示天安门的点的坐标为(1,1),表示广安门的点的坐标为( , )时,表示左安门的点的坐标为( , );④当表示天安门的点的坐标为( , ),表示广安门的点的坐标为( , )时,表示左安门的点的坐标为( , ).上述结论中,所有正确结论的序号是( )
A、①②③ B、②③④ C、①④ D、①②③④二、填空题
-
9. 下图所示的网格是正方形网格, .(填“ ”,“ ”或“ ”)
 10. 若 在实数范围内有意义,则实数 的取值范围是 .11. 用一组 , , 的值说明命题“若 ,则 ”是错误的,这组值可以是 , , .12. 如图,点 , , , 在 上, , , ,则 .
10. 若 在实数范围内有意义,则实数 的取值范围是 .11. 用一组 , , 的值说明命题“若 ,则 ”是错误的,这组值可以是 , , .12. 如图,点 , , , 在 上, , , ,则 . 13. 如图,在矩形 中, 是边 的中点,连接 交对角线 于点 ,若 , ,则 的长为 .
13. 如图,在矩形 中, 是边 的中点,连接 交对角线 于点 ,若 , ,则 的长为 .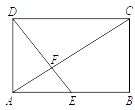 14. 从甲地到乙地有A,B,C三条不同的公交线路.为了解决早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
14. 从甲地到乙地有A,B,C三条不同的公交线路.为了解决早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:公交车用时
公交车用时的频数
线路
合计
A
59
151
166
124
500
B
50
50
122
278
500
C
45
265
167
23
500
早高峰期间,乘坐(填“A”,“B”或“C”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
15. 某公园划船项目收费标准如下:船型
两人船
(限乘两人)
四人船
(限乘四人)
六人船
(限乘六人)
八人船
(限乘八人)
每船租金
(元/小时)
90
100
130
150
某班18名同学一起去该公园划船,若每人划船的时间均为1小时,则租船的总费用最低为元.
16. 2017年,部分国家及经济体在全球的创新综合排名、创新产出排名和创新效率排名情况如图所示,中国创新综合排名全球第22,创新效率排名全球第 .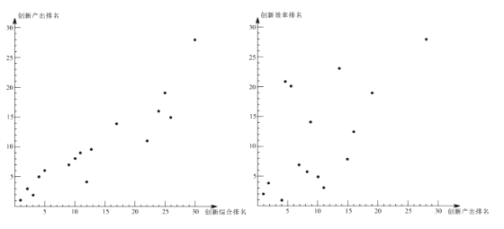
三、解答题
-
17. 下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:直线及直线外一点 .

求作: ,使得 .
作法:如图,

①在直线上取一点 ,作射线 ,以点 为圆心, 长为半径画弧,交 的延长线于点 ;
②在直线上取一点 (不与点 重合),作射线 ,以点 为圆心, 长为半径画弧,交 的延长线于点 ;
③作直线 .
所以直线 就是所求作的直线.
根据小东设计的尺规作图过程,
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明.证明:∵ , ,
∴ ()(填推理的依据).
18. 计算: .19. 解不等式组: .20. 关于 的一元二次方程 .
(1)、当 时,利用根的判别式判断方程根的情况;
(2)、若方程有两个相等的实数根,写出一组满足条件的 , 的值,并求此时方程的根.
21. 如图,在四边形 中, , ,对角线 , 交于点 , 平分 ,过点 作 交 的延长线于点 ,连接 . (1)、求证:四边形 是菱形;(2)、若 , ,求 的长.
(1)、求证:四边形 是菱形;(2)、若 , ,求 的长.
22. 如图, 是 的直径,过 外一点 作 的两条切线 , ,切点分别为 , ,连接 , . (1)、求证: ;
(1)、求证: ;
(2)、连接 , ,若 , , ,求 的长.23. 在平面直角坐标系 中,函数 ( )的图象 经过点 (4,1),直线 与图象 交于点 ,与 轴交于点 .(1)、求 的值;(2)、横、纵坐标都是整数的点叫做整点.记图象 在点 , 之间的部分与线段 , , 围成的区域(不含边界)为 .①当 时,直接写出区域 内的整点个数;
②若区域 内恰有4个整点,结合函数图象,求 的取值范围.
24. 如图, 是 与弦 所围成的图形的内部的一定点, 是弦 上一动点,连接 并延长交 于点 ,连接 .已知 ,设 , 两点间的距离为 , , 两点间的距离为 , , 两点间的距离为 .
小腾根据学习函数的经验,分别对函数 , 随自变量 的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)、按照下表中自变量 的值进行取点、画图、测量,分别得到了 , 与 的几组对应值;0
1
2
3
4
5
6
(2)、在同一平面直角坐标系 中,描出补全后的表中各组数值所对应的点( , ),( , ),并画出函数 , 的图象; (3)、结合函数图象,解决问题:当 为等腰三角形时, 的长度约为 .25. 某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
(3)、结合函数图象,解决问题:当 为等腰三角形时, 的长度约为 .25. 某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息..A课程成绩的频数分布直方图如下(数据分成6组: , , , , , );

.A课程成绩在 这一组是:
70 71 71 71 76 76 77 78 79 79 79
.A,B两门课程成绩的平均数、中位数、众数如下:
课程
平均数
中位数
众数
A
B
70
83
根据以上信息,回答下列问题:
(1)、写出表中 的值;(2)、在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是(填“A”或“B”),理由是;(3)、假设该年级学生都参加此次测试,估计A课程成绩超过 分的人数.
26. 在平面直角坐标系 中,直线 与 轴、 轴分别交于点 , ,抛物线 经过点 ,将点 向右平移5个单位长度,得到点 .(1)、求点 的坐标;
(2)、求抛物线的对称轴;
(3)、若抛物线与线段 恰有一个公共点,结合函数图象,求 的取值范围.27. 如图,在正方形 中, 是边 上的一动点(不与点 , 重合),连接 ,点 关于直线 的对称点为 ,连接 并延长交 于点 ,连接 ,过点 作 交 的延长线于点 ,连接 .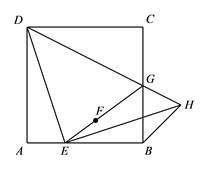 (1)、求证: ;
(1)、求证: ;
(2)、用等式表示线段 与 的数量关系,并证明.28. 对于平面直角坐标系 中的图形 , ,给出如下定义: 为图形 上任意一点, 为图形 上任意一点,如果 , 两点间的距离有最小值,那么称这个最小值为图形 , 间的“闭距离”,记作 ( , ).已知点 ( ,6), ( , ), (6, ).
(1)、求 (点 , );
(2)、记函数 ( , )的图象为图形 ,若 ( , ) ,直接写出 的取值范围;
(3)、 的圆心为 (t , 0),半径为1.若 ( , ) ,直接写出t的取值范围.