广西壮族自治区桂林市2018年中考数学试卷
试卷更新日期:2018-07-12 类型:中考真卷
一、选择题:
-
1. 2018的相反数是( )A、 2018 B、-2018 C、 D、2. 下列图形是轴对称图形的是( )A、
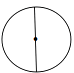 B、
B、 C、
C、 D、
D、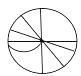 3. 如图,直线a,b被直线c所截,a//b,∠1=60°,则∠2的度数是( )
3. 如图,直线a,b被直线c所截,a//b,∠1=60°,则∠2的度数是( )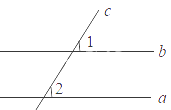 A、120° B、60° C、45° D、30°4. 如图所示的几何体的主视图是( )
A、120° B、60° C、45° D、30°4. 如图所示的几何体的主视图是( )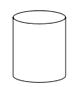 A、
A、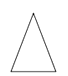 B、
B、 C、
C、 D、
D、 5. 用代数式表示:a的2倍与3 的和,下列表示正确的是( )A、2a-3 B、2a+3 C、2(a-3) D、2(a+3)6. 2018年5月3日,中国科学院在上海发布了中国首款人工智能芯片:寒武纪(MLU100),该芯片在平衡模式下的等效理论峰值速度达每秒128 000 000 000 000次定点运算,将数
5. 用代数式表示:a的2倍与3 的和,下列表示正确的是( )A、2a-3 B、2a+3 C、2(a-3) D、2(a+3)6. 2018年5月3日,中国科学院在上海发布了中国首款人工智能芯片:寒武纪(MLU100),该芯片在平衡模式下的等效理论峰值速度达每秒128 000 000 000 000次定点运算,将数128 000 000 000 000用科学记数法表示为( )
A、 1.28 1014 B、1.28 10-14 C、128 1012 D、0.128 10117. 下列计算正确的是( )A、 B、 C、 D、8. 一组数据:5,7,10,5,7,5,6,这组数据的众数和中位数分别是( )A、10和7 B、5和7 C、6和7 D、5和69. 已知关于x的一元二次方程 有两个相等的实根,则k的值为( )A、 B、 C、2或3 D、 或10. 若 ,则x,y的值为( )A、 B、 C、 D、11. 如图,在正方形ABCD中,AB=3,点M在CD的边上,且DM=1,ΔAEM与ΔADM关于AM所在的直线对称,将ΔADM按顺时针方向绕点A旋转90°得到ΔABF,连接EF,则线段EF的长为( )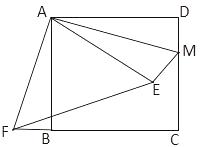 A、3 B、 C、 D、12. 如图,在平面直角坐标系中,M、N、C三点的坐标分别为( ,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作 交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
A、3 B、 C、 D、12. 如图,在平面直角坐标系中,M、N、C三点的坐标分别为( ,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作 交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:
-
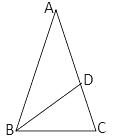
13. 比较大小:-30.(填“< ”,“=”,“ > ”)14. 因式分解:x2-4=15. 某学习小组共有学生5人,在一次数学测验中,有2人得85分,2人得90分,1人得70分,该学习小组的平均分为分.16. 如图,在ΔABC中,∠A=36°,AB=AC,BD平分∠ABC,则图中等腰三角形的个数是
 17. 如图,矩形OABC的边AB与x轴交于点D,与反比例函数 (k>0)在第一象限的图像交于点E,∠AOD=30°,点E的纵坐标为1,ΔODE的面积是 ,则k的值是
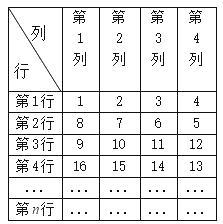
17. 如图,矩形OABC的边AB与x轴交于点D,与反比例函数 (k>0)在第一象限的图像交于点E,∠AOD=30°,点E的纵坐标为1,ΔODE的面积是 ,则k的值是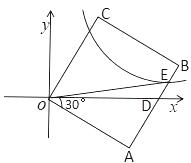 18. 将从1开始的连续自然数按右图规律排列:
18. 将从1开始的连续自然数按右图规律排列:规定位于第m行,第n列的自然数10记为(3,2),自然数15记为(4,2)......按此规律,自然数2018记为
三、解答题:
-
19. 计算:20. 解不等式 ,并把它的解集在数轴上表示出来.21. 如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
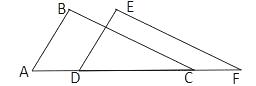 (1)、求证:ΔABC≌DEF;(2)、若∠A=55°,∠B=88°,求∠F的度数.22. 某校为了解高一年级住校生在校期间的月生活支出情况,从高一年级600名住校学生中随机抽取部分学生,对他们今年4月份的生活支出情况进行调查统计,并绘制成如下统计图表:
(1)、求证:ΔABC≌DEF;(2)、若∠A=55°,∠B=88°,求∠F的度数.22. 某校为了解高一年级住校生在校期间的月生活支出情况,从高一年级600名住校学生中随机抽取部分学生,对他们今年4月份的生活支出情况进行调查统计,并绘制成如下统计图表:组别 月生活支出x(单位:元) 频数(人数) 频率 第一组 x<300 4 0.10 第二组 300≤x≤350 2 0.05 第三组 350≤x≤400 16 n 第四组 400≤x≤450 m 0.30 第五组 450≤x≤500 4 0.10 第六组 x≥500 2 0.05 请根据图表中所给的信息,解答下列问题:
(1)、在这次调查中共随机抽取了名学生,图表中的m= , n=;(2)、请估计该校高一年级600名住校学生今年4月份生活支出低于350元的学生人数;(3)、现有一些爱心人士有意愿资助该校家庭困难的学生,学校在本次调查的基础上,经过进一步核实,确认高一(2)班有A,B,C三名学生家庭困难,其中A,B为女生,C为男生. 李阿姨申请资助他们中的两名,于是学校让李阿姨从A,B,C三名学生中依次随机抽取两名学生进行资助,请用列表法(或树状图法)求恰好抽到A,B两名女生的概率.23. 如图所示,在某海域,一般指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A的救援?(参考数据: , , 结果精确到0.1小时)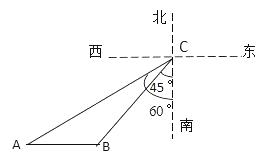 24. 某校利用暑假进行田径场的改造维修,项目承包单位派遣一号施工队进场施工,计划用40天时间完成整个工程:当一号施工队工作5天后,承包单位接到通知,有一大型活动要在该田径场举行,要求比原计划提前14天完成整个工程,于是承包单位派遣二号与一号施工队共同完成剩余工程,结果按通知要求如期完成整个工程.(1)、若二号施工队单独施工,完成整个工程需要多少天?(2)、若此项工程一号、二号施工队同时进场施工,完成整个工程需要多少天?25. 如图1,已知⊙O是ΔADB的外接圆,∠ADB的平分线DC交AB于点M,交⊙O于点C,连接AC,BC.
24. 某校利用暑假进行田径场的改造维修,项目承包单位派遣一号施工队进场施工,计划用40天时间完成整个工程:当一号施工队工作5天后,承包单位接到通知,有一大型活动要在该田径场举行,要求比原计划提前14天完成整个工程,于是承包单位派遣二号与一号施工队共同完成剩余工程,结果按通知要求如期完成整个工程.(1)、若二号施工队单独施工,完成整个工程需要多少天?(2)、若此项工程一号、二号施工队同时进场施工,完成整个工程需要多少天?25. 如图1,已知⊙O是ΔADB的外接圆,∠ADB的平分线DC交AB于点M,交⊙O于点C,连接AC,BC.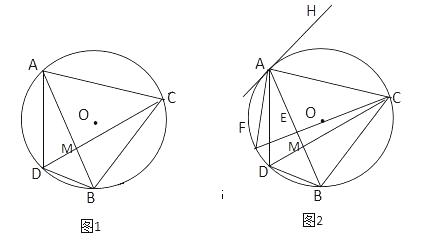 (1)、求证:AC=BC;(2)、如图2,在图1 的基础上做⊙O的直径CF交AB于点E,连接AF,过点A作⊙O的切线AH,若AH//BC,求∠ACF的度数;(3)、在(2)的条件下,若ΔABD的面积为 ,ΔABD与ΔABC的面积比为2:9,求CD的长.26. 如图,已知抛物线y=ax2+bx+6(a≠0)与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.
(1)、求证:AC=BC;(2)、如图2,在图1 的基础上做⊙O的直径CF交AB于点E,连接AF,过点A作⊙O的切线AH,若AH//BC,求∠ACF的度数;(3)、在(2)的条件下,若ΔABD的面积为 ,ΔABD与ΔABC的面积比为2:9,求CD的长.26. 如图,已知抛物线y=ax2+bx+6(a≠0)与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.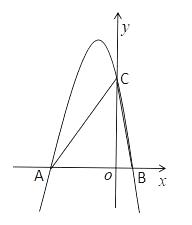 (1)、求抛物线y的函数表达式及点C的坐标;(2)、点M为坐标平面内一点,若MA=MB=MC,求点M的坐标;(3)、在抛物线上是否存在点E,使4tan∠ABE=11tan∠ACB?若存在,求出满足条件的所有点E的坐标;若不存在,请说明理由.
(1)、求抛物线y的函数表达式及点C的坐标;(2)、点M为坐标平面内一点,若MA=MB=MC,求点M的坐标;(3)、在抛物线上是否存在点E,使4tan∠ABE=11tan∠ACB?若存在,求出满足条件的所有点E的坐标;若不存在,请说明理由.