广东省2018年中考数学试卷
试卷更新日期:2018-07-12 类型:中考真卷
一、选择题
-
1. 四个实数0、 、﹣3.14、2中,最小的数是( )A、0 B、 C、﹣3.14 D、22. 据有关部门统计,2018年“五一小长假”期间,广东各大景点共接待游客约14420000人次,将数14420000用科学记数法表示为( )A、1.442×107 B、0.1442×107 C、1.442×108 D、0.1442×1083. 如图,由5个相同正方体组合而成的几何体,它的主视图是( )
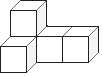 A、
A、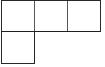 B、
B、 C、
C、 D、
D、 4. 数据1、5、7、4、8的中位数是( )A、4 B、5 C、6 D、75. 下列所述图形中,是轴对称图形但不是中心对称图形的是( )A、圆 B、菱形 C、平行四边形 D、等腰三角形6. 不等式3x﹣1≥x+3的解集是( )A、x≤4 B、x≥4 C、x≤2 D、x≥27. 在△ABC中,点D,E分别为边AB,AC的中点,则△ADE与△ABC的面积之比为( )A、 B、 C、 D、8. 如图,AB∥CD,且∠DEC=100°,∠C=40°,则∠B的大小是( )
4. 数据1、5、7、4、8的中位数是( )A、4 B、5 C、6 D、75. 下列所述图形中,是轴对称图形但不是中心对称图形的是( )A、圆 B、菱形 C、平行四边形 D、等腰三角形6. 不等式3x﹣1≥x+3的解集是( )A、x≤4 B、x≥4 C、x≤2 D、x≥27. 在△ABC中,点D,E分别为边AB,AC的中点,则△ADE与△ABC的面积之比为( )A、 B、 C、 D、8. 如图,AB∥CD,且∠DEC=100°,∠C=40°,则∠B的大小是( )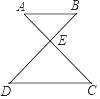 A、30° B、40° C、50° D、60°9. 关于x的一元二次方程x2﹣3x+m=0有两个不相等的实数根,则实数m的取值范围是( )A、m< B、m≤ C、m> D、m≥10. 如图,点P是菱形ABCD边上的一动点,它从点A出发沿在A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )
A、30° B、40° C、50° D、60°9. 关于x的一元二次方程x2﹣3x+m=0有两个不相等的实数根,则实数m的取值范围是( )A、m< B、m≤ C、m> D、m≥10. 如图,点P是菱形ABCD边上的一动点,它从点A出发沿在A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )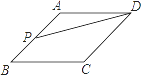 A、
A、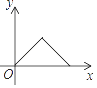 B、
B、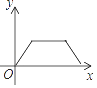 C、
C、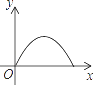 D、
D、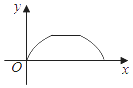
二、填空题
-
11. 同圆中,已知弧AB所对的圆心角是100°,则弧AB所对的圆周角是 .12. 分解因式:x2﹣2x+1= .13. 一个正数的平方根分别是x+1和x﹣5,则x= .14. 已知 +|b﹣1|=0,则a+1= .15. 如图,矩形ABCD中,BC=4,CD=2,以AD为直径的半圆O与BC相切于点E,连接BD,则阴影部分的面积为 . (结果保留π)
 16. 如图,已知等边△OA1B1 , 顶点A1在双曲线y= (x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2 , 过A2作A2B2∥A1B1交x轴于点B2 , 得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3 , 过A3作A3B3∥A2B2交x轴于点B3 , 得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为 .
16. 如图,已知等边△OA1B1 , 顶点A1在双曲线y= (x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2 , 过A2作A2B2∥A1B1交x轴于点B2 , 得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3 , 过A3作A3B3∥A2B2交x轴于点B3 , 得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为 .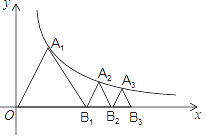
三、解答题
-
17. 计算:|﹣2|﹣20180+( )﹣118. 先化简,再求值: • ,其中a= .19. 如图,BD是菱形ABCD的对角线,∠CBD=75°,
 (1)、请用尺规作图法,作AB的垂直平分线EF,垂足为E,交AD于F;(不要求写作法,保留作图痕迹)(2)、在(1)条件下,连接BF,求∠DBF的度数.20. 某公司购买了一批A、B型芯片,其中A型芯片的单价比B型芯片的单价少9元,已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等.
(1)、请用尺规作图法,作AB的垂直平分线EF,垂足为E,交AD于F;(不要求写作法,保留作图痕迹)(2)、在(1)条件下,连接BF,求∠DBF的度数.20. 某公司购买了一批A、B型芯片,其中A型芯片的单价比B型芯片的单价少9元,已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等.
(1)、求该公司购买的A、B型芯片的单价各是多少元?(2)、若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条A型芯片?21. 某企业工会开展“一周工作量完成情况”调查活动,随机调查了部分员工一周的工作量剩余情况,并将调查结果统计后绘制成如图1和图2所示的不完整统计图. (1)、被调查员工人数为人:(2)、把条形统计图补充完整;(3)、若该企业有员工10000人,请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人?
(1)、被调查员工人数为人:(2)、把条形统计图补充完整;(3)、若该企业有员工10000人,请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人?
22. 如图,矩形ABCD中,AB>AD,把矩形沿对角线AC所在直线折叠,使点B落在点E处,AE交CD于点F,连接DE. (1)、求证:△ADE≌△CED;(2)、求证:△DEF是等腰三角形.23. 如图,已知顶点为C(0,﹣3)的抛物线y=ax2+b(a≠0)与x轴交于A,B两点,直线y=x+m过顶点C和点B.
(1)、求证:△ADE≌△CED;(2)、求证:△DEF是等腰三角形.23. 如图,已知顶点为C(0,﹣3)的抛物线y=ax2+b(a≠0)与x轴交于A,B两点,直线y=x+m过顶点C和点B. (1)、求m的值;(2)、求函数y=ax2+b(a≠0)的解析式;(3)、抛物线上是否存在点M,使得∠MCB=15°?若存在,求出点M的坐标;若不存在,请说明理由.24. 如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.
(1)、求m的值;(2)、求函数y=ax2+b(a≠0)的解析式;(3)、抛物线上是否存在点M,使得∠MCB=15°?若存在,求出点M的坐标;若不存在,请说明理由.24. 如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.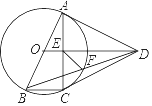 (1)、证明:OD∥BC;(2)、若tan∠ABC=2,证明:DA与⊙O相切;
(1)、证明:OD∥BC;(2)、若tan∠ABC=2,证明:DA与⊙O相切;
(3)、在(2)条件下,连接BD交于⊙O于点F,连接EF,若BC=1,求EF的长.25. 已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O顺时针旋转60°,如题图1,连接BC. (1)、填空:∠OBC=°;(2)、如图1,连接AC,作OP⊥AC,垂足为P,求OP的长度;(3)、如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN的面积为y,求当x为何值时y取得最大值?最大值为多少?
(1)、填空:∠OBC=°;(2)、如图1,连接AC,作OP⊥AC,垂足为P,求OP的长度;(3)、如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN的面积为y,求当x为何值时y取得最大值?最大值为多少?