2018年高考数学真题分类汇编专题20：导数在函数中的应用（综合题）

试卷更新日期：2018-07-11 类型：二轮复习

进入出卷网下载

一、导数在函数中的应用

1. 已知函数 $f (x) = \frac{1}{x} - x + a \ln x$

(1)、讨论 $f (x)$ 的单调性；

(2)、若 $f (x)$ 存在两个极值点 $x_{1} ， x_{2}$ ，证明： $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} < a - 2$

查看试题解析
2. 已知函数f(x)=ae^x-lnx-1

(1)、设x=2是f(x)的极值点，求a，并求f(x)的单调区间

(2)、证明：当a≥ $\frac{1}{e}$ 时，f(x)≥0

查看试题解析
3. 已知函数 $f (x) = e^{x} - a x^{2}$

(1)、若a=1，证明：当 $x \geq 0$ 时， $f (x) \geq 1 ；$

(2)、若 $f (x)$ 在 $(0 ， + \infty)$ 只有一个零点，求 $a$ .

查看试题解析
4. 已知函数 $f (x) = \frac{1}{3} x^{3} - a (x^{2} + x + 1)$

(1)、若a=3，求 $f (x)$ 的单调区间

(2)、证明： $f (x)$ 只有一个零点

查看试题解析
5. 已知函数 $f (x) = \frac{a x^{2} + x - 1}{e^{x}}$

(1)、求函数 $y = f (x)$ 在点 $(0 ， - 1)$ 处的切线方程

(2)、证明：当 $a \geq 1$ 时， $f (x) + e \geq 0$

查看试题解析
6. 已知函数 $f (x) = (2 + x + a x^{2}) \ln (1 + x) - 2 x$ ．

(1)、若 $a = 0$ ，证明：当 $- 1 < x < 0$ 时， $f (x) < 0$ ；当 $x > 0$ 时， $f (x) > 0$ ；

(2)、若 $x = 0$ 是 $f (x)$ 的极大值点，求a．

查看试题解析
7. 设函数 $f (x)$ =[ $a x^{2}$ -(4a+1)x+4a+3] $e^{x}$ .
（I）若曲线y= f（x）在点(1， $f (1)$ )处的切线与X轴平行，求a：
(II)若 $f (x)$ 在x=2处取得极小值，求a的取值范围。

查看试题解析
8. 设函数 $f (x) = [a x^{2} - (3 a + 1) x + 3 a + 2] e^{x}$ .
（Ⅰ）若曲线 $y = f (x)$ 在点 $(2 ， f (2))$ 处的切线斜率为0，求a；
（Ⅱ）若 $f (x)$ 在 $x = 1$ 处取得极小值，求a的取值范围.

查看试题解析
9. 已知函数 $f (x) = a^{x}$ ， $g (x) = \log_{a} x$ ，其中a>1.
（Ⅰ）求函数 $h (x) = f (x) - x \ln a$ 的单调区间；
（Ⅱ）若曲线 $y = f (x)$ 在点 $(x_{1} ， f (x_{1}))$ 处的切线与曲线 $y = g (x)$ 在点 $(x_{2} ， g (x_{2}))$ 处的切线平行，证明 $x_{1} + g (x_{2}) = - \frac{2 \ln \ln a}{\ln a}$ ；
（Ⅲ）证明当 $a \geq e^{\frac{1}{e}}$ 时，存在直线l ，使l是曲线 $y = f (x)$ 的切线，也是曲线 $y = g (x)$ 的切线.

查看试题解析
10. 已知函数f(x)= $\sqrt{x}$ −lnx ．
（Ⅰ）若f(x)在x=x₁ ， x₂(x₁≠x₂)处导数相等，证明：f(x₁)+f(x₂)>8−8ln2；
（Ⅱ）若a≤3−4ln2，证明：对于任意k>0，直线y=kx+a与曲线y=f(x)有唯一公共点．

查看试题解析
11. 某农场有一块农田，如图所示，它的边界由圆 $O$ 的一段圆弧 $M P N$ ( $P$ 为此圆弧的中点)和线段 $M N$ 构成，已知圆 $O$ 的半径为40米，点 $P$ 到 $M N$ 的距离为50米，先规划在此农田上修建两个温室大棚，大棚Ⅰ内的地块形状为矩形 $A B C D$ .大棚Ⅱ内的地块形状为 $Δ C D P$ 要求 $A B$ 均在线段 $M N$ 上， $C ， D$ 均在圆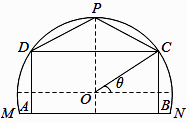弧上，设 $O C$ 与 $M N$ 所成的角为θ

(1)、用 $θ$ 分别表示矩形 $A B C D$ 和 $Δ C D P$ 的面积，并确定 $\sin θ$ 的取值范围

(2)、若大棚Ⅰ内种植甲种蔬菜，大棚Ⅱ内种植乙种蔬菜，且甲、乙两种蔬菜的单位面积年产值之比为4：3.求当 $θ$ 为何值时，能使甲、乙两种蔬菜的年总产值最大.

查看试题解析
12. 记 $f^{'} (x) ， g^{'} (x)$ 分别为函数 $f (x) ， g (x)$ 的导函数.若存在 $x_{0} \in R$ ，满足 $f (x_{0}) = g (x_{0})$ 且 $f^{'} (x_{0}) = g^{'} (x_{0})$ ，则称 $x_{0}$ 为函数 $f (x)$ 与 $g (x)$ 的一个“S点”.

(1)、证明：函数 $f (x) = x$ 与 $g (x) = x^{2} + 2 x - 2$ 不存在“S点”.

(2)、若函数 $f (x) = a x^{2} - 1$ 与 $g (x) = \ln x$ 存在“S点”，求实数 $a$ 的值.

(3)、已知函数 $f (x) = - x^{2} + a$ ， $g (x) = \frac{b e^{x}}{x}$ ，对任意 $a > 0$ ，判断是否存在 $b > 0$ ，使函数 $f (x)$ 与 $g (x)$ 在区间 $(0 ， + \infty)$ 内存在”S点”，并说明理由.

查看试题解析