2018年高考数学真题分类汇编专题16：概率与统计（综合题）-在线组卷题库

1. 某工厂的某种产品成箱包装，每箱200件，每一箱产品在交付用户之前要对产品作检验，如检验出不合格品，则更换为合格品，检验时，先从这箱产品中任取20件作检验，再根据检验结果决定是否对余下的所有产品作检验。设每件产品为不合格的概率为品p（

0 < p < 1

），且各件产品是否为不合格品相互独立。

(1)、记20件产品中恰有2件不合格品的概率为

f (p)

，求

f (p)

的最大值点

p_{0}

(2)、现对一箱产品检验了20件，结果恰有2件不合格品，以（1）中确定的

p_{0}

作为

p

的值。已知每件产品的检验费用为2元，若有不合格品进入用户手中，则工厂要对每件不合格品支付25元的赔偿费用

(i)若不对该箱余下的产品作检验，这一箱的检验费用与赔偿费用的和记为 $X$ ，求 $E X$ ；

(ii)以检验费用与赔偿费用和的期望值为决策依据，是否该对这箱余下的所有产品作检验？

查看试题解析

2. 某家庭记录了未使用节水龙头50天的日用水量数据(单位：m3)和使用了节水龙头50天的日用水量数据，得到频数分布表如下：

未使用节水龙头50天的日用水量频数分布表

日用水量	[0，0.1）	[0.1，0.2）	[0.2，0.3	[0.3，0.4）	[0.4，0.5）	[0.5，0.6）	[0.6，0.7）
频数	1	3	2	4	9	26	5

使用节水龙头50天的日用水量频数分布表

日用水量	[0，0.1）	[0.1，0.2）	[0.2，0.3）	[0.3，0.4）	[0.4，0.5）	[0.5，0.6）
频数	1	5	13	10	16	5

(1)、在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图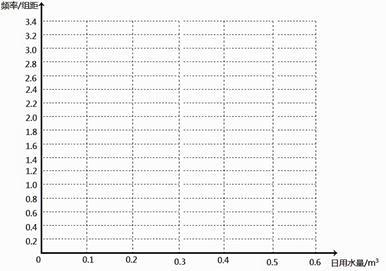

(2)、估计该家庭使用节水龙头后，日用水量小于0.35m³的概率

(3)、估计该家庭使用节水龙头后，一年能节省多少水?(一年按365天计算，同一组中的数据以这组数据所在区间中点的值作代表)

查看试题解析

3. 下图是某地区2000年至2016年环境基础设施投资额

y

(单位：亿元)的折线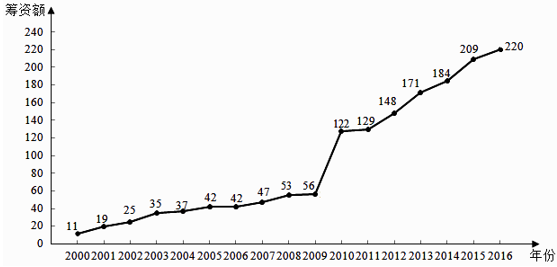图。

为了预测该地区2018年的环境基础设施投资额，建立了 $y$ 与时间变量t的两个线性回归模型，根据2000年至2016年的数据（时间变量 $t$ 的值依次为1，2，…，17）建立模型①： $\overset{\land}{y}$ =-30.4+13.5t .根据2010年至2016年的数据（时间变量t的值依次为1，2，…，7）建立模型 ②： $\hat{y} = 99 + 17.5 t$

(1)、分别利用这两个模型，求该地区2018年的环境基础设施投资的预测值；

(2)、你认为用哪个模型得到的预测值更可靠？并说明理由。

查看试题解析

4. 某工厂为提高生产效率，开展技术创新活动，提出了完成某项项目生产任务的两种新的生产方式，为比较两种生产方式的效率，选取40名工人，将他们随即分成两组，每组20人，第一组工人用第一种生产方式，第二组工人用第二种生产方式，根据工人完成生产任务的工作时间(单位：min)绘制了如下茎叶图：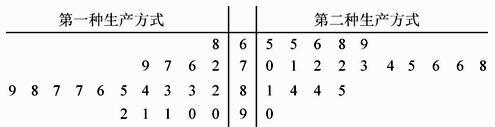

(1)、根据茎叶图判断哪种生产方式的效率更高？并说明理由；

(2)、求40名工人完成生产任务所需时间的中位数m，并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表：

	超过m	不超过m
第一种生产方式
第二种生产方式

(3)、根据2中的列联表，能否有99%的把握认为两种生产方式的效率有差异？

附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，

查看试题解析

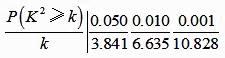5. 电影公司随机收集了电影的有关数据，经分类整理得到下表：

电影类型	第一类	第二类	第三类	第四类	第五类	第六类
电影部数	140	50	300	200	800	510
好评率	0.4	0.2	0.15	0.25	0.2	0.1

好评率是指：一类电影中获得好评的部数与该类电影的部数的比值.

（Ⅰ）从电影公司收集的电影中随机选取1部，求这部电影是获得好评的第四类电影的概率；

（Ⅱ）随机选取1部电影，估计这部电影没有获得好评的概率；

（Ⅲ）电影公司为增加投资回报，拟改变投资策略，这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化，那么哪类电影的好评率增加0.1，哪类电影的好评率减少0.1，使得获得好评的电影总部数与样本中的电影总部数的比值达到最大？（只需写出结论）

查看试题解析

6. 电影公司随机收集了电影的有关数据，经分类整理得到下表：

电影类型	第一类	第二类	第三类	第四类	第五类	第六类
电影部数	140	50	300	200	800	510
好评率	0.4	0.2	0.15	0.25	0.2	0.1

好评率是指：一类电影中获得好评的部数与该类电影的部数的比值

假设所有电影是否获得好评相互独立。

（Ⅰ）从电影公司收集的电影中随机选取1部，求这部电影是获得好评的第四类电影的概率；

（Ⅱ）从第四类电影和第五类电影中各随机选取1部，估计恰有1部获得好评的概率；

（Ⅲ）假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等，用“ $ξ_{k} = 1$ ”表示第k类电影得到人们喜欢，“ $ξ_{k} = 0$ ”表示第k类电影没有得到人们喜欢（k=1，2，3，4，5，6），写出方差 $D ξ_{1} ， D ξ_{2} ， D ξ_{3} ， D ξ_{4} ， D ξ_{5} ， D ξ_{6}$ 的大小关系。

查看试题解析

7. 已知某校甲、乙、丙三个年级的学生志愿者人数分别为240，160，160．现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动．

（Ⅰ）应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人？

（Ⅱ）设抽出的7名同学分别用A ， B ， C ， D ， E ， F ， G表示，现从中随机抽取2名同学承担敬老院的卫生工作．

（i）试用所给字母列举出所有可能的抽取结果；

（ii）设M为事件“抽取的2名同学来自同一年级”，求事件M发生的概率．

查看试题解析

8. 已知某单位甲、乙、丙三个部门的员工人数分别为24，16，16.现采用分层抽样的方法从中抽取7人，进行睡眠时间的调查.

（Ⅰ）应从甲、乙、丙三个部门的员工中分别抽取多少人？

（Ⅱ）若抽出的7人中有4人睡眠不足，3人睡眠充足，现从这7人中随机抽取3人做进一步的身体检查.

（i）用X表示抽取的3人中睡眠不足的员工人数，求随机变量X的分布列与数学期望；

（ii）设A为事件“抽取的3人中，既有睡眠充足的员工，也有睡眠不足的员工”，求事件A发生的概率.

查看试题解析

2018年高考数学真题分类汇编专题16：概率与统计（综合题）

一、概率与统计