2018年高考数学真题分类汇编专题11：空间几何体（基础题）

试卷更新日期：2018-07-11 类型：二轮复习

进入出卷网下载

一、空间几何体

1. 某圆柱的高为2，底面周长为16，其三视图如右图。圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为（）

A、 $2 \sqrt{17}$ B、 $2 \sqrt{5}$ C、 $3$ D、2

查看试题解析
2. 已知圆柱的上、下底面的中心分别为O₁ ， O₂ ，过直线O₁O₂的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为（）

A、 $12 \sqrt{2} π$ B、12π C、 $8 \sqrt{2} π$ D、 $10 π$

查看试题解析
3. 已知正方体的棱长为1，每条棱所在直线与平面 $α$ 所成的角都相等，则 $α$ 截此正方体所得截面面积的最大值为（）

A、 $\frac{3 \sqrt{3}}{4}$ B、 $\frac{2 \sqrt{3}}{3}$ C、 $\frac{3 \sqrt{2}}{4}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
4. 在长方体ABCD-A₁B₁C₁D₁中，AB=BC=2，AC₁与平面BB₁CC₁所成的角为30°，则该长方体的体积为（）

A、8 B、6 $\sqrt{2}$ C、8 $\sqrt{2}$ D、8 $\sqrt{3}$

查看试题解析
5. 在长方形ABCD-A₁B₁C₁D₁中，AB=BC=1，AA₁= $\sqrt{3}$ ，则异面直线AD₁与DB₁所成角的余弦值为（）

A、 $\frac{1}{5}$ B、 $\frac{\sqrt{5}}{6}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
6. 在正方体ABCD-A₁B₁C₁D₁中，E为棱CC₁的重点，则异面直线AE与CD所成角的正切值为（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{5}}{2}$ D、 $\frac{\sqrt{7}}{2}$

查看试题解析
7. 设 $A ， B ， C ， D$ 是同一个半径为 $4$ 的球的球面上四点， $Δ A B C$ 为等边三角形且其面积为 $9 \sqrt{3}$ ，则三棱锥 $D - A B C$ 体积的最大值为（）

A、 $12 \sqrt{3}$ B、 $18 \sqrt{3}$ C、 $24 \sqrt{3}$ D、 $54 \sqrt{3}$

查看试题解析
8. 中国古建筑借助榫卯将木构件连接起来，构建的突出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头，若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（）

A、 B、 C、 D、

查看试题解析
9. 某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（）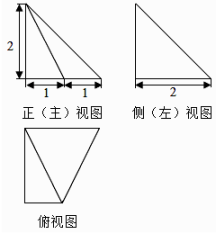

A、1 B、2 C、3 D、4

查看试题解析
10. 《九章算术》中，称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设AA₁是正六棱柱的一条侧棱，如图，若阳马以该正六棱柱的顶点为顶点，以AA₁为底面矩形的一边，则这样的阳马的个数是（）

A、4 B、8 C、12 D、16

查看试题解析
11. 某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm³）是（）

A、2 B、4 C、6 D、8

查看试题解析
12. 已知四棱锥S−ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点（不含端点），设SE与BC所成的角为θ₁ ， SE与平面ABCD所成的角为θ₂ ，二面角S−AB−C的平面角为θ₃ ，则（）

A、θ₁≤θ₂≤θ₃ B、θ₃≤θ₂≤θ₁ C、θ₁≤θ₃≤θ₂ D、θ₂≤θ₃≤θ₁

查看试题解析
13. 已知圆锥的顶点为S，母线SA，SB所成角的余弦值为 $\frac{7}{8}$ ，SA与圆锥底面所成角为45°。若△SAB的面积为 $5 \sqrt{15}$ ，则圆锥的侧面积为。

查看试题解析
14. 已知圆锥的顶点为S，母线SA，SB互相垂直，SA与圆锥底面所成角为30°，若 $△ S A B$ 的面积为8，则该圆锥的体积为

查看试题解析
15. 已知向量 $\vec{a} = (1 ， 2)$ ， $\vec{b} = (2 ， - 2)$ ， $\vec{c} = (1 ， λ)$ ，若 $\vec{c} ∥ (2 \vec{a} + \vec{b})$ ，则 $λ =$ 。

查看试题解析
16. 如图，已知正方体ABCD–A₁B₁C₁D₁的棱长为1，则四棱柱A₁–BB₁D₁D的体积为．

查看试题解析
17. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为1，除面 $A B C D$ 外，该正方体其余各面的中心分别为点E ， F ， G ， H ， M(如图)，则四棱锥 $M - E F G H$ 的体积为

查看试题解析
18. 如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为

查看试题解析