浙江省台州市2018年中考数学试卷
试卷更新日期:2018-07-10 类型:中考真卷
一、选择题
-
1. 比-1小2的数是( )A、3 B、1 C、-2 D、-32. 在下列四个新能源汽车车标的设计图中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 计算 ,结果正确的是( )A、1 B、 C、 D、4. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间5. 某篮球运动员在连续7场比赛中的得分(单位:分)依次为20,18,23,17,20,20,18,则这组数据的众数与中位数分别是( )A、18分,17分 B、20分,17分 C、20分,19分 D、20分,20分6. 下列命题正确的是( )A、对角线相等的四边形是平行四边形 B、对角线相等的四边形是矩形 C、对角线互相垂直的平行四边形是菱形 D、对角线互相垂直且相等的四边形是正方形7. 正十边形的每一个内角的度数为( )A、 B、 C、 D、8. 如图,在 中, , .以点 为圆心,适当长为半径画弧,交 于点 ,交 于点 ,再分别以点 , 为圆心,大于 的长为半径画弧,两弧相交于点 ,射线 交 的延长线于点 ,则 的长是( )
3. 计算 ,结果正确的是( )A、1 B、 C、 D、4. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间5. 某篮球运动员在连续7场比赛中的得分(单位:分)依次为20,18,23,17,20,20,18,则这组数据的众数与中位数分别是( )A、18分,17分 B、20分,17分 C、20分,19分 D、20分,20分6. 下列命题正确的是( )A、对角线相等的四边形是平行四边形 B、对角线相等的四边形是矩形 C、对角线互相垂直的平行四边形是菱形 D、对角线互相垂直且相等的四边形是正方形7. 正十边形的每一个内角的度数为( )A、 B、 C、 D、8. 如图,在 中, , .以点 为圆心,适当长为半径画弧,交 于点 ,交 于点 ,再分别以点 , 为圆心,大于 的长为半径画弧,两弧相交于点 ,射线 交 的延长线于点 ,则 的长是( )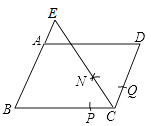 A、 B、1 C、 D、9. 甲、乙两运动员在长为 的直道 ( , 为直道两端点)上进行匀速往返跑训练,两人同时从 点起跑,到达 点后,立即转身跑向 点,到达 点后,又立即转身跑向 点……若甲跑步的速度为 ,乙跑步的速度为 ,则起跑后 内,两人相遇的次数为( )A、5 B、4 C、3 D、210. 如图,等边三角形 边长是定值,点 是它的外心,过点 任意作一条直线分别交 , 于点 , ,将 沿直线 折叠,得到 ,若 , 分别交 于点 , ,连接 , ,则下列判断错误的是( )
A、 B、1 C、 D、9. 甲、乙两运动员在长为 的直道 ( , 为直道两端点)上进行匀速往返跑训练,两人同时从 点起跑,到达 点后,立即转身跑向 点,到达 点后,又立即转身跑向 点……若甲跑步的速度为 ,乙跑步的速度为 ,则起跑后 内,两人相遇的次数为( )A、5 B、4 C、3 D、210. 如图,等边三角形 边长是定值,点 是它的外心,过点 任意作一条直线分别交 , 于点 , ,将 沿直线 折叠,得到 ,若 , 分别交 于点 , ,连接 , ,则下列判断错误的是( )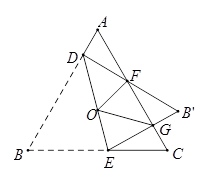 A、 B、 的周长是一个定值 C、四边形 的面积是一个定值 D、四边形 的面积是一个定值
A、 B、 的周长是一个定值 C、四边形 的面积是一个定值 D、四边形 的面积是一个定值二、填空题
-
11. 若分式 有意义,则实数 的取值范围是 .12. 已知关于 的一元二次方程 有两个相等的实数根,则 .13. 一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.随机摸出一个小球然后放回,再随机摸出一个小球,则两次摸出的小球标号相同的概率是 .14. 如图, 是 的直径, 是 上的点,过点 作 的切线交 的延长线于点 .若∠A=32°,则 度.
 15. 如图,把平面内一条数轴 绕原点 逆时针旋转角 得到另一条数轴 , 轴和 轴构成一个平面斜坐标系.规定:过点 作 轴的平行线,交 轴于点 ,过点 在 轴的平行线,交 轴于点 ,若点 在 轴上对应的实数为 ,点 在 轴上对应的实数为 ,则称有序实数对 为点 的斜坐标.在某平面斜坐标系中,已知θ=60°,点 的斜坐标为 ,点 与点 关于 轴对称,则点 的斜坐标为 .
15. 如图,把平面内一条数轴 绕原点 逆时针旋转角 得到另一条数轴 , 轴和 轴构成一个平面斜坐标系.规定:过点 作 轴的平行线,交 轴于点 ,过点 在 轴的平行线,交 轴于点 ,若点 在 轴上对应的实数为 ,点 在 轴上对应的实数为 ,则称有序实数对 为点 的斜坐标.在某平面斜坐标系中,已知θ=60°,点 的斜坐标为 ,点 与点 关于 轴对称,则点 的斜坐标为 .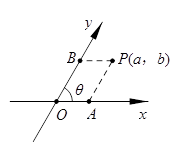 16. 如图,在正方形 中, ,点 , 分别在 , 上, , , 相交于点 .若图中阴影部分的面积与正方形 的面积之比为 ,则 的周长为 .
16. 如图,在正方形 中, ,点 , 分别在 , 上, , , 相交于点 .若图中阴影部分的面积与正方形 的面积之比为 ,则 的周长为 .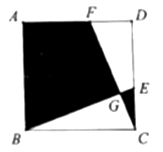
三、解答题
-
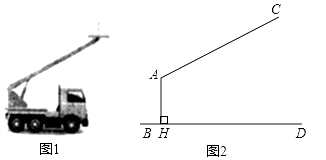
17. 计算: .18. 解不等式组: .19. 图1是一辆吊车的实物图,图2是其工作示意图, 是可以伸缩的起重臂,其转动点 离地面 的高度 为 .当起重臂 长度为 ,张角 为 时,求操作平台 离地面的高度(结果保留小数点后一位;参考数据: , , ).
 20. 如图,函数 的图象与函数 的图象相交于点 .
20. 如图,函数 的图象与函数 的图象相交于点 .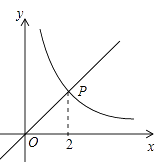 (1)、 求 , 的值;(2)、直线 与函数 的图象相交于点 ,与函数 的图象相交于点 ,求线段 长.21. 某市明年的初中毕业升学考试,拟将“引体向上”作为男生体育考试的一个必考项目,满分为10分.有关部分为提前了解明年参加初中毕业升学考试的男生的“引体向上”水平,在全市八年级男生中随机抽取了部分男生,对他们的“引体向上”水平进行测试,并将测试结果绘制成如下统计图表(部分信息未给出):
(1)、 求 , 的值;(2)、直线 与函数 的图象相交于点 ,与函数 的图象相交于点 ,求线段 长.21. 某市明年的初中毕业升学考试,拟将“引体向上”作为男生体育考试的一个必考项目,满分为10分.有关部分为提前了解明年参加初中毕业升学考试的男生的“引体向上”水平,在全市八年级男生中随机抽取了部分男生,对他们的“引体向上”水平进行测试,并将测试结果绘制成如下统计图表(部分信息未给出):抽取的男生“引体向上”成绩统计表
成绩
人数
0分
32
1分
30
2分
24
3分
11
4分
15
5分及以上
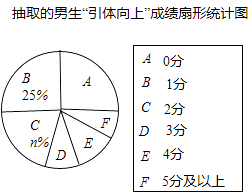
请你根据统计图表中的信息,解答下列问题:
(1)、 填空: , ;(2)、 求扇形统计图中 组的扇形圆心角的度数;(3)、目前该市八年级有男生3600名,请估计其中“引体向上”得零分的人数.22. 如图,在 中, , ,点 , 分别在 , 上,且 .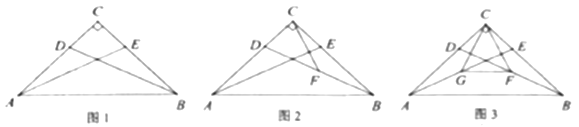 (1)、 如图1,求证: ;(2)、 如图2, 是 的中点.求证: ;(3)、 如图3, , 分别是 , 的中点.若 , ,求 的面积.23. 某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,并建立如下模型:设第 个月该原料药的月销售量为 (单位:吨), 与 之间存在如图所示的函数关系,其图象是函数 的图象与线段 的组合;设第 个月销售该原料药每吨的毛利润为 (单位:万元), 与 之间满足如下关系:
(1)、 如图1,求证: ;(2)、 如图2, 是 的中点.求证: ;(3)、 如图3, , 分别是 , 的中点.若 , ,求 的面积.23. 某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,并建立如下模型:设第 个月该原料药的月销售量为 (单位:吨), 与 之间存在如图所示的函数关系,其图象是函数 的图象与线段 的组合;设第 个月销售该原料药每吨的毛利润为 (单位:万元), 与 之间满足如下关系: (1)、 当 时,求 关于 的函数解析式;(2)、设第 个月销售该原料药的月毛利润为 (单位:万元).
(1)、 当 时,求 关于 的函数解析式;(2)、设第 个月销售该原料药的月毛利润为 (单位:万元).①求 关于 的函数解析式;
②该药厂销售部门分析认为, 是最有利于该原料药可持续生产和销售的月毛利润范围,求此范围所对应的月销售量 的最小值和最大值.
24. 如图, 是 的内接三角形,点 在 上,点 在弦 上( 不与 重合),且四边形 为菱形.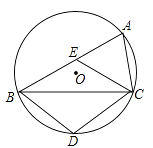 (1)、 求证: ;(2)、 求证: ;(3)、已知 的半径为3.
(1)、 求证: ;(2)、 求证: ;(3)、已知 的半径为3.①若 ,求 的长;
②当 为何值时, 的值最大?