江苏省徐州巿2018年中考数学试卷
试卷更新日期:2018-07-10 类型:中考真卷
一、选择题
-
1. 4的平方根是( )A、 B、2 C、-2 D、162. 一方有难、八方支援,截至5月26日12时,徐州巿累计为汶川地震灾区捐款约为11 180万元,该笔善款可用科学记数法表示为( )A、11.18×103万元 B、1.118×104万元 C、1.118×105万元 D、1.118×108万元3. 函数 中自变量x的取值范围是( )A、x≥-1 B、x≤-1 C、 x≠-1 D、 x=-14. 下列运算中,正确的是( )A、x3+x3=x6 B、x3·x9=x27 C、(x2)3=x5 D、x x2=x-15. 如果点(3,-4)在反比例函数 的图象上,那么下列各点中,在此图象上的是( )A、(3,4) B、 (-2,-6) C、(-2,6) D、(-3,-4)6. 下列平面展开图是由5个大小相同的正方形组成,其中沿正方形的边不能折成无盖小方盒的是( )A、
 B、
B、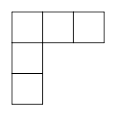 C、
C、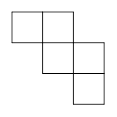 D、
D、 7. ⊙O1和⊙O2的半径分别为5和2,O1O2=3,则⊙O1和⊙O2的位置关系是( )A、内含 B、 内切 C、相交 D、外切8. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、正三角形 B、菱形 C、直角梯形 D、正六边形9. 下列事件中,必然事件是( )A、抛掷1个均匀的骰子,出现6点向上 B、两直线被第三条直线所截,同位角 C、366人中至少有2人的生日相同 D、实数的绝对值是非负数10. 如图,小明随意向水平放置的大正方形内部区域抛一个小球,则小球停在小正方形内部(阴影)区域的概率为( )
7. ⊙O1和⊙O2的半径分别为5和2,O1O2=3,则⊙O1和⊙O2的位置关系是( )A、内含 B、 内切 C、相交 D、外切8. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、正三角形 B、菱形 C、直角梯形 D、正六边形9. 下列事件中,必然事件是( )A、抛掷1个均匀的骰子,出现6点向上 B、两直线被第三条直线所截,同位角 C、366人中至少有2人的生日相同 D、实数的绝对值是非负数10. 如图,小明随意向水平放置的大正方形内部区域抛一个小球,则小球停在小正方形内部(阴影)区域的概率为( )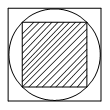 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
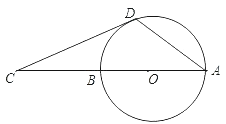
11. 因式分解:2x2-8=12. 徐州巿部分医保定点医院2018年第一季度的人均住院费用(单位:元)约为:12 320,11 880,10 370,8 570,10 640, 10240.这组数据的极差是元.13. 若 为方程 的两个实数根,则 .14. 边长为a的正三角形的面积等于.15. 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D.若,若∠C=18°,则∠CDA=.
 16. 如图,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE的周长等于cm.
16. 如图,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE的周长等于cm.
三、解答题
-
17. 计算: .18. 已知19. 解不等式组 ,并写出它的所有整数解.20. 如图,一座堤坝的横截面是梯形,根据图中给出的数据,求坝高和坝底宽(精确到0.1m)参考数据: 1.414, 1.732

四、解答题
-
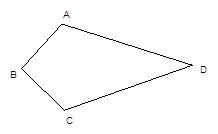
21. (A类)已知如图,四边形ABCD中,AB=BC,AD=CD,求证:∠A=∠ C.
(B类)已知如图,四边形ABCD中,AB=BC,∠A=∠C,求证:AD=CD.
五、解答题
-
22. 从称许到南京可乘列车A与列车B,已知徐州至南京里程约为350km,A与B车的平均速度之比为10∶7,A车的行驶时间比B车的少1h,那么两车的平均速度分别为多少?23. 小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:
项目
月功能费
基本话费
长途话费
短信费
金额/元
5

 (1)、 该月小王手机话费共有多少元?
(1)、 该月小王手机话费共有多少元?
(2)、扇形统计图中,表示短信费的扇形的圆心角为多少度?
(3)、 请将表格补充完整;
(4)、请将条形统计图补充完整.
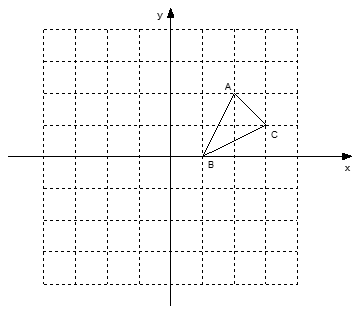
24. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)①画出△ABC关于x轴对称的△A1B1C1 ,
②画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2 ,
③△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;
④△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.
六、解答题
-
25. 为缓解油价上涨给出租车待业带来的成本压力,某巿自2018年11月17日起,调整出租车运价,调整方案见下列表格及图像(其中a, b,c为常数)
行驶路程
收费标准
调价前
调价后
不超过3km的部分
起步价6元
起步价a 元
超过3km不超出6km的部分
每公里2.1元
每公里b元
超出6km的部分
每公里c元
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
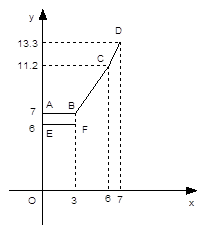 (1)、填空:a= , b= , c=.(2)、写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.(3)、函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义,若不存在请说明理由.26. 已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断
(1)、填空:a= , b= , c=.(2)、写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.(3)、函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义,若不存在请说明理由.26. 已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断① OA=OC ② AB=CD ③ ∠BAD=∠DCB ④ AD∥BC
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
(1)、构造一个真命题,画图并给出证明;
(2)、构造一个假命题,举反例加以说明.七、解答题
-
27. 已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5)
(1)、求该函数的关系式;(2)、求该函数图象与坐标轴的交点坐标;(3)、将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△O A′B′的面积.28. 如图1,一副直角三角板满足AB=BC,AC=DE,∠ABC=∠DEF=90°,∠EDF=30°【操作】将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上,再将三角板DEF绕点E旋转,并使边DE与边AB交于点P,边EF与边BC于点Q

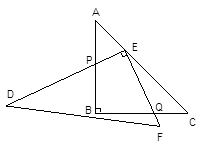
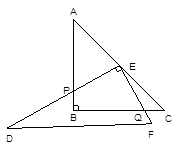 (1)、【探究一】在旋转过程中,
(1)、【探究一】在旋转过程中,①如图2,当 时,EP与EQ满足怎样的数量关系?并给出证明.
②如图3,当 时E P与EQ满足怎样的数量关系?,并说明理由.
③根据你对(1)、(2)的探究结果,试写出当 时,EP与EQ满足的数量关系式
为 , 其中 的取值范围是(直接写出结论,不必证明)
(2)、【探究二】若 且AC=30cm,连续PQ,设△EPQ的面积为S(cm2),在旋转过程中:①S是否存在最大值或最小值?若存在,求出最大值或最小值,若不存在,说明理由.
②随着S取不同的值,对应△EPQ的个数有哪些变化?不出相应S值的取值范围.
-